В работе описываются постановки задач о собственных и вынужденных колебаниях. Рассматриваются колебания механических систем, состоящих из абсолютно жестких тел, соединенных между собой безмассовыми вязкоупругими элементами.
Введение. Вопросы использования затухание динамических вязкоупругих систем с двумя степенями свободы, при всей изученности проблемы [1,2], редко рассматриваются в научной литературе. Вместе с тем, задачи защиты объекта в виде твердого тела на двух упругих опорах имеют значение для инженерной практики, поскольку системы «балочного» типа достаточно широко используются в транспортной динамике [3,4,5,6].
Постановка задачи. Общие положения. Рассмотрим линейную механическую систему с n степенями свободы, которая колеблется относительно устойчивой равновесной формы [1]. Движение системы опишем в обобщенных перемещениях 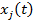 , которые равны нулю в положении равновесия. Тогда потенциальную энергию V можно выразить через эти перемещения, как квадратичную форму, а кинетическую энергию Т и функцию рассеяния D представить квадратичными формами обобщенных скоростей
, которые равны нулю в положении равновесия. Тогда потенциальную энергию V можно выразить через эти перемещения, как квадратичную форму, а кинетическую энергию Т и функцию рассеяния D представить квадратичными формами обобщенных скоростей 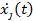 . Используя уравнения Лагранжа, получаем уравнения движения
. Используя уравнения Лагранжа, получаем уравнения движения
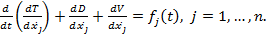 (1)
(1)
Обобщенная внешняя сила 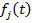 для каждой координаты может быть активной силой или силой, создаваемой заданным движением координат. Система (1) записывается в матричном виде относительно матрицы — столбца
для каждой координаты может быть активной силой или силой, создаваемой заданным движением координат. Система (1) записывается в матричном виде относительно матрицы — столбца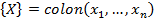 следующим образом:
следующим образом:
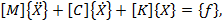 (2)
(2)
где матрица инерции [M], матрица демпфирования [С] и матрица жесткости [К] являются симметричными матрицами n-го порядка. Возмущение описывается посредством матрицы столбца 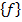 . Физический смысл коэффициентов матриц таков:
. Физический смысл коэффициентов матриц таков: 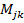 - составляющая количества движения по j при единичной скорости по
- составляющая количества движения по j при единичной скорости по 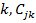 -демпфирующая сила по j при единичной скорости по
-демпфирующая сила по j при единичной скорости по 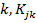 — упругая сила по j, обусловленная единичным перемещением по k.
— упругая сила по j, обусловленная единичным перемещением по k.
Установившиеся периодические колебания — это колебания, форма волны которых есть периодическая функция времени. Их можно представить как сумму тригонометрических функций с соизмеримыми частотами. Например, для колебаний, выраженных через ускорение
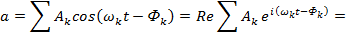
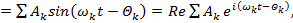 (3)
(3)
где 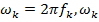 - угловая частота,
- угловая частота, 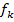 - соответствующая частота. Если все
- соответствующая частота. Если все 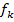 кратны какой-то основной частоте, то результирующая форма волны периодически повторяется. В противном случае она является квазипериодической или почти периодической. Комплексная экспоненциальная функция используется для теоретических анализов вместо тригонометрических функций отчасти потому, что ее производная по времени проще и введение комплексных чисел дает простой способ выражения изменения фаз и амплитуд колебаний. По стандартному фундаментальному методу определения амплитуд, когда резонансы комплектующего оборудования известны, сначала вычисляют отношения реакции к возбуждению в зависимости от частоты или измеряют их. Исходя из предположения о линейности, каждая синусоида может быть умножена на постоянное число и мгновенные характеристики на различных частотах могут быть суммированы. Отношение характеристики к возбуждению часто выражается как комплексное число, содержащее информацию о сдвиге фаз. Если характеристика и возбуждение представлены в одних и тех же единицах (например, как ускорение), то это отношение известно под названием способность передаваться. Если характеристика представляет собой движение (или, точнее скорость), а возбуждением является сила, то оно (отношение) называется подвижностью; в обратной ситуации — механическим импедансом. Если в точках необходимой характеристикой и точка возбуждения не совпадают, то более точными терминами будут подвижность переноса и сопротивление переноса. Ускорение получают умножая скорость на
кратны какой-то основной частоте, то результирующая форма волны периодически повторяется. В противном случае она является квазипериодической или почти периодической. Комплексная экспоненциальная функция используется для теоретических анализов вместо тригонометрических функций отчасти потому, что ее производная по времени проще и введение комплексных чисел дает простой способ выражения изменения фаз и амплитуд колебаний. По стандартному фундаментальному методу определения амплитуд, когда резонансы комплектующего оборудования известны, сначала вычисляют отношения реакции к возбуждению в зависимости от частоты или измеряют их. Исходя из предположения о линейности, каждая синусоида может быть умножена на постоянное число и мгновенные характеристики на различных частотах могут быть суммированы. Отношение характеристики к возбуждению часто выражается как комплексное число, содержащее информацию о сдвиге фаз. Если характеристика и возбуждение представлены в одних и тех же единицах (например, как ускорение), то это отношение известно под названием способность передаваться. Если характеристика представляет собой движение (или, точнее скорость), а возбуждением является сила, то оно (отношение) называется подвижностью; в обратной ситуации — механическим импедансом. Если в точках необходимой характеристикой и точка возбуждения не совпадают, то более точными терминами будут подвижность переноса и сопротивление переноса. Ускорение получают умножая скорость на 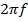 в соответствии с формулами для дифференцирования или на
в соответствии с формулами для дифференцирования или на 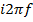 — при использовании комплексных обозначений. Мнимое число i выражает расхождение по фазе, равное 900. Установившиеся колебания представляют собой условное математическое понятие. Если Ak, Фk и Θk являются медленно меняющимися функциями времени, то функции вида (3) описывают квазипериодические колебания (сумму квазисинусоид). Для описания периодических колебаний рассматриваются только величины
— при использовании комплексных обозначений. Мнимое число i выражает расхождение по фазе, равное 900. Установившиеся колебания представляют собой условное математическое понятие. Если Ak, Фk и Θk являются медленно меняющимися функциями времени, то функции вида (3) описывают квазипериодические колебания (сумму квазисинусоид). Для описания периодических колебаний рассматриваются только величины 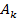 или соответствующие среднеквадратичные значения. Фазовые углы
или соответствующие среднеквадратичные значения. Фазовые углы 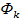 или
или 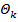 не учитываются. Однако мгновенные ускорения складываются арифметически, а величины синусоид при такой же частоте по правилам действия над векторами. Разность фаз теоретически имеет большое значение при анализе механических систем, а практически служит признаком резонанса, когда резонансные частоты определяются экспериментальным путем. Вблизи средней частоты фаза характеристики изменяется быстрее, чем величина частоты. Если матрица возбуждения
не учитываются. Однако мгновенные ускорения складываются арифметически, а величины синусоид при такой же частоте по правилам действия над векторами. Разность фаз теоретически имеет большое значение при анализе механических систем, а практически служит признаком резонанса, когда резонансные частоты определяются экспериментальным путем. Вблизи средней частоты фаза характеристики изменяется быстрее, чем величина частоты. Если матрица возбуждения 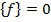 , то уравнение (2) описывает свободные колебания системы, а если
, то уравнение (2) описывает свободные колебания системы, а если 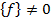 — то вынужденные.
— то вынужденные.
Свободные колебания диссипативных систем. Рассмотрим линейную диссипативную систему, движение которой описывается матрицами [М], [С] и [К]. Решение уравнения (2) можно найти в виде [7]
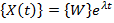 (4)
(4)
где λ– комплексное число, W- комплексная числовая матрица — столбец. Числа λ называют характеристическими показателями, а числа iλ (или — iλ) — комплексными частотами. Характеристические показатели должны быть корнями характеристического уравнения
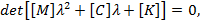 (5)
(5)
или в развернутом виде:
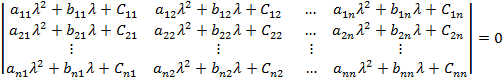 .
.
Система с n степенями свободы имеет 2n характеристических показателей 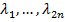 . Если все характеристические показатели суть простые корни уравнения (5), то общее решение уравнения (2) будет равно сумме 2n частных решений вида (4)
. Если все характеристические показатели суть простые корни уравнения (5), то общее решение уравнения (2) будет равно сумме 2n частных решений вида (4)
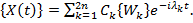 (6)
(6)
Здесь 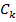 – произвольные комплексные постоянные, а
– произвольные комплексные постоянные, а 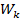 – числовые матрицы — столбцы. Представим характеристические показатели в виде
– числовые матрицы — столбцы. Представим характеристические показатели в виде
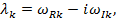
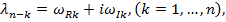 (7)
(7)
где 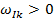 и
и 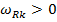 – действительные числа, называемые коэффициентами демпфирования и собственными частотами демпфированной системы соответственно. Если
– действительные числа, называемые коэффициентами демпфирования и собственными частотами демпфированной системы соответственно. Если 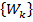 и
и 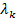 удовлетворяют уравнению (5), то комплексно сопряженные
удовлетворяют уравнению (5), то комплексно сопряженные 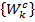 и
и 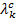 также ему удовлетворяют. Когда демпфирование отсутствует, все корни лежат на мнимой оси. При демпфировании корни находятся около мнимой оси. Соответствующие 2n собственные векторы удовлетворяют условиям ортогональности:
также ему удовлетворяют. Когда демпфирование отсутствует, все корни лежат на мнимой оси. При демпфировании корни находятся около мнимой оси. Соответствующие 2n собственные векторы удовлетворяют условиям ортогональности:
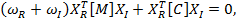
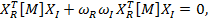 (8)
(8)
где индекс Т обозначает транспонирование. Каждый раз, когда 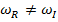 , условия ортогональности можно сделать справедливыми для кратных корней путем соответствующего выбора собственных векторов, связанных с кратным корнем.
, условия ортогональности можно сделать справедливыми для кратных корней путем соответствующего выбора собственных векторов, связанных с кратным корнем.
Характеристики демпфирования. Коэффициент демпфирования 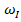 , задаваемой формулой (7) на первой части, имеет размерность
, задаваемой формулой (7) на первой части, имеет размерность 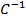 . За безразмерную характеристику демпфирования может быть принята одна из следующих величин:
. За безразмерную характеристику демпфирования может быть принята одна из следующих величин:
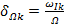 - относительный коэффициент затухания;
- относительный коэффициент затухания;
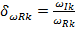 - относительный частотный коэффициент затухания;
- относительный частотный коэффициент затухания;
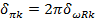 - логарифмический декремент затухания,
- логарифмический декремент затухания,
а также декремент затухания, равный отношению двух последовательных амплитуд колебаний с частотой 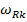 :
:
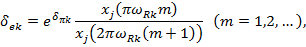
где 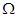 некоторая базисная (масштабная) частота. Если коэффициент затухания
некоторая базисная (масштабная) частота. Если коэффициент затухания 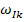 положителен, то параметры
положителен, то параметры 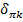 и
и 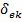 называются инкрементами возрастания колебаний. Связь между коэффициентом затухания
называются инкрементами возрастания колебаний. Связь между коэффициентом затухания 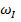 и амплитудой колебаний можно записать в виде:
и амплитудой колебаний можно записать в виде:
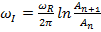 .
.
Задача нахождения комплексных собственных значений. При наличии симметричных матриц инерции, демпфирования и жесткости [М], [С] и [К] задача состоит в определении комплексных собственных значений 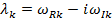 и комплексных собственных векторов
и комплексных собственных векторов 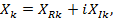 которые удовлетворяют уравнению (5). Эта задача значительно труднее и менее изучена, чем задача о вещественных собственных значениях уравнения (5). Для консервативной системы все характеристические показатели чисто мнимые (рис.1, а) и равны с точностью до множителя +i собственным частотам системы. Все частные решения являются периодическими функциями времени, а движение в общем случае стационарным (почти периодическим).
которые удовлетворяют уравнению (5). Эта задача значительно труднее и менее изучена, чем задача о вещественных собственных значениях уравнения (5). Для консервативной системы все характеристические показатели чисто мнимые (рис.1, а) и равны с точностью до множителя +i собственным частотам системы. Все частные решения являются периодическими функциями времени, а движение в общем случае стационарным (почти периодическим).
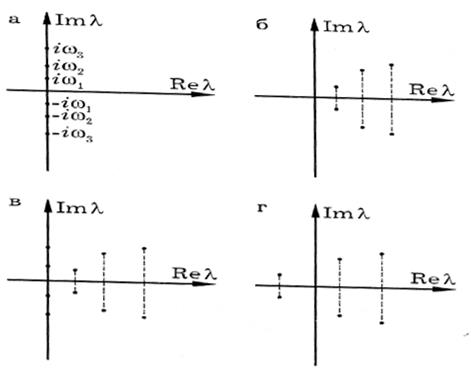
Рис. 1. Расположение характеристических показателей для систем: а — консервативной, б — с полной диссипацией, в — с неполной диссипацией, г — с отрицательной диссипацией
Если система диссипативная и обладает полной диссипацией, то все характеристические показатели лежат в нижней полуплоскости комплексной переменной (рис.1, б). Все частные решения — затухающие функции и, следовательно, общее решение — затухающая функция времени. Если система обладает неполной диссипацией, то часть ее показателей лежит в левой полуплоскости, а часть — на мнимой оси. Среди частных решений содержатся периодические, отвечающие недемпфированным степеням свободы. Если система обладает отрицательной диссипацией, то среди характеристических показателей можно найти такие, действительные части которых отрицательны (рис.1, г). Соответствующие частные и общие решения будут неограниченно возрастающими во времени функциями.
Демпфирование вынужденных колебаний. В стационарной задаче вектор-функция 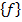 изменяется по гармоническому закону
изменяется по гармоническому закону 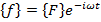 с заданной частотой и амплитудой
с заданной частотой и амплитудой 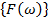 . Начальные условия не ставятся [3]. Вместо них требуется выполнение условия периодичности решения с той же частотой
. Начальные условия не ставятся [3]. Вместо них требуется выполнение условия периодичности решения с той же частотой 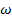 :
: 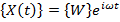 . В результате получаем систему алгебраических уравнений относительно комплексной компоненты искомого вектора
. В результате получаем систему алгебраических уравнений относительно комплексной компоненты искомого вектора 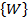 :
:
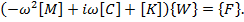 (9)
(9)
Систему (9) с комплексными коэффициентами можно решить, например, методом Гаусса.
Заключение. Предварительная оценка динамических свойств механических систем с N- степенями свободы, прикрепляемом через сочленение (или шарнир) показывает возможность изменения достаточно широкого спектра изменения частотных характеристик.
Литература:
1. Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. Ташкент: Фан, 1992. 250с.
2. Сафаров И. И., Тошев Н. Н. Установившиеся линейные колебания структурно-неоднородной виязкоупругой системы с несколькими степенями свободы. Изв.АН УзССР сер. техн. наук. 1988, № 3. С.37–40.
3. Коренев С. В. Динамические гасители колебаний. Теория и технические приложения. / Б. Г. Коренев, П. М. Резников. — М.: Наука, 1963. — 535 с.
4. Елисеев С. В., Нерубенко Г. П. Динамические гасители колебаний. — Новосибирск.: Наука. 1982. — 182 с.
5. Карамышкин В. В. Динамические гасители колебаний. — Л.: Машиностроение. 1988. — 108 с.
6. Ротенберг Р. В. Подвеска автомобиля. / Р. В. Ротенберг — М.: Машиностроение. 1972.
7. Сафаров И. И., Хусанов Д. Х. Вынужденные нелинейные виязкоупругой системы с конечным числом степеней свободы. Докл. АН УзССР, 1984, № 3. С.19–21.







