Вычисление «неберущихся» интегралов с помощью электронных таблиц Microsoft Excel

Сегодня умение пользоваться компьютером — насущная необходимость полноценного получения знаний для студента. Предлагая студентам ту или иную задачу, мы, прежде всего, учитываем наличие знаний по данному вопросу.

Рассмотрим пример урока по теме: Вычисление «неберущихся» интегралов с помощью электронных таблиц Microsoft Excel. Цели урока:

1.      Познакомить учащихся с методами приближённого вычисления определённого интеграла.

2.      Показать возможность применения электронных таблиц к приближённому вычислению определённых интегралов.

Задача учителя состоит в том, чтобы создать проблемную ситуацию, направить студентов на ее решение, организовать поиск решения. Для этого с учащимися необходимо повторить основные формулы интегрирования, сущность изученных методов интегрирования, геометрический смысл определённого интеграла.

При вычислении производной, мы используем таблицу производных и правила дифференцирования. Результат этих операций приводит к тому, что производная любой элементарной функции снова является элементарной функцией.

В некоторых случаях встречаются определённые интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, иногда приходится иметь дело с определёнными интегралами, сами подынтегральные функции не являются элементарными, то есть функция задается графиком или таблицей полученных значений. Поэтому мы во многих случаях не можем найти точное значение определенного интеграла по формуле Ньютона-Лейбница. Трудность операции интегрирования ещё состоит в том, что для неё нет универсального правила нахождения первообразных.

В науке и её приложениях в технике, экономике и других дисциплинах применяются многие неэлементарные функции; часто их называют специальными. К специальным функциям относятся и многие первообразные для элементарных функций, причём часто не столь уж «сложной» структуры. Интегралы, выражающиеся через такие первообразные, называются неберущимися. Итак, интеграл 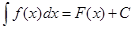 не берётся, если функция  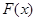не является элементарной. Можно показать, что интегралы от некоторых элементарных функций уже не являются элементарными функциями. Примерами таких интегралов могут служить следующие интегралы:

1. 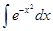                 – интеграл Пуассона. Функция 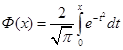называется функцией Лапласа или интегралом вероятности. Она широко применяется в теории вероятностей, физике, математической и прикладной статистике и других разделах науки и её приложений. Для вычисления значений функции Лапласа составлены таблицы, имеющиеся во многих учебниках, задачниках и справочниках по теории вероятностей и статистике. Интеграл Пуассона широко применяется в теории вероятности;

2. 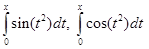                 – интегралы Френеля;

3. 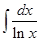                 – интегральный логарифм;

4. 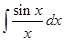                 – интегральный синус;

5. 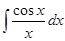                 – интегральный косинус;

6. 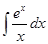                 – интегральная экспонента.

Когда не удаётся выразить интеграл в замкнутой форме, или полученная формула сложна, или подынтегральная функция задана таблично, используют численное интегрирование, которое основывается на том, что интеграл представляется в виде предела интегральной суммы (суммы площадей), и позволяют определить эту сумму с приемлемой точностью.

Существуют различные методы для реализации этой проблемы, но наиболее простые:

-        методы прямоугольников (левых, правых и средних прямоугольников);

-        метод трапеций;

-        метод парабол.

Метод прямоугольников — это простой и вместе с тем наиболее грубый метод приближенного интегрирования. Геометрическая интерпретация этого метода выглядит следующим образом:

 

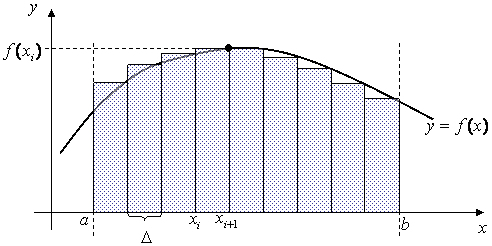
Построим блок-схему решения метода прямоугольников:

 

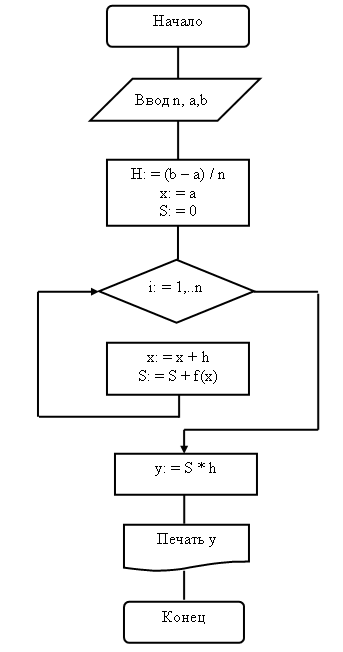
Преподаватель создает проблемную ситуацию, состоящую в нахождении интеграла 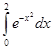. Студенты делают вывод о том, что в этом случае не применимы изученные методы и признают ситуацию проблемной.

Рассмотрим метод «Приближённое вычисление определенных интегралов по формуле правых прямоугольников» на примере интеграла Пуассона, заключённого на отрезке [0;2]., т. е. 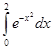и попробуем его приближенно вычислить с помощью электронной таблицы Excel, результат вычислений проанализируем. Для этого вначале отрезок [0;2] разобьём на 20 равных частей, т. е.  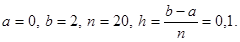Создадим таблицу значений 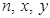, где 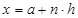. Воспользуемся методом правых прямоугольников: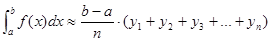

В электронной таблице создадим таблицы и введем формулы, используя автозаполнение:

 

Построим криволинейную трапецию, ограниченной данной функцией, отрезком [0;2] и осью ОХ, для этого используем вставку диаграммы с областями:

 

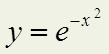
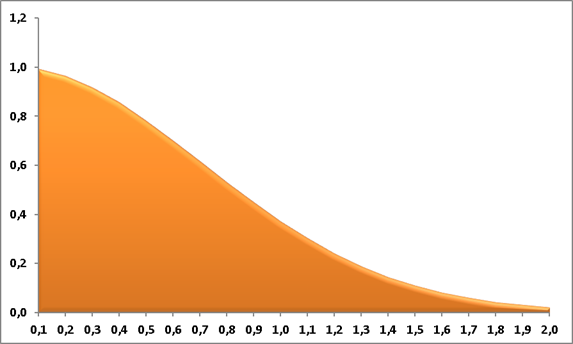
За точное значение примем результат вычисления с помощью математического процессора MathCAD:

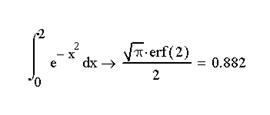
Этот же результат получим с помощью интернет-сервисов на сайте http://www.wolframalpha.com/

 

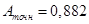. Вычислим абсолютную и относительную погрешность:

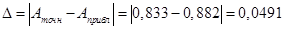
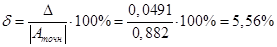
Изменим число разбиений отрезка [0;2] на 200 равных частей. Проанализируем точность вычисления интеграла. Для этого изменим данную таблицу.

 

Сравнивая полученные результаты таблиц, наглядно видно, что во второй таблице точность вычисления данного интеграла выше, чем в первом случае, относительная погрешность во втором случае составляет менее 1 %, т. е. 0,55 %.

Контрольные вопросы.

1.      Как уменьшить погрешность нахождения интеграла в методе прямоугольников?

2.      В каких случаях метод прямоугольников находит применение?

3.      Можно ли получить методами прямоугольников точное значение интеграла?

Заключение и выводы.

Таким образом, очевидно, что методом прямоугольников при вычислении определенных интегралов не дает нам точного значения, а только приближенное. Следовательно, при увеличении числа разбиений (приуменьшения шага), точность вычислений увеличивается, т. к. уменьшается относительная погрешность. Если точность вычисления интеграла задана, то можно определить, на сколько частей нужно разбить отрезок.

 

Литература:

 

1.      http://www.wolframalpha.com/

2.      Алгебра и начала математического анализа. 11 класс. Виленкин Н. Я.

3.      Информатика и информационные технологии. Учебник для 10–11 классов. Угринович Н. Д.