Рассматривается операторная матрица в прямой сумме нолчастичного, одночастичного и двухчастичного подпространств фоковского пространства. Изучаются некоторые свойства, в основном связанные с числами собственных значений, соответствующих дополнении Шура и приведены их следствия.
Ключевые слова: операторная матрица, первое и второе дополнение Шура, пространство Фока, существенный и дискретные спектры.
Блочно-операторная матрица — это матрица элементы которой являются линейными операторами в банаховым или гильбертовом пространстве [1]. Пусть 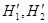 и
и 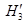 -три гильбертовы пространства и
-три гильбертовы пространства и 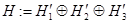 . Тогда известно, что всякий линейный ограниченный оператор
. Тогда известно, что всякий линейный ограниченный оператор 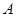 , действующий в
, действующий в 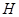 всегда представляется как
всегда представляется как 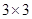 блочно-операторная матрица
блочно-операторная матрица
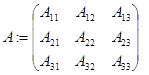 (1)
(1)
с линейными ограниченными операторами 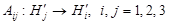 . При этом оператор
. При этом оператор 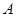 является самосопряженным тогда и только тогда, когда
является самосопряженным тогда и только тогда, когда
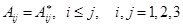
(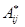 сопряженный оператор к
сопряженный оператор к 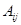 ).
).
Обозначим через 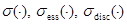 и
и 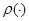 , соответственно, спектр, существенный спектр, дискретный спектр и резольвентное множества ограниченного самосопряженного оператора.
, соответственно, спектр, существенный спектр, дискретный спектр и резольвентное множества ограниченного самосопряженного оператора.
Далее, пространство 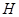 представим в виде ортогональной суммы гильбертовых пространств
представим в виде ортогональной суммы гильбертовых пространств 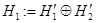 и
и 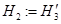 . Положим
. Положим
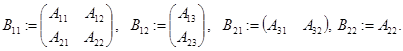
Очевидно, что 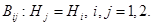 Тогда оператор
Тогда оператор 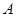 действующий в
действующий в 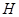 относительно представление
относительно представление 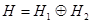 записывается как блочно-операторная матрица следующего вида:
записывается как блочно-операторная матрица следующего вида:
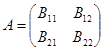 (2)
(2)
Пусть 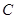 - множество комплексных чисел и
- множество комплексных чисел и 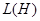 - пространство линейных ограниченных операторов в гильбертовом пространстве
- пространство линейных ограниченных операторов в гильбертовом пространстве 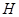 . Следующие операторы
. Следующие операторы
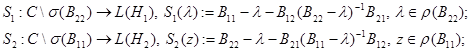
называются дополнениями Шура соответствующий блочно-операторной матрицы 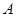 , определенный по формуле (2) и они играют важную роль в спектральном анализе этой матрицы. Видно, что дополнение Шура являются операторно-значные регулярные функции определенные вне спектров операторов
, определенный по формуле (2) и они играют важную роль в спектральном анализе этой матрицы. Видно, что дополнение Шура являются операторно-значные регулярные функции определенные вне спектров операторов 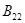 и
и 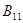 , соответственно.
, соответственно.
Дополнение Шура сначала использовано в теории матриц [2]. Термин «дополнение Шура» было введено в работе [3]. В бесконечномерных гильбертовых пространствах, дополнение Шура впервые изучена в известной работе М. Г. Крейна [4] о расширениях самосопряженных операторов. Исходя их применениях в теории матриц и численной линейной алгебры, дополнение Шура использованы во многих областях математики такие как статистика, электротехника, 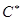 - алгебры [5] и теория математических систем [6].
- алгебры [5] и теория математических систем [6].
В теории ограниченных и неограниченных блочно-операторных матриц дополнение Шура является мощным инструментом при изучении спектра и различных спектральных свойств. Эти свойства впервые была исследованы в работах Р. Нагела [7,8].
Соотношение между спектральных свойств блочно-операторной матрицы 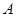 и дополнение Шура можно наблюдать из так называемой «факторизация Фробениуса-Шура», т. е.,
и дополнение Шура можно наблюдать из так называемой «факторизация Фробениуса-Шура», т. е.,
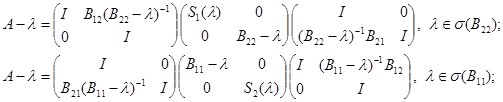
(см. например [1]). При этом 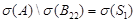 и
и 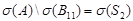 . Здесь для регулярной оператор-функции
. Здесь для регулярной оператор-функции 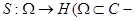 открытое множество) его спектр понимается как
открытое множество) его спектр понимается как
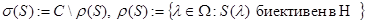 .
.
В работе [9] существенный спектр блочно-операторной матрицы определен в терминах дополнение Шура. Затем многие работы посвящены на этот объект. Для подробных изложений см. монографию [1].
Следует отметить, что включение 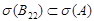 не всегда выполняется, а дополнение Шура
не всегда выполняется, а дополнение Шура 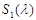 определена при
определена при 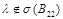 . В настоящей работы рассмотрим модель
. В настоящей работы рассмотрим модель 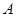 , возникающий в задачах статистической физики [10], квантовой теории поля [11] и физики твердого тела [12], который представляется как (1). При этом имеет место включение
, возникающий в задачах статистической физики [10], квантовой теории поля [11] и физики твердого тела [12], который представляется как (1). При этом имеет место включение 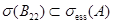 . Изучаются свойства оператор-функции
. Изучаются свойства оператор-функции 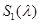 о спектре и приведены их следствия.
о спектре и приведены их следствия.
Пусть 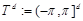
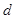 -мерный куб с соответствующим отождествлением противоположных граней,
-мерный куб с соответствующим отождествлением противоположных граней, 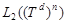 - гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
- гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 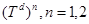 . Рассмотрим случай, когда
. Рассмотрим случай, когда 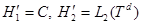 и
и 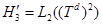 . Пространства
. Пространства 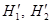 и
и 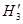 называются нольчастичным, одночастичным и двухчастичным подпространством стандартного фоковского пространства
называются нольчастичным, одночастичным и двухчастичным подпространством стандартного фоковского пространства 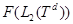 по
по 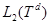 , соответственно, где
, соответственно, где
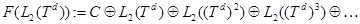 .
.
Всюду в работе будем рассматривать блочно-операторную матрицу 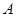 , определенную по формуле (1), со следующими матричными элементами
, определенную по формуле (1), со следующими матричными элементами
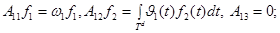
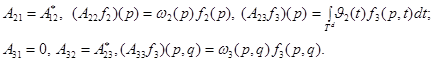
Здесь 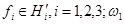 -фиксированное вещественное число;
-фиксированное вещественное число; 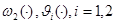 и
и 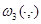 - вещественно-непрерывные функции на
- вещественно-непрерывные функции на 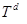 и
и 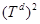 , соответственно. При этом
, соответственно. При этом
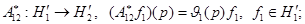
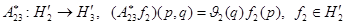 .
.
Можно легко проверить, что при этих предположениях блочно-операторная матрица 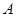 является ограниченным и самосопряженным оператором в
является ограниченным и самосопряженным оператором в 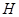 .
.
Операторы 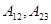 называются операторами уничтожения, а операторы
называются операторами уничтожения, а операторы 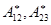 называются операторами рождения.
называются операторами рождения.
Простые вычисления показывают, что первое дополнение Шура 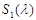 блочно-операторной матрицы
блочно-операторной матрицы 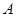 (действующее по формуле (2)) соответствующее разложению
(действующее по формуле (2)) соответствующее разложению 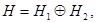 определяется следующим образом
определяется следующим образом
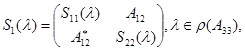
где
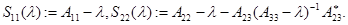
При каждом фиксированном 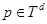 определим регулярную в
определим регулярную в 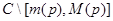 функцию
функцию
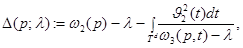
где числа 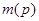 и
и 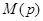 определяются следующим образом:
определяются следующим образом:
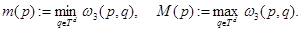
Тогда 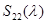 есть оператор умножения на функцию
есть оператор умножения на функцию 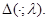 Следует отметить, что при каждом фиксированном
Следует отметить, что при каждом фиксированном 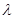 оператор типа (3) является оператором, носящим название обобщенной модели Фридрихса.
оператор типа (3) является оператором, носящим название обобщенной модели Фридрихса.
Пусть 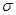 - замыкание множество точек
- замыкание множество точек 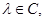 для которых уравнение
для которых уравнение 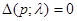 имеет решение хотя бы для одной
имеет решение хотя бы для одной 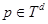 и
и
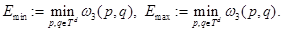
Тогда для существенного спектра оператора 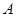 имеет место равенство
имеет место равенство
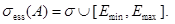
Из непрерывности функции 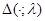 при
при 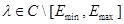 на компактном множестве
на компактном множестве 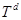 следует, что
следует, что 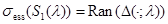 .
.
Следующие две свойства устанавливают связь между дискретным и существенным спектрами операторов 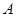 и
и 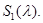
Свойства 1. Число 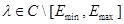 является собственным значением оператора
является собственным значением оператора 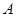 тогда и только тогда, когда оператор
тогда и только тогда, когда оператор 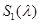 имеет собственное значение, равное нулю и их кратности совпадают.
имеет собственное значение, равное нулю и их кратности совпадают.
Свойства 2. Пусть 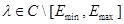 . Тогда
. Тогда 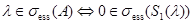 .
.
Из свойств 1 и 2 вытекает следующие
Следствие 1. Пусть 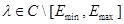 . Тогда
. Тогда 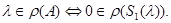
Следствие 2. Пусть 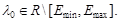 Если
Если 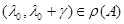 (соот.
(соот. 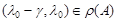 ) при некотором
) при некотором 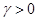 , то существует число
, то существует число 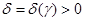 такое, что
такое, что 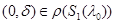 (соот.
(соот.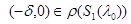 ).
).
Отметим, что при каждом фиксированном 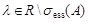 оператор
оператор 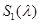 является самосопряженным. Через
является самосопряженным. Через 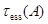 обозначим нижнюю грань существенного спектра оператора
обозначим нижнюю грань существенного спектра оператора 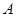 .
.
Свойства 3. При 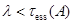 число собственных значений оператора
число собственных значений оператора 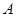 , с учетом кратности, меньших чем
, с учетом кратности, меньших чем 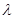 , равно число положительных собственных значений оператора
, равно число положительных собственных значений оператора 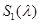 , с учетом кратности.
, с учетом кратности.
Литература:
1. C. Tretter. Spectral Theory of Block Operator Matrices and Applications. Imperial College Press, 2008.
2. I. Schur. Uber potenzreihen, die im innern des einheitskreises beschrankt sint. J. Reine Angew. Math., 147 (1917), 205–232.
3. E. V. Haynsworth. Determination of the inertia of a partitioned Hermitian matrix. Linear Algebra Appl., 1:1 (1968), 73–81.
4. М. Г. Крейн. Теория самосопряженных расширений полуограниченных эрмитовых операторов и ее приложения. Матем. сборник, 20 (1947), 365–404.
5. F. Zhang. The Schur complement and its applications. Vol. 4 of Numerical Methods and Algorithms. Springer, New York, 2005.
6. H. Bart, I. C. Gohberg, M. A. Kaashoek, A. C. V. Ran. Schur complements and state space realizations. Linear Algebra Appl., 399 (2005), 203–224.
7. R. Nagel. Well-posedness and positivity for systems of linear evolution equations. Confer. Sem. Mat. Univ. Bari, 203 (1985), 1–29.
8. R. Nagel. The spectrum of unbounded operator matrices with non-diagonal domain. J. Func. Anal., 89:2 (1990), 291–302.
9. F. V. Atkinson, H. Langer, R. Menniken, A. A. Shkalikov. The essential spectrum of some matrix operators. Math. Nachr., 167 (1994), 5–20.
10. В. А. Малышев, Р. А. Минлос. Кластеpные опеpатоpы. Тpуды семинаpа им. И. Г. Петpовского. Вып. 9 (1983), 63–80.
11. К. О. Фридрихс. Возмущение спектра операторов в гильбертовом пространстве. М.: Мир, 1969.
12. D. Mattis. The few-body problem on a lattice. Rev. Modern Phys., 58:2 (1986), 361–379.







