Проблемы теории управления в технических системах, в частности математические, программные, методологические основы и методы построения АСУ, рассмотрены в работах Бусленко Н. П., Растригина Л. А., Ивахненко А. Г., Абчука В. А., Васильева Ю. Н., Меерова М. В., Кабулова В. К., Камилова М. М., Набиева О. М., Алиева Э. М., Назирова Ш. А., Эгамбердиева Х. З., Ражабова Б., Бекмурадова Т. Ф., Фазылова Ш. Х. и других ученых.
Основные принципы автоматизированных систем управления разработкой крупных газовых месторождений рассмотрены в работах Маскета М., Чарного И. А., Лапука Б. Б., Закирова С. Н., Берщенского, Шмыгля П. Т., Коратаева Ю. П., Маргулова Р. Д., Щелкачева В. Н., Гусейн-заде М. А., Хантуша М. С., Требина Ф. А., в частности моделированию процесса фильтрации газа применительно к разработке нефтегазовых месторождений Республики Узбекистан, а также разработке к ним эффективных вычислительных алгоритмов и их реализации на больших электронных вычислительных машинах посвящены работы Кабулова В.К, Абуталиева Э. Б., Абуталиева Ф. Б., Мухитдинова Н., Садуллаева Р., Алимова И., Назарова Н. С., Назарова У. С., Арсланова А., Джанибекова Ч., Сиддикова А., Мукимова Н., Бегматова А., Валиева Т. и других ученых. [1,2]
Из приведенного анализа следует, что сделано очень много работы по направлению настоящей работы. Однако анализ показал, что в республике недостаточно пакетов прикладных программ, созданных на объектно-ориентированных языках для современных компьютеров на основе эффективных алгоритмов и методов.
Настоящее исследование посвящено изысканию возможностей применения совокупности моделей функционирования систем для оперативного анализа, прогнозирования и управления показателями эксплуатации газового месторождения как объекта управления. Таким образом, задача оптимального управления и прогнозирования изменений параметров разработки газовых месторождений весьма актуальна для народного хозяйства республики.
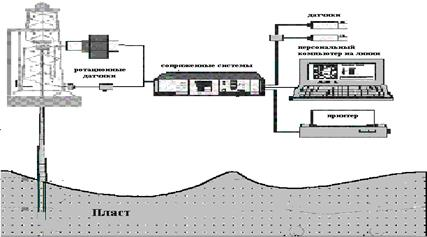
Рис.1. Глобальная техническая схема управления процессом разработки газовых месторождений
Исследуемые объекты добычи газа по своей структуре и технико-технологическим свойствам относятся к классу сложных систем (рис.1). Основными факторами, характеризующими эти объекты, являются многомерность, многосвязанность и многоплановость.
Также в этой статье рассматривается управление фильтрационными системами с использованием математических моделей. Задачи оптимального управления разработкой нефтегазовых месторождений ставятся на основании математических моделей управления процессом, описывающих гидродинамические процессы в пласте. В настоящее время разработано множество математических моделей управления процессом, методов, алгоритмов и программных средств, которые по мере их подготовленности вошли в различные математические и информационные обеспечения разработки нефтяных и газовых месторождений.
В работе исследуется минимизация функционала J(u) при помощи выбора оптимального вычислительного алгоритма в смысле реального машинного времени и подбора дебитов скважин:
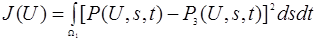 ,
,
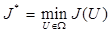 ,
, 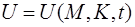 (1)
(1)
при ограничениях 0≤Qi,j(t) ≤Qi,jmax, 0<Pi,j(t) ≤P0, 0<Mi,j≤1,
где P3(U,s,t) — желаемое распределение давления в газоносной области в заданный момент времени; P(U,s,t) — расчетное значение давления в тех же точках; Q-дебит скважины; М — коэффициент пористости.
Выбирается такое Р(U,s,t), которое дает минимум для J.
Решая данную задачу, т. е. задавая желаемое распределение значения давления в заданной области, мы можем оптимально управлять движением газа в пористой среде.
Дифференциальные уравнения неустановившейся фильтрации реального газа в реальной, неоднородной по коллекторским свойствам пористой среде (т. е. проницаемость и мощность пласта зависят от координат абсциссы и ординаты), имеют вид
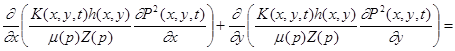
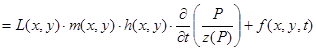 . (2)
. (2)
Здесь K(x,y,t), h(x,y), m(x,y), L(x,y) — соответственно проницаемость, мощность, пористость и газонасыщенность пласта, P(x,y,t), z(p), 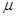 (p) — давление, сверхсжимаемость, вязкость газа.
(p) — давление, сверхсжимаемость, вязкость газа.
Рассмотрим математическую формулировку возможных начальных и краевых условий, исходя из физического смысла задачи. При этом отметим, что кроме граничных условий, необходимо задать начальное условие, характеризующее распределение пластового давления до ввода в эксплуатацию системы скважин:
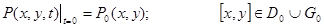 . (3)
. (3)
Рассмотрим частные случаи заданных краевых условий. Нам известно, что граничные условия можно задавать в общем виде:
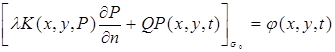 . (4)
. (4)
Если 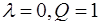 , тогда получаем первое граничное условие, в противном случае — второе граничное условие. Условия могут быть заданы в комбинированном виде.
, тогда получаем первое граничное условие, в противном случае — второе граничное условие. Условия могут быть заданы в комбинированном виде.
Предположим, известны коллекторские свойства пласта, начальное пластовое давление, отборы газа из скважин по времени, состав газа, температура пласта, расположение скважин, геометрия пласта. Кроме этого, предположим, что пласт имеет непроницаемую границу. При этих условиях двухмерная нестационарная фильтрация газа в пористой среде описывается в виде (2) краевой задачи в заданных начальных (3) и граничных условиях (4). В правой части уравнения (2) вместо f(x,y,t) задается дебит:
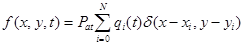 , (х,у)
, (х,у)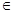 D0, t>t0, (5)
D0, t>t0, (5)
где qi(t), (xi,yi), N — соответственно отборы, координаты и количество скважин; Рат — атмосферное давление, D0 — область фильтрации;P0(x,y) — начальное распределение давления, 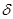 (x,y) — двухмерная функция Дирака. [3,4]
(x,y) — двухмерная функция Дирака. [3,4]
Наряду с сформулированной задачей в практике и теории рассматривается и следующая задача.
Заданы все перечисленные данные и, кроме дебитов скважин, фактические давления на скважинах. Требуется определить поля давления P(x,y,t). Решение этой задачи может быть использовано для построения карты изобар для уточнения параметров пласта. Задача формулируется следующим образом.
Требуется определить функцию давления P(x,y,t) в области D из уравнения (2) при заданных начальных и граничных условиях. Вместо правой части уравнения задается давление в виде
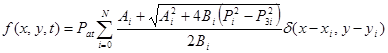 , (х,у)
, (х,у)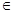 D0, t>t0. (6)
D0, t>t0. (6)
Здесь Pi, P3i — фактическое пластовое и забойное давления на скважинах, Ai,Bi — коэффициенты фильтрационных сопротивлений; i — номер скважины, G0-граница области фильтрации, D=D0+G0.
Таким образом, решая уравнение (2) с различными граничными, а также внутренними условиями, получаем несколько математических моделей исследуемой задачи. Кроме того, в работе при различных физических предположениях приведены упрощенные математические модели этих задач. [5]
В этой работе приведена математическая модель, рассматривается выбор метода решения на основе вычислительного эксперимента, обоснованы устойчивость, погрешность, точность и достоверность методов на тестовых примерах. В основном определяются эффективные вычислительные алгоритмы для задачи (2)-(6).
Для построения вычислительного алгоритма по решению уравнений (2)-(6) и его разновидностей применены методы: переменных направлений, покомпонентного расщепления и локально-одномерный:
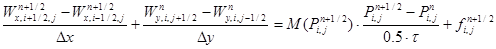 , (7)
, (7)
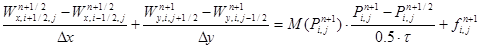 , (8)
, (8)
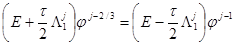 , (9)
, (9)
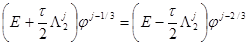 , (10)
, (10)
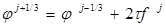 (11)
(11)
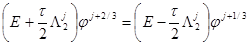 , (12)
, (12)
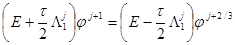 , (13)
, (13)
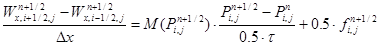 , (14)
, (14)
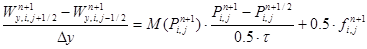 , (15)
, (15)
где 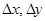 и
и 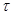 — шаги по координатным осям и времени;
— шаги по координатным осям и времени;
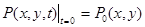 ,
, 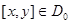 , (16)
, (16)
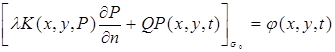 ; (17)
; (17)
здесь =0 и 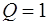 .
.
В формулах (7)-(17) применены сеточные аналоги задачи (2)-(6), в частности схема переменных направлений (7)-(8), схема покомпонентного расщепления (9–13) и локально — одномерная схема (14)-(15). Начальное и граничное условия учитываются в виде (16)-(17).
Вычислительный алгоритм приведен в таком порядке:
1. Замена дифференциального оператора некоторым разностным оператором. Формулирование разностного аналога для краевых условий и начальных данных.
2. Построение фиктивной области.
3. Переход к конечно — разностным уравнениям.
4. Построение реализационного алгоритма.
5. Анализ полученных результатов.
Для проверки достоверности вычислительного алгоритма и разработанного программного комплекса применен метод пробной функции.
Пусть пробная функция имеет вид 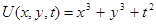 с постоянными коэффициентами const, M=1; K=1. Тогда, подставив функцию в уравнение, имеем f=6x+6y+2t с начальным условием
с постоянными коэффициентами const, M=1; K=1. Тогда, подставив функцию в уравнение, имеем f=6x+6y+2t с начальным условием 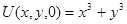 .
.
Для нашей задачи коэффициенты граничных условий следующие: 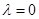 и
и 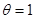 . Тогда первое граничное условие примет следующий вид:
. Тогда первое граничное условие примет следующий вид:
j (0,y,t)= y3+t2 при x=0, j (1,y,t)= 1+y3+t2 при x=1,
j (y,0,t)= x3+t2 при y=0, j (x,1,t)= x3+1+t2 при y=1.
При решении тестовой задачи для проверки результатов изменяем шаг по времени. На основе этих результатов составлен график, который показывает погрешность точного и приближенного решений (рис.2).
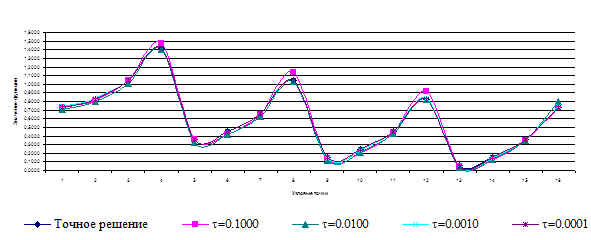
Рис. 2. Сравнительные результаты полученных результатов на основе метода переменных направлений
Из приведенных результатов видно, что если шаг по времени будет очень мал, тогда результат приближается к точному решению, а при больших временных шагах устойчивость нарушается.
Литература:
1. Абчук В. А. и др. Автоматизация управления. –М.: Радио и связь, 1984. –264 с.
2. Азиз Х., Сеттари Э. Математическое моделирование пластовых систем. –М.: Недра, 1982, -400 с
3. Олимов М. Алгоритм решения прикладных задач для обыкновенных дифференциальных уравнений четвертого порядка с методом дифференциальной прогонки [Текст] / М. Олимов, О. О. Жакбаров, Ф. С. Ирискулов // Молодой ученый. — 2015. — № 6. — С. 193–196.







