Гравитация – это преобладающая сила во Вселенной. Она проявляется и в малых и в больших масштабах. Гравитация нужна нам, чтоб оставаться на Земле, она нужна, чтоб мы могли бегать и прыгать. Например, горнолыжник использует её силу, чтоб спуститься с горы. Гравитация действует на все предметы 24 часа в сутки. Любой предмет падает под её действием на землю со скоростью 9,8 метра в секунду. Все что обладает массой во Вселенной, порождает тяготение. Гравитация способна творить, разрушать, сминать и управлять всей материей.
От силы тяжести ничто не может ускользнуть, и она действует на весьма удаленные предметы. Тяготение удерживает нашу солнечную систему в целостности. Этот космический «клей» способен удерживать даже целые галактики. Если взять два игральных кубика и разместить их в космосе на расстоянии 1 см, то через час они сойдутся.
Наше Солнце возникло из огромного газового облака, которое сжалось под действием силы тяжести. Подобным образом возникла и наша Земля, когда небольшие частицы скапливались и соединялись в большое тело.
Для гравитации очень важны масса и расстояние между объектами. Сила пропорциональна произведению двух масс, то есть количеству материи в объектах. Другими словами, чем больше тело, тем сильнее оно притягивает другие тела. Даже в скоплении Галактик все они движутся вокруг общего скопления масс.
Уже много веков человечество ищет пользу от такой неугасаемой силы, как гравитация. Галилео Галилей открыл понятие тяготения, а также определил, что тела с разной массой падают на Землю с одинаковой скоростью. Сэр Исаак Ньютон увидел падающее яблоко, и это перевернуло мир науки. Он понял что луна, которая летает вокруг Земли, тоже падает на нее. Но разве может Луна упасть? Ньютон при помощи пороховой пушки и математики взялся решать эту задачу. Это открытие опубликовано в книге «Принципы математики» в 1687 году. Если выстрелить из пушки с достаточной мощностью, то ядро не успеет упасть, а вылетит на орбиту и будет летать уже вокруг Земли. Уже в то время Ньютон смог рассчитать, что необходимая скорость для этого составит 28 000 км/ч. Вот почему Луна не падает на Землю, она летит с достаточной скоростью вращения. Так же и Земля вокруг Солнца летит в свободном падении, но не падает.
Как известно, в поле тяготения массивного центрального тела движение происходит по классическим траекториям — эллипсам, параболам и гиперболам.
Если использовать гравитацию планет и их спутников в качестве разгонных и тормозящих объектов, можно значительно сократить топливо космического аппарата (КА).
Прямолинейный полет от Земли к другой планете энергетически крайне невыгоден.
Минимальные затраты энергии на перелет между двумя круговыми орбитами обеспечиваются, когда траектория представляет собой «половинку» эллипса, касающегося исходной и конечной орбит.
При этом двигатель космического аппарата должен выдать всего два импульса: в перигее и апогее (если речь идет об околоземном пространстве) переходного эллипса.
Данная схема используется при выведении на геостационарную орбиту.
В межпланетных полетах задача несколько осложняется необходимостью учитывать притяжение Земли и планеты назначения соответственно на начальном конечном участках траектории.
Биэллиптические траектории оптимальны для перевода спутника между круговыми орбитами с разным наклонением.
В существующих исследованиях по использованию гравитационных маневров в целях экономии топлива космического аппарата (КА), преследуется цель выбора траектории захода и выхода КА на орбиту движения.
Этот факт естественно безусловен, однако используя незначительную часть их кинетической энергии планет можно разогнать или «тормознуть» КА.
Для этого необходимо рассчитать гравитационное поле вблизи каждой планеты и рассчитать координаты движения планет.
Вначале рассчитаем расстояние от Солнца нулевого потенциала φ0, где корабль попадает в поле планета.
Для этого приравняем силы гравитации Солнца и планеты:
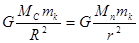, откуда следует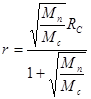 
Расчеты зоны действия гравитации планет проводим в электронных таблицах EXCEL Таблица 1.
 |
|
Планета |
Масса (о.е) |
Масса |
Расстояние (а .е) |
Расстояние (м) |
Сила (Н) |
Период |
Расстояние действия гравитации (км) |
|
|
Меркурий |
0,06 |
3,60E+23 |
0,39 |
5,85E+10 |
1,40E+22 |
0,24 |
0,000424 |
24809 |
|
Венера |
0,82 |
4,92E+24 |
0,72 |
1,08E+11 |
5,63E+22 |
0,61 |
0,001568 |
169126 |
|
Земля |
1 |
6,00E+24 |
1 |
1,50E+11 |
3,56E+22 |
1 |
0,001732 |
259358 |
|
Марс |
0,11 |
6,60E+23 |
1,52 |
2,28E+11 |
1,69E+21 |
1,88 |
0,000574 |
130901 |
|
Юпитер |
318 |
1,91E+27 |
5,2 |
7,80E+11 |
4,18E+23 |
11,86 |
0,030887 |
23369949 |
|
Сатурн |
95,2 |
5,71E+26 |
9,54 |
1,43E+12 |
3,72E+22 |
29,46 |
0,0169 |
23781575 |
|
Уран |
14,6 |
8,76E+25 |
19,19 |
2,88E+12 |
1,41E+21 |
84,02 |
0,006618 |
18925115 |
|
Нептун |
17,2 |
1,03E+26 |
30,07 |
4,51E+12 |
6,77E+20 |
164,78 |
0,007183 |
32169256 |
|
Плутон |
0,002 |
1,20E+22 |
39,52 |
5,93E+12 |
4,56E+16 |
247,7 |
0,000424 |
24809 |
|
|
|
2,68E+27 |
Максимальная сила на Солнце |
5,65E+23 |
|
|
|
|
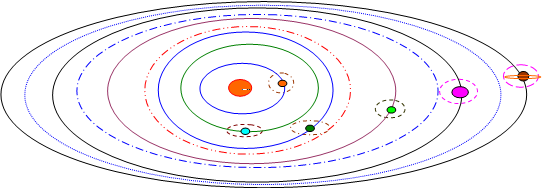
Рис. 1. Схема гравитационных полей Солнечной системы
Исходя из таблицы данных планет Солнечной системы, рассчитаем зону действия планет, где гравитации Солнца меньше гравитации планеты: Таблица 1.
На представленном рисунке «Схема гравитационных полей Солнечной системы», показаны эллиптические орбиты гравитационных полей планет.
Эллипсы вокруг Солнца показывают их годовые координаты, а эллипсы вокруг планет, их размеры в текущем состоянии.
Зная параметры планет, массы, радиусы их орбит, эксцентриситеты, периоды движения, а также скорости КА, можно рассчитать оптимальные траектории движения летательных аппаратов.
Космический аппарат может «выскочить из зоны действия планеты исходя из его эксцентриситета и кинетической энергии.
Расчет траектории Космического аппарата, необходимо проводить исходя из эксцентриситета траектории.
Согласно механики Ньютона и законов Кеплера, фокальное уравнение канонического сечения, для движения тела в поле гравитации, эксцентриситет движущего тела определится:
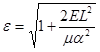
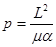
где ε- эксцентриситет
 |
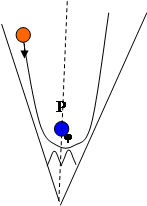Рис. 2. Потенциальные гравитационные поля планет Солнечной системы.
