Управление линейной динамической системой в условиях непараметрической неопределенности

Представленная статья посвящена теме управления объектами в условиях, когда имеющейся информации недостаточно для построения математической модели объекта в параметрическом виде. Предполагается, что исследователю известны лишь некоторые наиболее существенные характеристики, такие, к примеру, как линейность и стационарность. Имеется возможность наблюдать значения входных и выходных переменных. Такие условия, называемые условиями непараметрической неопределенности, являются довольно распространенными на практике, однако существующая теория посвящена в основном параметрическим методам идентификации и управления. Таким образом, существует потребность в совершенствовании и подробном изучении методов применимых в данном случае.

Будут рассмотрены некоторые из методов управления, для которых нет необходимости в отыскании параметрической модели. К ним относится широко распространенный и зарекомендовавший себя на практике ПИД-регулятор, и относительно новый для теории управления непараметрический регулятор. Кроме того, в данных регуляторах используется модель системы в непараметрическом виде, алгоритм построения которой так же будет описан далее. В частности в ПИД-регуляторе данная модель будет использована для настройки его коэффициентов.

Идентификация непараметрической модели.

Описание процессов, происходящих в линейных динамических системах, может быть осуществлено, если известен вид одной из следующих характеристик: дифференциального уравнения, передаточной функции, весовой или переходной характеристики. Ввиду того, что вид первых двух характеристик определить в предполагаемых условиях не представляется возможным, непараметрическая модель объекта строится в виде интеграла Дюамеля. Если на вход объекта можно подать функцию Хевисайда u(t)=1(t) или функцию Дирака δ(t), то наблюдая реакцию объекта можно оценить переходную характеристику объекта h(t) и весовую w(t). Подобный случай ранее был рассмотрен [1, с. 48]. Если подача на вход функции Дирака или функции Хевисайда затруднена, то представляет существенный теоретический и практический интерес способ нахождения весовой функции объекта при подаче на его вход некоторых гладких функций. Рассмотрим далее данный способ более подробно.

При проведении вычислительного эксперимента контроль входных и выходных переменных осуществлялся через некоторые промежутки времени ∆t. Представим некоторое гладкое входное воздействие в дискретном виде: 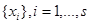, где s — объем выборки. Реакция объекта на входное воздействие имеет вид совокупности точек .

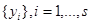Интеграл Дюамеля может быть представлен в дискретном виде:

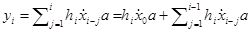
где a — величина шага в методе прямоугольников. Из данного уравнения можно выразить реализацию переходной характеристики :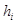

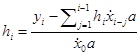
Далее восстановим весовую функцию на основе непараметрической оценки регрессии переходной характеристики:

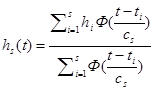
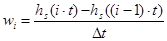
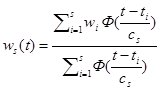
где 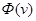- колоколообразная функция, 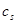- параметр размытости, 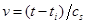, удовлетворяющие определенным условием сходимости [2, с. 286].

Вычисляя оценку регрессии описанным способом, мы попутно решаем задачу сглаживания переходной функции. Это облегчает дальнейшее взятие производной от переходной характеристики, вычисленной на основании зашумленных измерений входных x(t) и выходных y(t) переменных.

На последнем шаге, подставляя полученную оценку 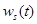 в интеграл Дюамеля, мы получим непараметрическую модель объекта и сможем прогнозировать его реакцию на измерения произвольных входных воздействий:

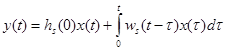
Приведем пример, иллюстрирующий результаты применения описанного алгоритма. Для этого рассмотрим линейный динамический объект второго порядка, который описывается уравнением следующего вида:

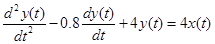
Пусть шаг дискретизации равен 0.02, помехи отсутствуют.

Подадим на вход объекта некоторое гладкое воздействие следующего вида:

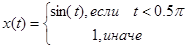
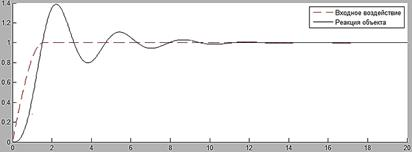
Рис. 1. Реакция объекта на гладкое входное воздействие

 

На рисунке ниже представлены результаты вычисления весовой характеристики. Для определения ее качества она сравнивается с истинной, аналитически вычисленной, весовой функцией. В результате можно увидеть, что данные функции практически совпадают (рисунок 2).

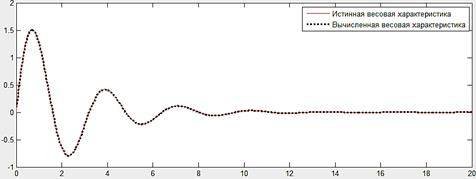
Рис. 2. Результаты вычисления весовой функции объекта

 

Построим непараметрическую модель объекта. Для оценки качества моделирования сравним выход объекта с выходом модели при одинаковых входных сигналах (рисунок 3).

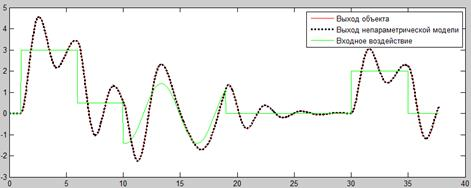
Рис. 3. Сравнение выхода модели и выхода объекта

 

Таким образом, используя описанный алгоритм идентификации, мы получаем качественную модель, довольно точно описывающую поведение объекта.

Построение непараметрического регулятора.

Весовую характеристику в составе интеграла Дюамеля можно рассматривать как линейный оператор A, взаимооднозначно отображающий пространство входных сигналов U в пространство выходных Y. Следовательно, можно найти такой обратный оператор 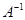, отображающий Y в U, где под Y мы будем понимать ту траекторию, которую мы хотим получить на выходе объекта, а под U — необходимое для этого управляющее воздействие. Сделать это можно подав на выход модели функцию Хевисайда, и сняв с входа значения обратной переходной характеристики, которая в составе интеграла Дюамеля представляет собой  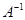[3, с. 6].

Рис. 4. Схема "включения" обратного оператора в систему

 

,

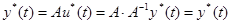где 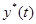- желаемая траектория, 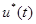– управляющее воздействие, обеспечивающее равенство выходной переменной объекта желаемому значению. Таким образом, мы получаем управление, приводящее систему в состояние, близкое к желаемому настолько, насколько точно удалось восстановить обратную весовую характеристику.

Опишем вычислительный алгоритм, используемый для построения непараметрического регулятора и отыскания необходимого управляющего воздействия 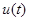. Для этого обратимся к следующему интегралу:

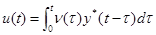
где 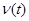 — обратная весовая характеристика, а  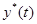— желаемая траектория. Обозначим через  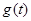обратную переходную функцию. Для ее нахождения в интеграле Дюамеля на место выходной переменной системы подставим функцию Хевисайда:

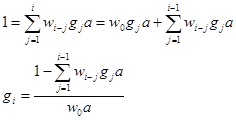
Для того чтобы получить обратную весовую характеристику, численно возьмем производную от обратной переходной характеристики, подставим 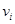  в численный аналог ранее упомянутого интеграла, и, произведя непараметрическое сглаживание, получим необходимое управляющее воздействие:

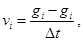
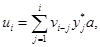
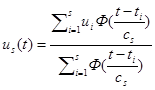
Таким образом, мы получили непараметрическую оценку управления 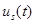, которое должно привести систему в состояние близкое к желаемому. Однако при построении регулятора необходимо обратить внимание на тот факт, что равенства желаемой траектории и выхода реального объекта достичь практически невозможно. Это объясняется наличием различных помех в системе, неточностью восстановления обратного оператора и т. д. Поэтому целесообразно ввести обратную связь, которая на основании сравнения действительной выходной величины и желаемого ее значения вносит коррективы в управляющее воздействие.

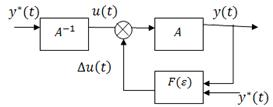
Рис. 5. Непараметрический регулятор с обратной связью

 

На данном рисунке 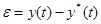- сигнал невязки,  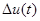— корректирующая добавка к управляющему воздействию.

Пусть желаемая траектория имеет следующий вид:

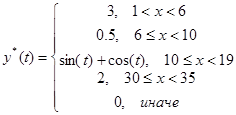
Найдем обратную весовую характеристику и необходимое управляющее воздействие (рис. 6, 7) для уже упомянутого ранее объекта.

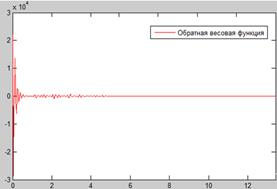
Рис. 6. Обратная весовая характеристика

 

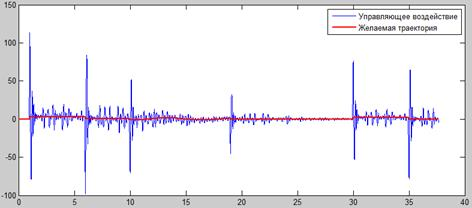
Рис. 7. Управляющее воздействие

 

На следующем рисунке приведены результаты управления первым объектом.

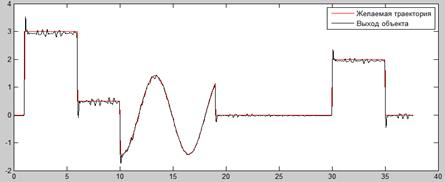
Рис. 8. Результаты управления объектом при помощи непараметрического регулятора

 

ПИД-регуляторы являются довольно распространённым и хорошо изученным типом регуляторов. Процесс настройки регулятора может производиться вручную или автоматически. Он, как правило, включает такие этапы, как: идентификация модели объекта, поиск области устойчивости коэффициентов, расчет параметров регулятора и их корректировка согласно какому-либо критерию качества. Однако в рассматриваемом случае, в условиях недостатка информации для построения параметрической модели, невозможно аналитически определить область устойчивости и начальное приближение. В данной работе настройка коэффициентов регулятора производится при помощи полученной непараметрической модели. Схема настройки представлена ниже.

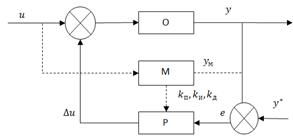
Рис. 9. Схема регулятора с настройкой коэффициентов при помощи модели

 

На данной схеме Р — это П-, ПИ- или ПИД-регулятор, М — модель объекта. Приведем описание одного из наиболее простых возможных алгоритмов расчета коэффициентов регулятора:

1.                  Задается начальное приближение коэффициентов 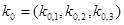 максимальное число итераций n.

2.                  Поочередно производится варьирование значений каждого из коэффициентов на некоторую величину 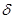. Вычисляется ошибка управления моделью объекта при текущих пробных значениях критерия 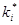, где i — текущая итерация. В случае если качество управления улучшилось, значение коэффициентов фиксируется .

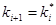3.                  Алгоритм продолжает свою работу пока номер итерации меньше заданного максимального количества итераций n.

Пусть исследователь находится в тех же условиях что и при построении непараметрического регулятора ранее. Построим для этого же объекта систему управления при помощи ПИД-регулятора, коэффициенты которого настраиваются по полученной ранее непараметрической модели.

Зададим n=100, , где 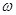 — некоторая равномерно распределенная случайная величина в пределах [0,1]. В качестве начального приближения был выбран нулевой вектор 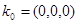, желаемая выходная траектория имеет такой же вид, как и при рассмотрении непараметрического регулятора. Итоговое значение вектора коэффициентов 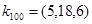. На рисунке ниже представлены линии выходных траекторий непараметрической модели объекта, полученные в процессе итерационного процесса настройки значений коэффициентов, а так же результаты управления самим объектом. На основании данных результатов можно заключить, что в данном случае регулятор успешно справляется с поставленной задачей управления.

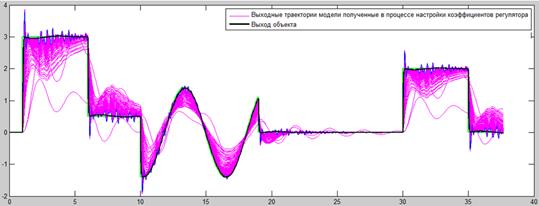
Рис. 10. Иллюстрация итерационного процесса настройки ПИД-регулятора и результатов его работы

 

Заключение.

В заключение хочется отметить, что рассмотрение алгоритмов, применимых в условиях непараметрической неопределенности является довольно сложной и актуальной на сегодняшний день задачей, заслуживающей особого внимания. Было рассмотрено два типа регулятора, которые могут быть использованы для построения систем управления в данном случае. В ходе вычислительных экспериментов, часть из которых представлена в данной статье, была подтверждена работоспособность рассматриваемых алгоритмов. В том числе были проведены успешные вычислительные эксперименты в случае, когда системы описываются дифференциальными уравнениями более высокого порядка, при различных значениях шага дискретизации и при наличии в каналах измерения переменных некоторой помехи.

 

Литература:

 

1.                  Medvedev A. V. Identification and control for linear dynamic systems of unknown order. // Optimization Techniques IFIP Technical Conference / Berlin — Heidelderg — New-York: Springer — Verlag, 1975. — СC. 48–55.

2.                  Надарая Э. А. Непараметрические оценки плотности вероятности и кривой регрессии. Тбилиси.: Тбил. ун-та. 1983, — 286 c.

3.                  Медведев А. В. О теории непараметрических систем управления/ А. В. Медведев. // Вестник Томского государственного университета, вып. 1 (22), Томск, 2013.- Стр. 6–19.