Усадочные процессы в наполненных полимерных композитах

Кинетические процессы усадки весьма информативны в исследовании природы процесса формирования полимерных композитов. Снижение усадочных деформаций обеспечивается введением в композитную систему наполнителей или заполнителей, что увеличивает структурную жёсткость.

Ключевые слова: структура, композит, усадка, внутренние напряжения.

При формировании изделий из полимерных композитных материалов (ПКМ), проявляются усадочные процессы, которые оказывают непосредственное влияние как на внешний вид и форму изделий, так и на физико-механические показатели композитов [1–3]. Как правило, усадка обусловлена миграцией и испарением растворителя, в результате возникают внутренние напряжения, которые в последующем могут привести к растрескиванию материала [1, 2]. В целом, усадочные процессы оказывают негативное влияние на качественные показатели изделий и поэтому их изучению необходимо уделять особое внимание.

Усадка является самопроизвольным процессом, развивающимся в течение времени. В этой связи кинетика усадки весьма информативна в исследовании природы процесса формирования ПКМ. Испарение растворителя приводит к появлению свободного объёма, что сопровождается уменьшением линейных размеров, повышением уровня внутренних напряжений, растрескиванием и связанным с этим искажением исходной формы изделий. Модель линейной усадки представлена на рис. 1.

Усадочные процессы непосредственно связаны с состоянием жёсткого структурного каркаса композита. Снижение усадочных деформаций обеспечивается введением в композитную систему наполнителей или заполнителей, что увеличивает количество связей в структурном каркасе и повышает его жёсткость [1, 2]. Кроме того, в наполненных композитах происходит трансформирование матричного материала в плёночное состояние. Известно, что плёночная матрица менее подвержена усадке, поскольку в ней отсутствует естественный признак усадки — признак массивности матрицы. В начальный период скорость усадки максимальна. При этом максимален и объём композита, не затронутый усадочными процессами. В дальнейшем, локальные усадочные объёмы разрастаются, взаимодействия между собой и в результате захватывают весь объём композита. Таким образом, скорость усадки падает до нуля, а абсолютная величина линейной усадки стабилизируется на своём асимптотическом значении .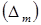

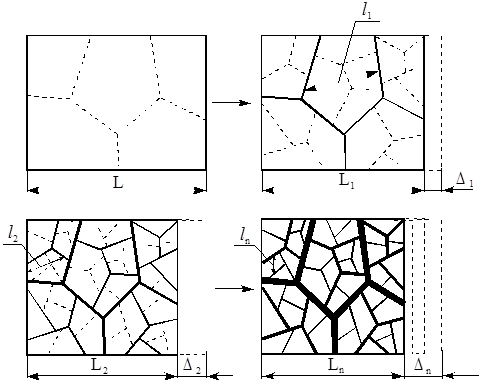
Рис. 1. Модель линейной усадки композита, где 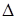 — линейная усадка.

В подобной интерпретации просматривается явная аналогия кинетики усадки с процессом кинетики роста прочности (модуля упругости) композита при твердении. В общем случае, для кинетических процессов скорость изменения контролируемого параметра 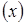 пропорциональна величине самого параметра

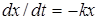,                                                                                                             (1)

где 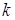 — постоянная величина.

Здесь знак минус указывает на то, что с течением времени параметр 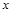 уменьшается до стационарного значения. Такое поведение характеризует самозатухающие процессы, которые часто наблюдаются в кинетических закономерностях композитов [1, 2, 4–7].

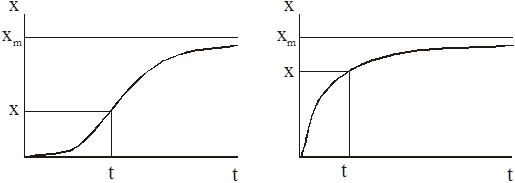
Графически кинетика формирования физико-механических характеристик изображается в виде кривых, представленных на рис. 2.

Общим для этих закономерностей является то обстоятельство, что они имеют асимптотический предел 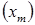, к которому с течением времени стремится величина 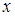. Тем не менее, приведенные зависимости имеют существенные отличия и описывают различные процессы.

Произведем модельный анализ процесса кинетики с асимптотическим приближением. Для этого воспользуемся методом возмущений, который заключается в следующем. Если стабилизированный параметр 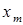 изменить на величину 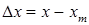, за счет внешнего возмущающего воздействия, а затем снять это возмущение, то параметр  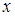с течением времени вновь вернется к своему асимптотическому пределу, соответствующему кинетически стабилизированному значению .

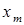                                        а)                                                                    б)

Рис. 2. Типичные закономерности изменения физико-механических характеристик [1, 6].

В соответствии с этой моделью уравнение (1) запишется в виде

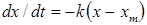.                                                                                                 (2)

В исходных равенствах (1) и (2) не учтено весьма важный момент, что скорость изменения параметра 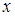 пропорциональна не только величине самого параметра, но и характерному структурному размеру ПКМ.

Тогда начальное равенство (1) будет иметь следующий вид

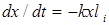,                                                                                                           (3)

где l_i _ относительный структурный размер системы, являющийся геометрическим показателем, выраженным через размерность композитной системы и зависящий от аргументного параметра.

При l_i =1 выражение (3) принимает классическую форму (1). Следовательно, в качестве размера l_i могут выступать показатели линейных поверхностных или объемных структур, либо аналогичные показатели фрактальных образований.

Поскольку композитные гетерогенные системы имеют несколько фаз, следовательно, размер каждой из них должен учитываться. Для выяснения этого перепишем кинетическую зависимость с асимптотическим приближением (2), с учетом условия (3), в виде

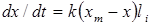.                                                                                                (4)

Представленная форма равенства позволяет дать характеристику структурному размеру l_i. Из (4) следует, что в данном выражении должен учитываться тот структурный размер, рост которого приводит к увеличению скорости изменения изучаемого параметра .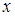

В нашем случае для процесса усадки характерным структурным размером, отвечающим условию (4), является размер объёма композита, не затронутого усадочными деформациями, и пропорциональному скорости усадки.

В этой связи зависимость (4) принимает вид

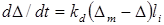.                                                                                             (5)

В процессе усадки наблюдается сопутствующее трещинообразование [1, 8–10]. В результате образуется иерархическая сеть трещин с выраженной автомодельностью. Трещины, возникающие в начальный период, имеют наибольшее раскрытие и образуют сеть с наибольшими ячейками 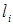. В дальнейшем формируются более мелкие трещины с меньшим раскрытием (см. рис. 1). Итоговая топология проявляется в виде фрактальной структуры трещиноватости.

В соответствии с равенством (5), кинетика усадки описывается зависимостью

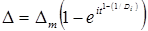,                                                                                                 (6)

где 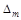_ максимальная усадка,  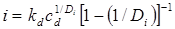_ постоянная величина.

Кинетика усадки проверялась по экспериментальным данным для полиэфирного, фурфуролацетонового и эпоксидного композитов (рис. 3). Показатель 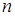, характеризующий размерность структуры, оказывающей преимущественное влияние на процессы усадки, определялся по результатам линейного регрессионного анализа, из уравнения 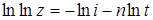, где 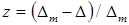_ новая переменная.

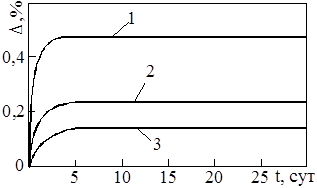
Рис. 3. Кинетические усадочные процессы в полимерных композитах: 1 — полиэфирного (смола ПН-1, наполненная керамзитом); 2 — фурфуролацетонового, наполненный молотым кварцевым песком; 3 — эпоксидного (диановая смола ЭД-20, наполненная молотым гранитом)

Таким образом, линейный регрессионный анализ показал, что для всех исследованных ПКМ показатель 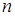 изменялся в интервале 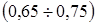. Соответствующая найденному показателю внешняя (хаусдорфова) размерность, ответственной за усадку структуры в среднем составляет  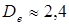и отвечает фрактальной размерности полидисперсного структурного каркаса из частиц наполнителя и плёночной фазы матрицы.

Литература:

1.                  Бобрышев, А. Н. Структура и свойства дисперсно-наполненных композитных материалов / А. Н. Бобрышев, А. В. Лахно, Р. В. Козомазов, А. А. Бобрышев. — Пенза: Изд-во ПГУАС, 2012. — 160 с.

2.                  Козомазов, В. Н. Структура и свойства высоконаполненных строительных полимерных композитов: автореф. дис.... докт. техн. наук / В. Н. Козомазов — Москва, 1996. — 45 с.

3.                  Семов, И. Н. Ремонт корпусных деталей машин /И. Н. Семов, Ю. А. Захаров, Е. Г. Рылякин // Новый университет. Серия «Технические науки». — № 10(32). — 2014. — С.53–55. [ISSN 2221–9552]

4.                  Новиков, Е. В. Кинетические процессы в композитах при воздействии агрессивных сред / Е. В. Новиков, П. В. Воронов, А. В. Лахно, А. Н. Бобрышев // Международный технико-экономический журнал. 2014. № 6. С. 95–102.

5.                  Будылина Е. А. Математическое моделирование кинетических процессов в дисперсных системах / Е. А. Будылина, И. А. Гарькина, Я. И. Сухов // Молодой ученый. — 2013. — № 12. — С. 104–107.

6.                  Лахно, А. В. Кинетические процессы в композитных системах / А. В. Лахно, П. В. Воронов, А. Н. Бобрышев // Germany: LAP Lambert Academic Publishing GmbH & Co. KG. — 2011. — 116 с.

7.                  Воронов, П.В. Оценка кинетики фазовых переходов в твердеющих гетерогенных материалах / П. В. Воронов, А. Н. Бобрышев, А. В. Лахно, П. И. Кувшинов, Н. Н. Туманова // Региональная архитектура и строительство. 2010. № 2. С. 58–66.

8.                  Лахно, А.В. Некоторые аспекты усиления полимерных композитов / А. В. Лахно, А. Н. Бобрышев, П. А. Зубарев, В. О. Петренко, Е. В. Новиков // Международный технико-экономический журнал. 2012. № 5. С. 100–105.

9.                  Бобрышев, А.Н., Анализ распределения наполнителя в структуре композитов // А. Н. Бобрышев, П. А. Зубарев, П. И. Кувшинов, А. В. Лахно // Интернет-Вестник ВолгГАСУ. 2012. № 1 (20). С. 28.

10.              Новиков, Е.В. Кластеро- и трещинообразование в композитах / Е. В. Новиков, А. В. Лахно, А. Н. Бобрышев, П. А. Зубарев // Международный технико-экономический журнал. 2012. № 5. С. 96–99.