Целью статьи является разработка программного продукта, который выполняет демонстрацию явления преломления лучей на границе раздела двух сред. Необходимо разработать программный продукт с удобным интерфейсом, позволяющий выполнить демонстрацию преломления луча в зависимости от угла падения и свойств сред.
Программный продукт должен правильно работать при любых корректно заданных исходных данных. В случае неправильного ввода исходных данных должно быть предложено повторить ввод. Исходные данные должны вводиться как с клавиатуры, так и из файла.
При выполнении операции расчета угла преломления входными данными являются показатели преломления сред и угол падения. Входные данные поступают либо с клавиатуры, либо из файла.
Выходными данными является угол преломления луча. Выходные данные выводятся на экран монитора и в файл.
Рассмотрим падение плоской волны на границу, разделяющую две прозрачные однородные диэлектрические среды с показателями преломления 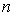 и
и 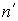 . Будем считать, что граница представляет собой плоскость (так как в пределах бесконечно малой области любую поверхность можно считать плоской). Будем также считать, что сама граница раздела свет не поглощает.
. Будем считать, что граница представляет собой плоскость (так как в пределах бесконечно малой области любую поверхность можно считать плоской). Будем также считать, что сама граница раздела свет не поглощает.
После прохождения границы раздела двух сред падающая плоская волна (луч 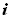 ) разделяется на две волны: проходящую во вторую среду (луч
) разделяется на две волны: проходящую во вторую среду (луч 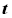 ) и отраженную (луч
) и отраженную (луч 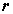 ) (рис.1)
) (рис.1)
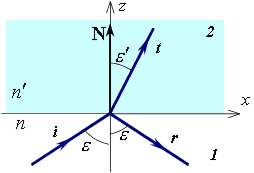
Рис. 1. Преломление и отражение света на границе двух сред.
На рис.1. N — вектор нормали к поверхности в точке падения единичной длины 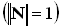 . Поместим начало координат в точку падения. Определим следующие величины:
. Поместим начало координат в точку падения. Определим следующие величины:
Угол падения 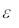 – это угол между лучом
– это угол между лучом 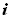 , падающим на преломляющую или отражающую поверхность, и нормалью
, падающим на преломляющую или отражающую поверхность, и нормалью 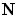 к поверхности в точке падения.
к поверхности в точке падения.
Угол преломления 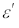 – это угол между преломленным лучом
– это угол между преломленным лучом 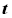 и нормалью
и нормалью 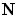 к поверхности в точке преломления.
к поверхности в точке преломления.
Угол отражения 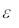 – это угол между отраженным лучом
– это угол между отраженным лучом 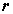 и нормалью
и нормалью 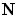 к поверхности в точке отражения.
к поверхности в точке отражения.
Закон преломления
После прохождения светом границы раздела двух сред необходимо определить направление распространения преломленной волны 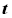 и отраженной волны
и отраженной волны 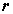 , и распределение энергии между отраженной и преломленной волной.
, и распределение энергии между отраженной и преломленной волной.
В соответствии с уравнением плоской волны запишем выражения для комплексных амплитуд падающей, отраженной и преломленной волн:
уравнение падающей плоской волны
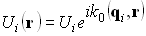
уравнение преломленной плоской волны
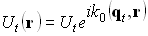
уравнение отраженной плоской волны
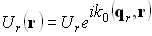 где
где 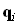 ,
, 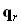 ,
, 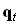 – оптические векторы падающей, отраженной и преломленной волн,
– оптические векторы падающей, отраженной и преломленной волн, 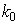 – волновое число,
– волновое число, 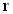 – радиус-вектор произвольной точки.
– радиус-вектор произвольной точки.
Здесь мы используем соотношения скалярной теории, поскольку закон преломления одинаков для векторных и скалярных волн.
Из уравнений падающей и преломленной плоской волны следует, что на границе раздела двух сред у падающей и преломленной волн амплитуды могут быть различны, но должны совпадать значения эйконалов (этого требует условие физической реализуемости, так как иначе волна будет иметь разрыв на границе раздела):
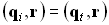
Это равенство соблюдается на границе раздела, то есть для всех 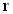 , перпендикулярных вектору нормали. Таким образом, выражение можно записать в виде:
, перпендикулярных вектору нормали. Таким образом, выражение можно записать в виде:
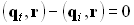 при
при 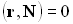 или:
или: 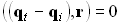 при
при 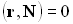
То есть 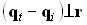 , если
, если 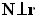 . Выполнение этих условий возможно тогда и только тогда, когда
. Выполнение этих условий возможно тогда и только тогда, когда 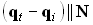 . Таким образом, можно вывести формулировки закона преломления в векторной форме:
. Таким образом, можно вывести формулировки закона преломления в векторной форме:
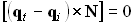 или:
или:
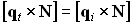
Так как длина оптического вектора равна показателю преломления среды (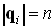 ,
, 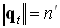 ), то из выражения и определения векторного произведения можно вывести классический закон преломления Снеллиуса.
), то из выражения и определения векторного произведения можно вывести классический закон преломления Снеллиуса.
Качественная часть закона:
Падающий луч, преломленный луч и нормаль к поверхности раздела двух сред в точке падения лежат в одной плоскости.
Количественная часть закона:
Произведение показателя преломления на синус угла между лучом и нормалью сохраняет свое значение при переходе в следующую среду:
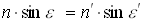
Чтобы найти скаляр 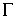 , домножим скалярно выражение на вектор нормали
, домножим скалярно выражение на вектор нормали 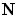 :
:
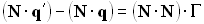
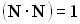 ,
,
следовательно
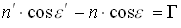
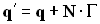 ,
,
где
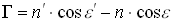
Величина 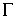 имеет большое значение в математическом аппарате расчета лучей на компьютере.
имеет большое значение в математическом аппарате расчета лучей на компьютере.
В основной программе выполняется единственная процедура MainCycle.
Перед основным циклом на экран выводятся реквизиты пользователя из файла "recv. txt". Затем выполняется установка входных данных по умолчанию, запись этих данных в файл, прорисовка графика и меню. Вызов меню выполняется в бесконечном цикле до тех пор, пока пользователь не выберет пункт "Выход". При выборе пункта "Информация" на экран будет выведена основная информация о преломлении света (процедура Info). При выборе пункта "Считать данные из файла" программа загрузит данные из файла "data. txt". При выборе пунктов "Изменить показатель преломления в 1-й среде", "Изменить показатель преломления во 2-й среде", "Изменить угол падения" можно менять соответствующие входные данные. При любом изменении данных результаты автоматически отображаются на графике и сохраняются в файл.
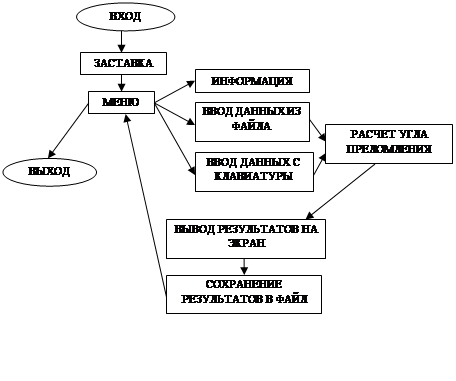
Рис. 2. Схема функционирования программы
Я использовал в своей работе модули Graph и Crt (для работы с графическим и текстовым режимом соответственно).
Модуль Crt реализует работу в текстовом режиме. С помощью его процедур и функций можно проверять содержимое буфера клавиатуры и проверять код введенного символа.
Graph позволяет работать с графическим режимом. С его помощью возможно отображение графических объектов. При помощи модуля Graph я выполнил прорисовку меню и графика.
В результате выполнения работы я создал программный продукт, имитирующий модель преломления лучей на границе двух сред. Требования, изложенные в техническом задании, выполнены.
Я разработал удобный интерфейс, функцию вывода графика, отображающего преломление лучей на границе двух сред. Также имеется возможность работы с разными преломляющими средами, и смены угла падения.
Литература:
1. Фаронов В.В. "Турбо Паскаль 7.0. Начальный курс. " Учебное издание — М.: Нолидж, 2000, 575 с.
2. Н. Культин "Turbo Pascal в задачах и примерах" — С.: БХВ-Петербург, 2004,256 с.
3. Ахманов С. Г "Физическая оптика. Учебник (Ахманов)" — С.: МГУ, 2004, 213 с.
4. Федоров А. "Особенности программирования на Borland Pascal" — Киев: Диалектика, 1994, 144 с.







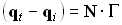 где
где 