Основная цель работы — показать, как решаются основные задачи исследования операций, такие как задача линейного программирования, транспортная задача, задача о назначении, задача о коммивояжере, матричная игра в MathCAD.
Ключевые слова: исследование операций, задача линейного программирования, транспортная задача, задача о назначении, задача о коммивояжере, матричная игра, решения задач в MathCAD.
1. Управление и планирование являются наиболее сложными функциями в работе предприятий, фирм, служб администраций всех уровней. Долгое время они являлись монополией человека с соответствующей подготовкой и опытом работы [1–3].
Создание компьютеров и программных средств создало огромные возможности для развития науки, совершенствования методов планирования и управления производством. Однако без строгих формулировок задач, без математического описания процессов современный уровень управления и планирования не может быть достигнут. В последнее время появились математические системы- математические программы, позволяющие решить многие задачи без составления компьютерных программ, такие как MathCAD, Maple, Mathematica и т. д. [3–5].
Задачи управления и планирования обычно сводятся к выбору некоторой системы параметров и функций, которые приводят к экстремальным задачам следующего вида.
Требуется найти максимум или минимум функции
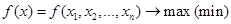 (1)
(1)
при условиях:
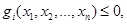 (2)
(2)
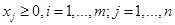 . (3)
. (3)
где 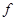 ,
, 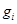 — функции,
— функции, 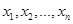 — параметры управления [1–3].
— параметры управления [1–3].
Выражение (1) называется функцией цели. Условия (2),(3) представляют собой ограничения поставленной задачи. Условия (3) справедливы для многих задач, особенно экономических, когда параметры управления 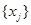 по своему физическому смыслу не могут быть отрицательными. Среди условий задачи могут быть равенства.
по своему физическому смыслу не могут быть отрицательными. Среди условий задачи могут быть равенства.
Математическая дисциплина, занимающаяся изучением экстремальных (максимальных или минимальных) задач управления, планирования и разработкой методов их решения, получила название исследования операций.
2. Решение задачи линейного программирования в MathCAD.
В задаче линейного программирования целевая функция и ограничения линейны:
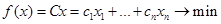 , (4)
, (4)
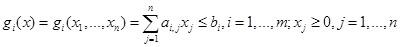 . (5)
. (5)
Здесь в неравенствах возможны знаки 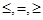 . Когда все ограничения заданы равенствами, то говорят о канонической задаче линейного программирования, в остальных случаях — об общей задаче линейного программирования. Вводя матрицу
. Когда все ограничения заданы равенствами, то говорят о канонической задаче линейного программирования, в остальных случаях — об общей задаче линейного программирования. Вводя матрицу 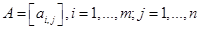 , и векторы
, и векторы 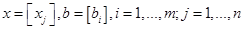 , ограничения можно задавать в векторно-матричном виде
, ограничения можно задавать в векторно-матричном виде 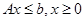 .
.
Каноническая задача линейного программирования решается с помощью хорошо известного симплекс метода [1–3]. Здесь мы покажем, как можно решить задачу линейного программирования с помощью математической системы MathCAD.
Решим задачу ([1],21.1). После знака // записываем замечание-смысл команд MathCAD.
ORIGIN: =1 m: =2 n: =4 i: =1..m j: =1..n // ввод конечных значений индексов
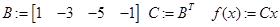 // целевая функция
// целевая функция
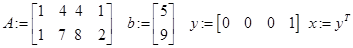 // матрица и вектор ограничений
// матрица и вектор ограничений
Given 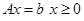
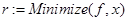 // обращение к внутренней функции
// обращение к внутренней функции
 // вывод результатов
// вывод результатов
Переменная 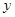 введена для экономии места. Здесь и дальше в блоке Given …Minimize знаки равенств и неравенств жирные. Они набираются в панели MathCAD булево.
введена для экономии места. Здесь и дальше в блоке Given …Minimize знаки равенств и неравенств жирные. Они набираются в панели MathCAD булево.
3. Решение транспортной задачи в MathCAD. Задачи о назначении и коммивояжере.
В организации перевозок некоторого продукта (груза) между пунктами его производства 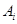 ,
, 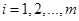 , и пунктами потребления
, и пунктами потребления 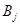 ,
, 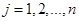 , возникает транспортная задача. Каждый пункт производства
, возникает транспортная задача. Каждый пункт производства 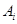 характеризуется запасом продукта
характеризуется запасом продукта 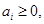
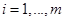 . Каждый пункт потребления
. Каждый пункт потребления 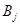 характеризуется потребностью в продукте
характеризуется потребностью в продукте 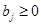 ,
, 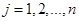 . Сеть дорог, соединяющая систему рассматриваемых пунктов, моделируется с помощью матрицы
. Сеть дорог, соединяющая систему рассматриваемых пунктов, моделируется с помощью матрицы 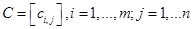 . Элемент
. Элемент 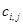 представляет собой нормы затрат на перевозку единицы груза из пункта производства
представляет собой нормы затрат на перевозку единицы груза из пункта производства 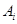 в пункт потребления
в пункт потребления 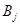 . Через
. Через 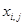 обозначим количество продукта, перевозимого из пункта
обозначим количество продукта, перевозимого из пункта 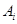 в пункт
в пункт 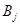 . Тогда план перевозок груза представляется в виде матрицы:
. Тогда план перевозок груза представляется в виде матрицы:
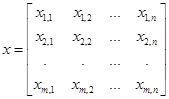 .
.
Транспортная задача ставиться так:
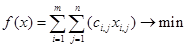 , (6)
, (6)
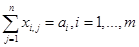 , (7)
, (7)
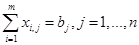 . (8)
. (8)
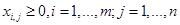 . (9)
. (9)
Для решения закрытой транспортной задачи, т. е. для случая 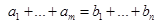 , хорошо известным методом является метод потенциалов [1–3].
, хорошо известным методом является метод потенциалов [1–3].
С транспортной задачей связаны задачи о назначении и о коммивояжере.
Задача о назначении формулируется таким образом: для реализации производственного процесса необходимо выполнить 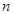 операций. Имеется
операций. Имеется 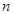 рабочих, которые способны осуществить их, и время (затраты) выполнения каждым рабочим любой из
рабочих, которые способны осуществить их, и время (затраты) выполнения каждым рабочим любой из 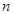 операций. Требуется определить: кто и какую операцию должен выполнить, чтобы суммарное время (затраты) выполнения всего производственного процесса было минимально. Возможны и другие постановки.
операций. Требуется определить: кто и какую операцию должен выполнить, чтобы суммарное время (затраты) выполнения всего производственного процесса было минимально. Возможны и другие постановки.
Формализация задачи. Введём матрицу, 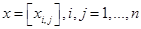 , где
, где 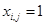 при
при 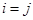 и
и 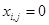 при
при 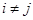 . Тогда каждый рабочий может выполнить лишь одну операцию и справедливо ограничение:
. Тогда каждый рабочий может выполнить лишь одну операцию и справедливо ограничение:
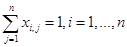 . (10)
. (10)
Каждая операция может выполняться лишь одним рабочим и справедливо ограничение:
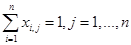 . (11)
. (11)
Матрица системы (10,11) имеет ранг 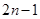 , т. е. из
, т. е. из 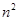 неизвестных
неизвестных 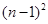 являются свободными.
являются свободными.
Если обозначить себестоимость выполнения 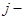 операции
операции 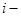 рабочим через
рабочим через 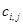 , то суммарная себестоимость выполнения всех работ будет:
, то суммарная себестоимость выполнения всех работ будет:
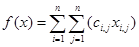 . (12)
. (12)
Задача о назначении заключается в минимизации сумму (12) при выполнении ограничений (10), (11) и 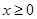 . Для решения задачи о назначении разработан венгерский метод [1–3]. В решении задачи в матрице
. Для решения задачи о назначении разработан венгерский метод [1–3]. В решении задачи в матрице 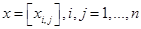 , в главной диагонали могут стоять либо 1 либо 0, но в каждой строке и столбце могуть стоять только по одной 1. Матрица С есть матрица себестоимости выполнения соответствующих операций.
, в главной диагонали могут стоять либо 1 либо 0, но в каждой строке и столбце могуть стоять только по одной 1. Матрица С есть матрица себестоимости выполнения соответствующих операций.
Задача о коммивояжере формулируется таким образом: имеется 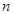 городов, выезжая из исходного города
городов, выезжая из исходного города 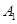 , коммивояжер должен побывать в каждом городе
, коммивояжер должен побывать в каждом городе 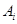 по одному разу и должен вернуться в город
по одному разу и должен вернуться в город 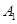 . Задача заключается в определении последовательности городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т. д.
. Задача заключается в определении последовательности городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т. д.
Задача о коммивояжере формализуется как задача о назначении, но только в матрице решений 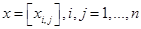 , в главной диагонали всегда должна стоять 0. Кроме того, в матрице С в главной диогонали должны стоять большие числа.
, в главной диагонали всегда должна стоять 0. Кроме того, в матрице С в главной диогонали должны стоять большие числа.
Здесь мы покажем, как можно решить транспортную задачу, задачи о назначении и о коммивояжере с помощью математической системы MathCAD. Ясно, что задачи о назначении и о коммивояжере являются частными случаями транспортной задачи.
Решим сначала транспортную задачу ([1],23.1).
ORIGIN: =1 m:=3 n: =4 i: =1..m j: =1..n // ввод конечных значений индексов
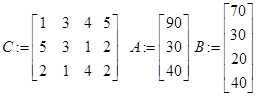
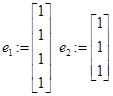 // матрица и вектор ограничений
// матрица и вектор ограничений
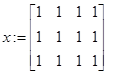 //начальный план перевозок
//начальный план перевозок
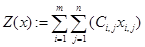 // целевая функция
// целевая функция
Given 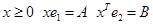 // обращение к внутренней функции
// обращение к внутренней функции
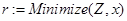
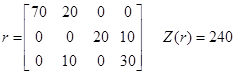 // вывод результатов
// вывод результатов
Решим теперь задачу о назначении ([1], 26.1).
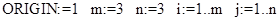 //индексы
//индексы
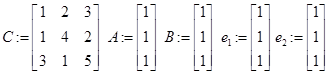 //матрица и вектор ограничений
//матрица и вектор ограничений
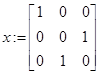 // начальное приближение
// начальное приближение
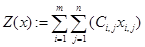 // целевая функция
// целевая функция
Given 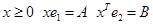 // внутренняя функция
// внутренняя функция
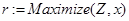
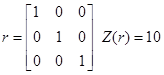 // вывод результатов
// вывод результатов
Given 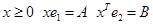 // внутренняя функция
// внутренняя функция
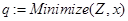
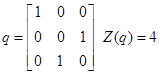 // вывод результатов
// вывод результатов
Решим теперь задача о коммивояжере [5].
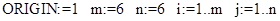 // индексы
// индексы
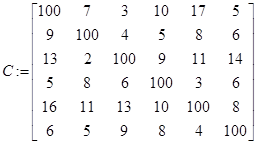
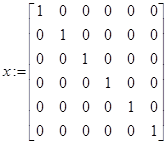 // платёжная матрица
// платёжная матрица
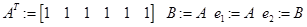 // векторы ограничений
// векторы ограничений
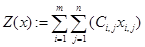
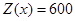 // целевая функция
// целевая функция
Given
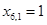
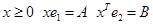
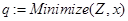 // внутренняя функция
// внутренняя функция
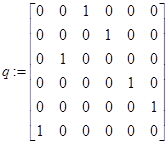
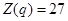 // вывод результатов
// вывод результатов
4. Решение матричных игр в MathCAD.
Матричные игры задаются платёжной матрицей 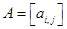 ,
, 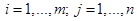 .
.
В матричной игре участвуют два игрока. Строки являются чистыми стратегиями первого игрока, а столбцы являются чистыми стратегиями второго игрока. Гарантированный выигрыш первого игрока, применяющего 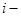 ю стратегию равен
ю стратегию равен 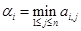 . Число
. Число
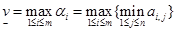
называется нижним значением игры, и называется максиминной стратегией первого игрока. Аналогично, число
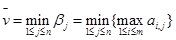
называется верхним значением игры. Всегда 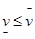 . Если
. Если 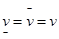 , то игра имеет седловую точку в чистых стратегиях, а число
, то игра имеет седловую точку в чистых стратегиях, а число 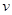 называется значением (ценой) игры. Если игра имеет седловую точку, то существует элемент матрицы
называется значением (ценой) игры. Если игра имеет седловую точку, то существует элемент матрицы 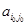 такой, что
такой, что
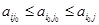 . (13)
. (13)
Если игра не имеет седловую точку в чистых стратегиях, то по теореме Фона Неймана, игра имеет седловую точку в смешанных стратегиях. Для этого определяем вероятности
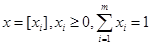 ,
, 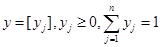 . (14)
. (14)
Смысл этих вероятностей заключаются в следующем. Первый игрок выбирает свою 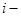 ю чистую стратегию с вероятностью
ю чистую стратегию с вероятностью 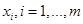 , а второй игрок выбирает свою
, а второй игрок выбирает свою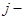 ю чистую стратегию с вероятностью
ю чистую стратегию с вероятностью 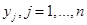 . Если первый игрок выбирает свою
. Если первый игрок выбирает свою 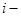 ю чистую стратегию с вероятностью
ю чистую стратегию с вероятностью 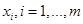 , а второй игрок выбирает свою
, а второй игрок выбирает свою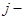 ю чистую стратегию с вероятностью
ю чистую стратегию с вероятностью 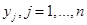 , то средний выигрыш первого игрока равен
, то средний выигрыш первого игрока равен
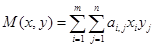 . (15)
. (15)
Выигрыш 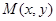 называется функцией игры. Пара смешанных стратегий
называется функцией игры. Пара смешанных стратегий 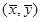 называется седловой точкой функции
называется седловой точкой функции 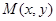 , если
, если
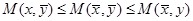 . (16)
. (16)
Задача максимизации гарантированного выигрыша первого игрока и задача минимизации гарантированного проигрыша второго игрока сводятся к паре двойственных задач линейного программирования:
Задача первого игрока заключается в следующем
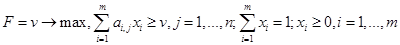 . (17)
. (17)
Задача второго игрока заключается в следующем
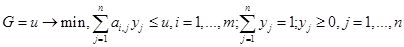 . (18)
. (18)
Процесс решения задач упрощается, если перейти к переменным
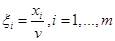 ;
; 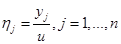 .
.
Это возможно, если 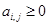 . Если так, то имеем:
. Если так, то имеем:
Задача первого игрока принимает вид
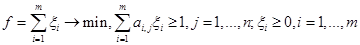 . (19)
. (19)
Задача второго игрока принимает вид
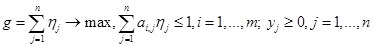 . (20)
. (20)
Оптимальные стратегии игроков не изменится, если матрицу игры 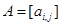 заменить матрицей
заменить матрицей 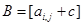 . Так как, при этом цена игры увеличивается на
. Так как, при этом цена игры увеличивается на 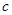 .
.
Решим задачу ([1],31.3)
ORIGIN: =1 // начальное значение индексов
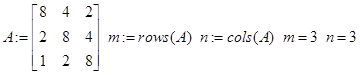 // платёжная матрица
// платёжная матрица
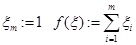 // целевая функция
// целевая функция
Given 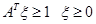 // внутренняя функция
// внутренняя функция
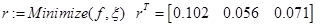
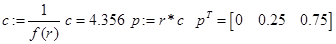 // вывод результатов
// вывод результатов
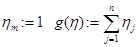 // целевая функция
// целевая функция
Given 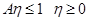 // внутренняя функция
// внутренняя функция
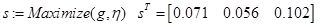 // внутренняя функция
// внутренняя функция
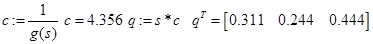 // вывод результатов
// вывод результатов
Литература:
1. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании: Учеб. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.
2. Таха Х. А. Введение в исследование операций, 7-е издание.: Пер. с англ. — М.: Издательский дом «Вильямс», 2005. — 912 с: ил. — Парал. тит. англ.
3. Охорзин В. А. Прикладная математика в системе MathCAD. -СПб, Лань.2008.-352 с.
4. Имомов А «Организация приближённого решения интегральных уравнений в MathCAD». Молодой учёный, № 14(73), сентябрь 1, 2014 г.-с.6–15.
5. Мусатенко К. Е., Раводин О. М. Компьютерная модель для лабораторной работы «Выбор оптимальной траектории движения транспортного робота с использованием задачи о коммивояжере». Молодой учёный, 12 (59), 2013 г.-с.71–75.







