При оптимизации состава бетона на мелкозернистых песках весьма важно произвести объективную оценку их влияния на технологические свойства бетонной смеси. Известные способы учета влияния мелкозернистых заполнителей на консистенции бетонной смеси [1,2] лишь косвенно характеризуют свойства песка в бетоне. Предложенная методика оценки качества песков по величине их водопотребности (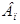 ) с учетом прямо пропорциональной зависимости между
) с учетом прямо пропорциональной зависимости между 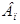 и водопотребностью бетонной смеси (
и водопотребностью бетонной смеси (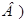 [1], как показали опытные данные (рис.1), справедлива только для стандартных заполнителей.
[1], как показали опытные данные (рис.1), справедлива только для стандартных заполнителей.
В связи с этим нами проведены исследования по изучению влияния качества различных песков на технологические свойства бетона и разработаны два способа оценки качества мелких заполнителей, позволяющие использовать их при проектировании составов бетонной смеси заданной консистенции. При этом качество песков оценивается комплексным структурным параметром  , которых входит в уравнение вибровязкости цементно-песчаного раствора, имеющее вид:
, которых входит в уравнение вибровязкости цементно-песчаного раствора, имеющее вид:
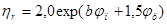 , (1)
, (1)
где 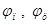 — параметры насыщения раствора песком и цементного теста вяжущим:
— параметры насыщения раствора песком и цементного теста вяжущим:
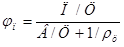 ; (2)
; (2)
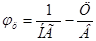 , (3)
, (3)
в этих выражениях 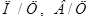 - песчано-цементное и водоцементное отношения;
- песчано-цементное и водоцементное отношения; 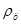 - плотность вяжущего;
- плотность вяжущего; 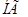 - нормальная густота цементного теста в относительных единицах.
- нормальная густота цементного теста в относительных единицах.
Параметр, характеризующий качество песка 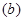 в уравнении (1) может быть определен либо по экспериментальным данным консистенции бетонной смеси (испытанием песка в бетоне), либо по водопотребности песка, устанавливаемой по методике, приведенной в работе [1].
в уравнении (1) может быть определен либо по экспериментальным данным консистенции бетонной смеси (испытанием песка в бетоне), либо по водопотребности песка, устанавливаемой по методике, приведенной в работе [1].
Для установления значения параметра 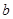 по первому способу достаточно произвести два замеса различным песчано-цементным отношениям при постоянном водоцементном факторе
по первому способу достаточно произвести два замеса различным песчано-цементным отношениям при постоянном водоцементном факторе 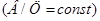 и определить соответствующие значения опытной консистенции (вязкости) бетонной смеси. В случае определения консистенции смеси по осадке стандартного конуса
и определить соответствующие значения опытной консистенции (вязкости) бетонной смеси. В случае определения консистенции смеси по осадке стандартного конуса 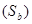 , переход к расчетной вязкости
, переход к расчетной вязкости 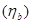 осуществляется по формуле (1), приведенной в работе [3]. В данном способе параметр
осуществляется по формуле (1), приведенной в работе [3]. В данном способе параметр 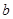 вычисляется по формуле:
вычисляется по формуле:
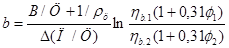 , (4)
, (4)
где 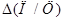 - разница песчано-цементных отношений двух замесов бетонной смеси;
- разница песчано-цементных отношений двух замесов бетонной смеси; 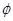 — параметр насыщения бетонной смеси крупным заполнителем, равный
— параметр насыщения бетонной смеси крупным заполнителем, равный
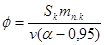 , (5)
, (5)
где 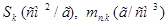 и
и 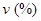 — удельная поверхность, насыпная масса и пустотность крупного заполнителя соответственно.
— удельная поверхность, насыпная масса и пустотность крупного заполнителя соответственно.
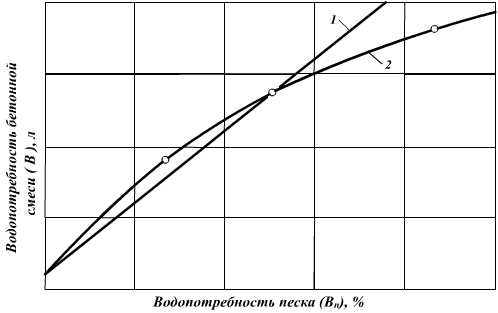
Рис. 1. График зависимости 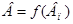 : 1 — по данным [1]; 2 — по опытным данным
: 1 — по данным [1]; 2 — по опытным данным
Насыпная масса и пустотность крупного заполнителя определяются стандартными способами, а удельная поверхность может быть вычислена (на основании гранулометрического анализа) по формуле:
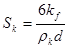 , (6)
, (6)
где 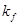 - коэффициент, характеризующий геометрическое очертание зерен заполнителя (коэффициент формы), определяемый на основании петрографического анализа;
- коэффициент, характеризующий геометрическое очертание зерен заполнителя (коэффициент формы), определяемый на основании петрографического анализа; 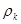 - плотность щебня (гравия);
- плотность щебня (гравия); 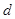 - средняя крупность (средний расчетный диаметр) зерен, которая определяется из выражения:
- средняя крупность (средний расчетный диаметр) зерен, которая определяется из выражения:
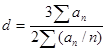 , (7)
, (7)
здесь 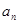 - частные остатки в % на стандартных ситах, начиная с сита наименьшего размера;
- частные остатки в % на стандартных ситах, начиная с сита наименьшего размера; 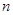 - размер отверстия соответствующего сита.
- размер отверстия соответствующего сита.
Значение коэффициента формы 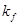 в формуле (6) оценивается отношением истинной поверхности одного зерна заполнителя к его расчетной, определенной по выбранной зависимости. Следовательно, можно выразить:
в формуле (6) оценивается отношением истинной поверхности одного зерна заполнителя к его расчетной, определенной по выбранной зависимости. Следовательно, можно выразить: 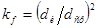 , здесь
, здесь 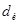 - средний истинный,
- средний истинный, 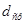 - средний расчетный диаметр зерен. С другой стороны, из условия постоянства величины общей поверхности зерен (
- средний расчетный диаметр зерен. С другой стороны, из условия постоянства величины общей поверхности зерен (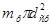 =
=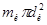 , где
, где 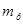 и
и 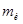 - расчетное и истинное количества зерен):
- расчетное и истинное количества зерен): 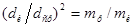 , а отсюда имеем довольно простое и удобное выражение коэффициента формы:
, а отсюда имеем довольно простое и удобное выражение коэффициента формы: 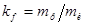 . В этой формуле расчетное количество зерен определяется на основании их средней крупности по следующей очевидной зависимости:
. В этой формуле расчетное количество зерен определяется на основании их средней крупности по следующей очевидной зависимости:
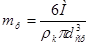 , (8)
, (8)
где 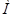 - масса испытываемого заполнителя.
- масса испытываемого заполнителя.
Приведем пример по определению коэффициента формы и удельной поверхности для зерен крупного заполнителя. В гравии Танхазского карьера, с плотностью 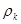 = 2,69 г/см3, средней крупностью
= 2,69 г/см3, средней крупностью 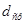 = 0,98 см количество зерен в одном килограмме составляло
= 0,98 см количество зерен в одном килограмме составляло 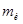 = 608 штук. Определяем
= 608 штук. Определяем 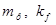 и
и 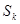 :
:
По формуле (8): 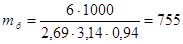 шт., коэффициент формы
шт., коэффициент формы 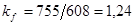 ; по формуле (6):
; по формуле (6): 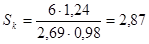 см2/г.
см2/г.
Второй способ определения параметра 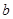 вытекает из самой структуры уравнения (1), а также из двух условий методики профессора Ю. М. Баженова [1] по определению водопотребности песка: 1-постоянства консистенции опытных растворов
вытекает из самой структуры уравнения (1), а также из двух условий методики профессора Ю. М. Баженова [1] по определению водопотребности песка: 1-постоянства консистенции опытных растворов 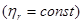 ; 2-постоянства величины песчано-цементного отношения
; 2-постоянства величины песчано-цементного отношения 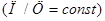 . Эти положения позволяют выразить параметр
. Эти положения позволяют выразить параметр 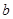 как функцию опытного водоцементного отношения, характеризующую, в свою очередь, водопотребность песка (
как функцию опытного водоцементного отношения, характеризующую, в свою очередь, водопотребность песка (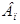 ).
).
Таблица 1
Значения параметра 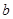 , рассчитанные по формулам (4), (10) при
, рассчитанные по формулам (4), (10) при 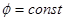
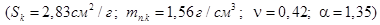 и по формуле
и по формуле 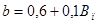
|
Характеристика песков |
Характеристика опытных замесов |
Параметр |
||||
|
Удельная поверхность |
Водопотребность |
|
|
По формуле (4) |
По формуле (10) |
По формуле |
|
55–60 |
6,4 |
1,8 2,1 |
17,5 28,0 |
1,28 |
1,21 |
1,24 |
|
85–90 |
8,8 |
1,5 1,8 |
17,2 30,0 |
1,52 |
1,49 |
1,48 |
|
110–120 |
11,3 |
1,3 1,6 |
18,0 32,0 |
1,67 |
1,73 |
1,73 |
|
160–170 |
14,7 |
1,0 1,3 |
13,8 29,0 |
2,07 |
2,04 |
2,07 |
На основании изложенного, используя формулу определения водопотребности песка, приведенную в работе [1], уравнение (3) можно выразить в виде:
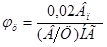 . (9)
. (9)
Подставляя значения 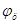 и
и 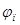 из зависимости (9) и (2) в уравнение (1) и принимая равными величины
из зависимости (9) и (2) в уравнение (1) и принимая равными величины 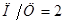 ;
; 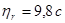 (по опытным данным), после некоторых преобразований находим параметр качества мелкого заполнителя в бетоне:
(по опытным данным), после некоторых преобразований находим параметр качества мелкого заполнителя в бетоне:
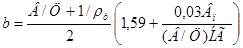 . (10)
. (10)
В таблице 1 приведено сравнение значений параметра 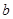 , вычисленных из зависимости (4) и (10) для песков различной крупности и водопотребности. Хорошее соответствие приведенных результатов на основе анализа консистенции бетонных смесей и растворов подтверждает применимость и равноценность обоих способов оценки качества мелкозернистых заполнителей при оптимизации составов бетона. Параметр
, вычисленных из зависимости (4) и (10) для песков различной крупности и водопотребности. Хорошее соответствие приведенных результатов на основе анализа консистенции бетонных смесей и растворов подтверждает применимость и равноценность обоих способов оценки качества мелкозернистых заполнителей при оптимизации составов бетона. Параметр 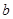 можно вычислить также по формуле
можно вычислить также по формуле 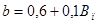 приведенной в работе [3], которая была получена на основе статистического анализа опытных данных методом корреляции. Как показывают расчетные сравнения, при этом имеет место практически одинаковые значения параметра
приведенной в работе [3], которая была получена на основе статистического анализа опытных данных методом корреляции. Как показывают расчетные сравнения, при этом имеет место практически одинаковые значения параметра 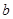 , вычисленные вышеуказанными способами.
, вычисленные вышеуказанными способами.
Зависимость (1) позволяет также учитывать влияние различных химических добавок на консистенции бетонных смесей. При этом их влияния проявляются в изменении нормальной густоты цементного теста.
Полученные зависимости (4) и (9) позволяют расширить область применения предложенного ранее [3] способа оптимизации составов бетона, включая нестандартные мелкозернистые пески.
Литература:
1. Баженов Ю. М. Технология бетона. — М.: АСВ, 2010. — 500 с.
2. Ахвердов А. Н. Основы физики бетона. — М.: Стройиздат, 1981. — 464 с.
3. Хуррамов Ш. Х., Авлакулов М. Реолого-технологические аспекты управления и оптимизации состава гидротехнического бетона. // Инновацион технологиялар.-Карши, 2014, № 4 — с. 30–34.







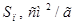
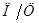
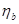 , с
, с