Эффективность работы технологических линий горно-металлургических предприятий в значительной мере определяется стабильностью рабочих режимов грунтовых насосов откачивающих пульпу. Однако при эксплуатации отмечается недостаточная долговечность грунтовых насосов, что вызывается повышенным гидроабразивным износом. Особенно этот недостаток проявляется при переработке сильноабразивных грунтов [1,2].
Для оценки эффективной работы грунтового насоса необходим показатель, учитывающий техническое состояние механизма и его возможности удовлетворять технологическим требованиям, а также экономическую целесообразность эксплуатации его в контролируемом режиме. Таким показателем может служить величина степени износа деталей насоса. Для определения величины степени износа деталей насоса воспользуемся методом планирования эксперимента, на основе которого создадим математическую модель степени износа грунтовых насосов.
Планирование эксперимента относится к одной из самых актуальных проблем научного исследования. основная цель научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную и определение, при каком сочетании уровней внешних и внутренних факторов может быть получена наиболее полная и достоверная информация о поведении системы [3].
Построение математической модели технологического процесса в зависимости от поставленной задачи [4,5] может преследовать следующие цели: минимизировать износ деталей насосов, улучшить показатели надежности и т. п.; увеличить надежность и быстродействие управления, увеличить эффективность контроля качества, создать условия для автоматизации процесса управления и т. п.
Целевой функцией выберем параметр износа деталей насоса 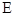 .
. 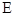 должен соответствовать следующим требованиям:
должен соответствовать следующим требованиям:
- параметр должен измеряться при любом изменении (комбинации) режимов технологического процесса;
- параметр должен быть статистически эффективным, то есть измеряться с наибольшей точностью;
- параметр должен быть информационным, то есть всесторонне характеризовать технологический процесс;
На основе опытных [1, 2, 6, 5] и анализа полученных нами данных выявлено, что интенсивность износа 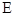 насосного агрегата является функцией
насосного агрегата является функцией
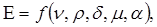 (1)
(1)
где факторы: 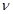 — скорость потока пульпы
— скорость потока пульпы 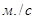 ;
; 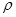 — плотность пульпы,
— плотность пульпы, 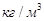 ;
; 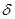 - предельная прочность изнашиваемого тела,
- предельная прочность изнашиваемого тела, 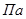 ;
;  — твердость частиц в пульпе,
— твердость частиц в пульпе, 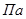 ;
; 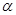 — угол атаки вектора скорости потока пульпы.
— угол атаки вектора скорости потока пульпы.
За фактор примем величину, характеризующую то или иное свойство объекта или режим технологического оборудования. Эта величина, числовое значение которой измеряется в пределах (границах) изменения, должна влиять на износ деталей насоса.
Описание исследуемого объекта нельзя получить в виде точной формулы функции, справедливой во всем диапазоне существования аргументов. Оно может быть лишь приближенным и на небольшом участке в окрестностях выбранной базовой точки. Аппроксимация искомой математической зависимости представляет собой полином — отрезок ряда Тейлора, в который разлагается неизвестная зависимость [7]

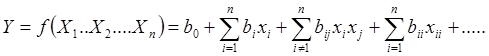 (2)
(2)
где
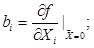
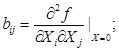
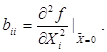
В силу наличия неуправляемых и даже неконтролируемых входных переменных 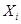 —
— 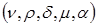 изменение величины Y
изменение величины Y 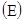 носит случайный характер, а потому уравнение (2) не дает нам точной связи между входом и выходом объекта и является лишь условным математическим ожиданием случайной величины Y, т. е. уравнением регрессии.
носит случайный характер, а потому уравнение (2) не дает нам точной связи между входом и выходом объекта и является лишь условным математическим ожиданием случайной величины Y, т. е. уравнением регрессии.
Коэффициенты уравнения регрессии определяются следующей системой уравнений
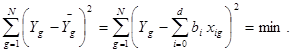 (3)
(3)
где 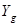 — экспериментальные значения выходного параметра, полученные в g-й точке факторного пространства; d — количество членов в уравнении регрессии.
— экспериментальные значения выходного параметра, полученные в g-й точке факторного пространства; d — количество членов в уравнении регрессии.
Выражение (3) является основным критерием проверки правильности найденного уравнения регрессии.
Система уравнений может быть представлена в виде матрицы, и необходимо, чтобы матрица была невырожденной, т. е. вектор — столбцы были линейно — независимы.
Матрица планирования должна отвечать следующим условиям [3]:
1. Ортогональность
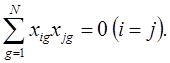
2. Условие нормированости
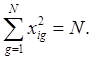
3. Симметричность относительно центра экстремума
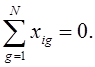
4. Координаты точек факторного пространства в матрице планирования должны подстраиваются так, что точность предсказания значения параметра оптимизации одинакова на равных расстояниях от центра эксперимента (базовой точки) и не зависит от направления.
Одним из важнейших положений современной теории планирования эксперимента является рандомизация. Поскольку многие условия проведения эксперимента могут измениться от опыта к опыту то, чтобы не возникали систематические смещения, следует рандомизировать, т. е. сделать случайными те систематически действующие факторы, которые трудно поддаются учету и контролю, для того, чтобы рассматривать их как случайные величины и учитывать статистически.
Матрица плана приведена в таблице 1.
Таблица 1
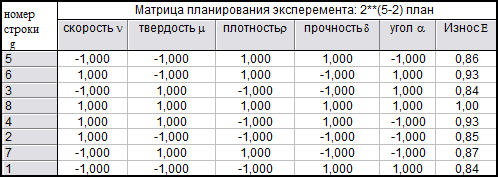
При проведении расчетов воспользуемся пакетом прикладного программного обеспечения «Statistica» версии 8.0.
В таблице 2 приведены результаты дисперсионного анализа. В таблице 3 приведены результаты оценки эффекта дисперсионного анализа.
Таблица 2
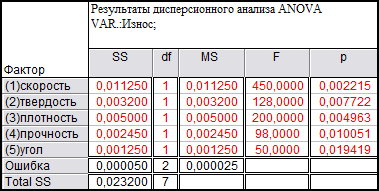
Таблица 3
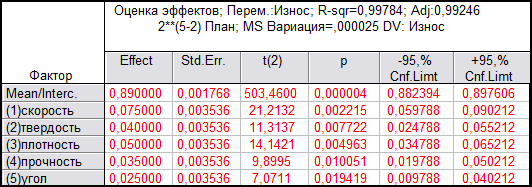
где
Effect — эффект значение вклада каждого фактора на износ насосного агрегата; Std. Error — Стандартная ошибка оценки эффекта; t(df) and p-value — значение t-критерия и уровня р; t-критерий используется для проверки гипотезы о равенстве нулю свободного члена; F — значения F-критерия; df — число степеней свободы F-критерия; p — уровень значимости; Coeff. — коэффициенты уравнения; Std. Err. Coeff. — стандартная ошибка коэффициентов (уравнения).
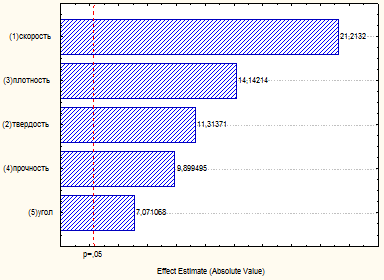
Рис. 1. Диаграмма Pareto стандартизированных эффектов; Переменная: Износ 2**(5–2) план; MS Residual=,000025
На рис. 1. приведена диаграмма Парето. На этой диаграмме оценки эффектов дисперсионного анализа расположены по абсолютной величине значений: от наибольших к наименьшим. Величина каждого эффекта представлена столбиком, и столбики пересекают линией, указывающей, каков должен быть эффект по величине (то есть какова должна быть длина столбика), чтобы быть статистически значимым. Из диаграммы можно сделать вывод, что все рассмотренные выше факторы значимы для модели износа насосного агрегата.
Решение задачи регрессионного анализа целесообразно разбить на несколько этапов: предварительная обработка; выбор вида уравнений регрессии; вычисление коэффициентов уравнения регрессии; проверка адекватности построенной функции результатам наблюдений.
Таблица 4
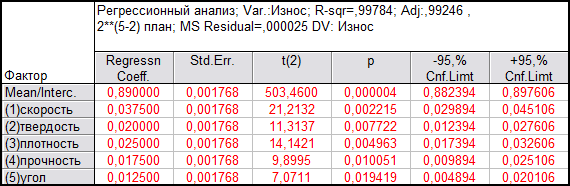
Таблица 5
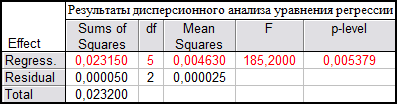
Результаты дисперсионного анализа уравнения регрессии представлены в таблицах 4 и 5. В строках таблицы дисперсионного анализа уравнения регрессии — источники вариации: Regress. — обусловленная регрессией, Residual- остаточная, Total — общая. В столбцах таблицы: Sums of Squares — сумма квадратов, df — число степеней свободы, Mean Squares — средний квадрат, F — значение F — критерия, p-level — вероятность нулевой гипотезы для F — критерия.
F — критерий полученного уравнения регрессии значим на 5 % уровне. Вероятность нулевой гипотезы (p-level) значительно меньше 0,05, что говорит об общей значимости уравнения регрессии.
Таким образом, в результате проведенного регрессионного анализа получено следующее уравнение степени износа насосного агрегата 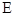 в функции скорости потока пульпы
в функции скорости потока пульпы 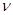 , твердости частиц в пульпе
, твердости частиц в пульпе  , плотности пульпы
, плотности пульпы 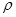 , прочности
, прочности 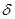 и углом атаки
и углом атаки 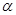
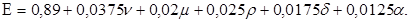 (4)
(4)
т. е. математическая модель степени износа грунтового насоса, которая аппроксимирована уравнением с исходным массивом данных, полученным в ходе эксперимента. Анализ соответствия модели исходным данным позволяет говорить о достаточной степени точности полученных результатов. Коэффициенты полученного в результате уравнения линейной регрессии оцениваются как значимые. Исследуемая модель оценивается как адекватная.
Литература:
1. Животовский Л. С., Смойловская Л. А. Техническая механика гидросмессей и грунтовые насосы. М.: Машиностроение, 1986. — 224с.
2. Супрун В. Н. Абразивный износ грунтовых насосов и борьба с ним. М. Машиностроение, 1972. — 104 с.
3. Адлер Ю. П., Маркова Е. В., Грановский Ю. В. Планирование эксперимента при поиске оптимальных условий. 2-е изд., перераб. и доп.- М.: Наука, 1976. — 280 с.
4. Методы и средства испытаний на трение и износ конструкционных и смазочных материалов: Справочник / B. C. Комбалов; под ред. К. В. Фролова. М.: Машиностроение, 2007. — 384с.
5. Островский В. Г., Пещеренко С. Н., Каплан А. Л. Методика моделирования гидроабразивного износа ступеней нефтяных насосов // Горное оборудование и электромеханика. — 2011, № 12, С. 38–42.
6. Тимухин С. А. Оптимизация рабочих процессов рудничных турбоустановок // Известия вузов. Горный журнал, 2004, № 1. с. 84–89.
7. Костин В. Н., Тишина Н. А. Статистические методы и модели: Учебное пособие. — Оренбург: ГОУ ОГУ, 2004. — 138 с.







