В статье приведены исследования осесимметричных колебаний кольцевого зернового слоя при движении по структурному цилиндрическому решету зерновых сепараторов, получены математические выражения.
Постановка проблемы. Математическое моделирование динамики движущихся зерновых смесей (ЗС) по плоским и цилиндрическим виброрешетам [1], как аналогия с жидкостью — псевдоожижение, показало свою адекватность.
В результате проведенных исследований разработана модель динамики пузырьковой псевдоожиженной ЗС по плоским структурным виброрешетам, которая показала свою эффективность [2–4]. Последующий анализ способов и выбор эффективного направления моделирования динамики пузырьковых псевдоожиженных зерновых смесей на цилиндрических виброрешетах с учетом структурности решет и свойств смеси позволит значительно расширить область применения предварительно полученных математических моделей.
Цель работы: исследования осесимметричных колебаний кольцевого зернового слоя при движении по структурному цилиндрическому решету зерновых сепараторов.
Основной материал. В результате исследований [5] получена начально-краевая задача, которая позволяет моделировать процесс просеваемости кольцевого зернового слоя в цилиндрических зерновых сепараторах.
Принимаем 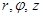 — цилиндрическою систему координат связанная с решетом. Поверхность решета представляет собой двумерно-периодическую структуру с периодом
— цилиндрическою систему координат связанная с решетом. Поверхность решета представляет собой двумерно-периодическую структуру с периодом 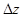 вдоль аксиальной координаты z и периодом
вдоль аксиальной координаты z и периодом 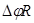 вдоль азимутальной координаты
вдоль азимутальной координаты 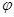 . Периодическая структура (решето) получается трансляцией базовой ячейки вдоль оси z и вдоль образующей цилиндрического решета, соответственно, на
. Периодическая структура (решето) получается трансляцией базовой ячейки вдоль оси z и вдоль образующей цилиндрического решета, соответственно, на 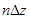 и
и 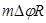 , где
, где 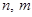 — целые числа. Принимаем
— целые числа. Принимаем 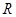 - радиус цилиндрической поверхности решета, а
- радиус цилиндрической поверхности решета, а 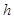 - толщина кольцевого слоя зерновой смеси.
- толщина кольцевого слоя зерновой смеси.
В [6] получены упрощенные уравнения динамики пузырькового псевдоожиженого зернового слоя
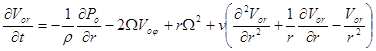 , (1)
, (1)
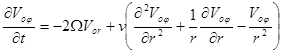 , (2)
, (2)
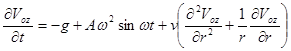 , (3)
, (3)
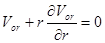 . (4)
. (4)
Построение решения уравнений (1) — (4) будем осуществлять с помощью преобразования Лапласа по временной переменной 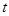 . Пусть
. Пусть 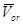 ,
, 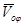 ,
, 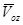 и
и 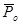 — преобразования Лапласа
— преобразования Лапласа 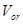 ,
, 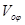 ,
,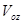 и
и 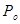 :
:
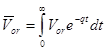 ,
, 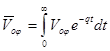 ,
, 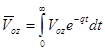 ,
, 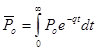 . (5)
. (5)
Применим к уравнениям (1) — (4) преобразования Лапласа и используя обозначения (5) получим:
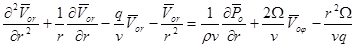 , (6)
, (6)
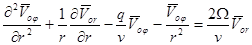 , (7)
, (7)
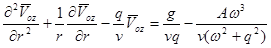 , (8)
, (8)
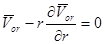 . (9)
. (9)
Из уравнения (9) имеем: 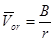 , (10)
, (10)
где 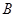 — величина зависящая только от параметра
— величина зависящая только от параметра 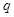 преобразования Лапласа.
преобразования Лапласа.
Подставим (10) в уравнения (6) и (7). Тогда получим
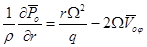 , (11)
, (11)
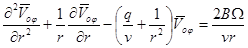 . (12)
. (12)
Общее решение уравнения (12) имеет вид:
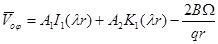 , (13)
, (13)
где 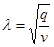 ,
, 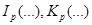 — модифицированные бесселевые функции первого и второго рода [7],
— модифицированные бесселевые функции первого и второго рода [7], 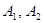 — величины независящие от переменной
— величины независящие от переменной 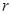 .
.
Для определения величин 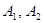 подставим (13) в краевые условия:
подставим (13) в краевые условия: 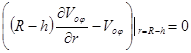 и
и 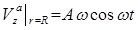 ,
, 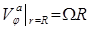 , где
, где 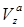 и
и 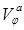 — тангенциальные к поверхности решета компоненты абсолютной скорости
— тангенциальные к поверхности решета компоненты абсолютной скорости 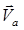 .
.
Тогда после ряда преобразований будем иметь:
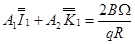 , (14)
, (14)
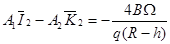 , (15)
, (15)
где 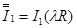 ,
, 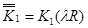 ,
, 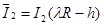 ,
, 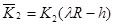 .
.
Определяя из (14), (15) 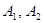 и подставляя их в (13) получаем следующее выражение для
и подставляя их в (13) получаем следующее выражение для 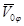 :
:
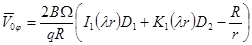 , (16)
, (16)
где 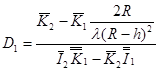 ,
, 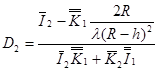 . (17)
. (17)
Далее из уравнения (11) с учетом (16), (17) имеем:
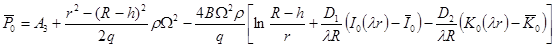 , (18)
, (18)
где 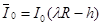 ,
, 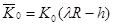 ,
, 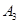 - некоторая константа.
- некоторая константа.
Для определения 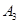 достаточно подставить (18) в краевое условие
достаточно подставить (18) в краевое условие 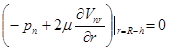 , из которого получаем:
, из которого получаем: 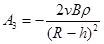 .
.
Рассмотрим теперь уравнение (8). Общее решение этого уравнения является суммой частного решения и общего решения однородного уравнения (в (8) правая часть равна нулю). Общее решение однородного уравнения можно представить с помощью модифицированных бесселевых функций в следующем виде:
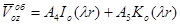 , (19)
, (19)
где 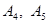 — величины зависящие от переменной r,
— величины зависящие от переменной r, 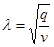 .
.
Частное решение уравнения (8) построим с помощью метода вариации постоянных [7]. В соответствии с этим методом частное решение ищем в виде:
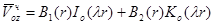 . (20)
. (20)
Здесь 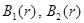 — некоторые неизвестные функции.
— некоторые неизвестные функции.
Для нахождения этих функций имеем следующую систему уравнений:
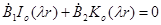 ,
,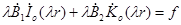 , (21)
, (21)
где 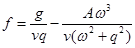 , а точка обозначает операцию дифференцирование по аргументу.
, а точка обозначает операцию дифференцирование по аргументу.
Из (21), после ряда преобразований получаем:
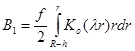 ,
, 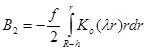 . (22)
. (22)
Для вычисления интегралов в (22) используем следующие рекуррентные формулы [7]:
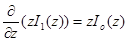 ,
, 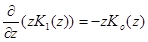 .
.
Тогда будем иметь:
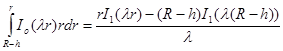 , (23)
, (23)
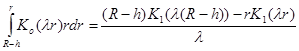 .
.
С помощью (23), окончательно получим следующее выражение для общего решения уравнения (8):
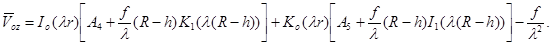 (24)
(24)
Для определения величин 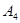 и
и 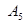 воспользуемся краевыми условиями на свободной поверхности зернового слоя и внутренней поверхности виброрешета.
воспользуемся краевыми условиями на свободной поверхности зернового слоя и внутренней поверхности виброрешета.
Из 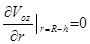 получаем:
получаем: 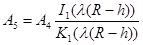 . (25)
. (25)
Подставим (25) в (24). Тогда из краевого условия на внутренней поверхности виброрешета имеем:
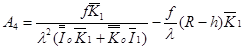 . (26)
. (26)
Здесь введены обозначения:
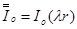 ,
, 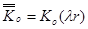 ,
, 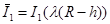 ,
, 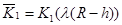 . (27)
. (27)
Учитывая (25) и (26), окончательно получаем
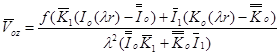 . (28)
. (28)
Таким образом, решение уравнений (6) — (9) имеет следующий вид
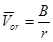 ,
, 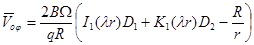 ,
,
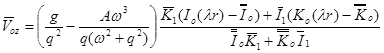 , (29)
, (29)
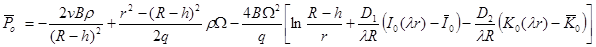 ,
,
где 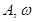 — амплитуда и круговая частота осевых колебаний решета,
— амплитуда и круговая частота осевых колебаний решета, 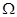 — угловая скорость вращения решета вокруг оси
— угловая скорость вращения решета вокруг оси 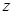 ,
, 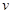 — кинематический коэффициент вязкости псевдожидкости c пузырьками, величины
— кинематический коэффициент вязкости псевдожидкости c пузырьками, величины 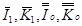 определяются по формулам (27), и величины
определяются по формулам (27), и величины 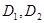 — по формуле (17).
— по формуле (17).
Выводы. Таким образом, получены упрощенные уравнения динамики псевдоожиженой зерновой смеси по цилиндрическому структурному решету зерновых сепараторов.
Литература:
1. Тищенко Л. Н., Мазоренко Д. И., Пивень М. В., Харченко С. А., Бредихин В. В., Мандрыка А. В. Моделирование процессов зерновых сепараторов. — Харьков: «Місьдрук», 2010. — 360 с.
2. Харченко С. А. К построению уравнений динамики стационарных потоков в псевдоожиженном зерновом слое на структурных виброрешетах / Харченко С. А. // Вісник ХНТУСГ: Механізація сільськогосподарського виробництва. — Харків:ХНТУСГ, 2014. — С.181–186.
3. Харченко С. А. Построение решений уравнений динамики зерновых смесей на плоских виброрешетах / Харченко С. А. // Конструювання, виробництво та експлуатація с. г. машин, вип.43, ч.ІІ.- Кіровоград: КНТУ, 2013. — С.287–292.
4. Харченко С. А. К построению трехмерной гидродинамической модели динамики пузырьковой псевдоожиженой зерновой смеси по структурному виброрешету / С. А. Харченко // Праці ТДАТУ. — Мелітополь, 2014. — Вип.14. Т.2. — С.80–85.
5. Харченко С. А. К разработке гидродинамической модели движения зерновой смеси по цилиндрическому решету виброцентробежных сепараторов // Вісник ХНТУСГ «Технічний сервіс машин для рослинництва». — Харків, 2015. — Вип. 159. — С.60–69.
6. Харченко С. А. Осесимметричные колебания кольцевого зернового слоя при движении по структурному решету // Вісник ХНТУСГ «Ресурсозберігаючі технології, матеріали та обладнання у ремонтному виробництві». — Харків, 2015. — Вип. № 158. — С.72–80.
7. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1970. — 720с.







