В процессе преподавания курса математического анализа студентам экономических специальностей часто приходится сталкиваться с непониманием необходимости изучения многих разделов. Преодолеть такого рода проблемы помогает демонстрация приложений изучаемого раздела. При изучении производной функции одной переменной это можно осуществить, рассматривая примеры приложения производной в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем.
Студентам можно показать, что один из основных законов теории производства звучит следующим образом: оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода. То есть уровень выпуска x0 является оптимальным для производителя, если MS(x0)=MD(x0), где MS — предельные издержки, а MD — предельный доход.
За C(x) обозначим функцию прибыли, тогда C(x)=D(x)-S(x). Следовательно, оптимальным уровнем производства является тот, при котором прибыль максимальна, т. е. такое значение выпуска x0, при котором функция C(x) имеет экстремум (максимум). По теореме Ферма в этой точке 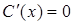 . Но C¢(x)=D¢(x)-S¢(x), поэтому D¢(x0)=S¢(x0), т. е. MD(x0)=MS(x0).
. Но C¢(x)=D¢(x)-S¢(x), поэтому D¢(x0)=S¢(x0), т. е. MD(x0)=MS(x0).
Другое важное понятие теории производства — это уровень наиболее экономичного производства, при котором средние издержки по производству товара минимальны. Соответствующий экономический закон гласит: уровень наиболее экономичного производства определяется равенством средних и предельных издержек.
Получим это условие как следствие теоремы Ферма. Средние издержки AS(x) определяются как 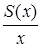 , т. е. издержки по производству товара, деленные на произведенное его количество. Минимум этой величины достигается в критической точке функции y=AS(x), т. е. при условии:
, т. е. издержки по производству товара, деленные на произведенное его количество. Минимум этой величины достигается в критической точке функции y=AS(x), т. е. при условии:
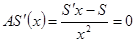 , откуда
, откуда 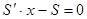 или
или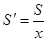 , т. е. MS(x)=AS(x).
, т. е. MS(x)=AS(x).
Свою интерпретацию в экономической теории находит понятие выпуклости функции. Один из наиболее знаменитых экономических законов — закон убывающей доходности — звучит следующим образом: с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т. д.), с некоторого момента убывает.
Иначе, величина 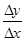 , где Dx — приращение ресурса, а Dy — приращение выпуска продукции, уменьшается при увеличении x. Таким образом, закон убывающей доходности формулируется так: функция y=f(x), выражающая зависимость выпуска продукции от вложенного ресурса, является функцией, выпуклой вверх.
, где Dx — приращение ресурса, а Dy — приращение выпуска продукции, уменьшается при увеличении x. Таким образом, закон убывающей доходности формулируется так: функция y=f(x), выражающая зависимость выпуска продукции от вложенного ресурса, является функцией, выпуклой вверх.
Другим базисным понятием экономической теории является функция полезности U=U(x), где x — товар, U — полезность. Эта величина очень субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Закон убывающей полезности звучит следующим образом: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента убывает. Очевидно, этот закон можно переформулировать так: функция полезности является функцией, выпуклой вверх. В такой постановке закон убывающей полезности служит отправной точкой для математического исследования теории спроса и предложения.
Теоретический анализ разнообразных явлений экономики использует ряд предельных величин. Перечислим лишь некоторые: предельные издержки, предельный доход, предельная склонность к потреблению и т. д. Все эти величины самым тесным образом связаны с понятием производной. В качестве характерного примера рассмотрим предельные издержки.
Пусть q — количество произведенной продукции, C(q) — соответствующие данному выпуску издержки. Предельные издержки обозначаются MC и определяются как дополнительные издержки, связанные с производством еще одной единицы продукции.
Другими словами,
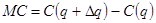 , где Dq=1.
, где Dq=1.
Используя равенство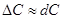 , получим
, получим
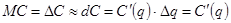 .
.
Таким образом, данное выше определение MC, по существу, не противоречит другому распространенному определению, согласно которому 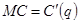 .
.
Рассмотриваем пример. Пусть C(q)=1500q-2q2+0,002q3. Тогда дополнительные издержки, связанные с увеличением выпуска от q до q+1, составят DC=C(q+1)-C(q), что приближенно равно
C¢(q)=1500–4q+0,006q2.
В таблице 1 даны значения DC и C¢(q) в точках q=100, 200,…, 1000.
Таблица 1
|
q |
C¢ |
DC |
|
100 |
1160 |
1158,6 |
|
200 |
940 |
939,2 |
|
300 |
840 |
839,8 |
|
400 |
860 |
860,4 |
|
500 |
1000 |
1001,0 |
|
600 |
1260 |
1261,6 |
|
700 |
1640 |
1642,2 |
|
800 |
2140 |
2142,8 |
|
900 |
2760 |
2763,4 |
|
1000 |
3500 |
3504,0 |
Общая схема введения предельных величин такова: пусть величина Yявляется функцией от величины X, тогда предельная величина MY(по X) определяется как отношение 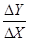 . Приращение DX в различных случаях задается по-разному. В одних случаях DX — это наиболее естественная единица измерения величины X, в других случаях DX — это разность между соседними значениями X в таблице, задающей функцию Y от X. В теоретических вопросах, однако, более удобным является определение MY, основанное на равенстве
. Приращение DX в различных случаях задается по-разному. В одних случаях DX — это наиболее естественная единица измерения величины X, в других случаях DX — это разность между соседними значениями X в таблице, задающей функцию Y от X. В теоретических вопросах, однако, более удобным является определение MY, основанное на равенстве
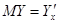 .
.
Конечно, при таком определении приходится дополнительно предполагать, что Yявляется дифференцируемой функцией от X.
Для исследования экономических процессов и решения прикладных задач используется понятие эластичности функции. Это понятие является чисто математическим и может применяться при анализе любых дифференцируемых функций.
Эластичностью функции y=f(x) в точке x0 называется следующий предел:
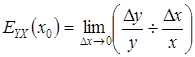 . (1)
. (1)
Говорят также, что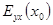 – это коэффициент эластичности y по x.
– это коэффициент эластичности y по x.
Из определения эластичности следует, что при достаточно малых Dxвыполняется приближенное равенство
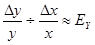 .
.
Эластичность Ey — это коэффициент пропорциональности между относительными изменениями величин y и x. Если, например, x увеличится на один процент, то y увеличивается (приближенно) на Ey процентов.
Заметим, что
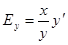 . (2)
. (2)
Таким образом, если x0¹0, то f(x0)¹0, для существования конечного предела (1) в точке x0 необходимо и достаточно, чтобы существовала конечная производная f¢(x0). Представим отношение 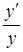 как логарифмическую производную. Соответственно, формула (2) запишется тогда в виде
как логарифмическую производную. Соответственно, формула (2) запишется тогда в виде
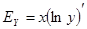 . (3)
. (3)
Далее рассматриваем свойства эластичности:
1. Эластичность в точке x0 суммы y=y1+…+yn положительных функций 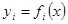 (i =1,2,…,n) удовлетворяет соотношению
(i =1,2,…,n) удовлетворяет соотношению 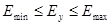 , где
, где 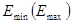 — это минимальная (максимальная) эластичность в точке x0 функции yi.
— это минимальная (максимальная) эластичность в точке x0 функции yi.
2. Эластичность произведения функций U=U(x) и V=V(x) в точке x0 равна сумме эластичностей функций U и V в той же точке:
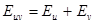 .
.
3. Эластичность частного функций U=U(x) и V=V(x) в точке x0 (V(x0) ¹0) равна разности эластичностей функций U и V в той же точке:
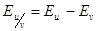 .
.
4. Для функций y=f(x) и x=g(t) эластичность y по t в точке t0 удовлетворяет следующему равенству:
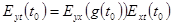 .
.
5. Для функции y=f(x) эластичность обратной функции x=g(y) в точке y0 удовлетворяет соотношению:
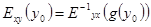 .
.
После этого на примерах рассматриваем нахождение эластичности функции.
1. Пусть y=C-const. Используя формулу (2), получим
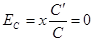 .
.
2. Пусть эластичность функции y=x+C, C — const.
По формуле (2) получаем
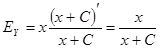 .
.
3. Найти эластичность степенной функции 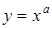 .
.
Применяя форму (3), находим эластичность
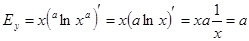 .
.
Практика преподавания показывает, что демонстрация возможности применения производной функции одной переменной в экономической теории способствует усилению мотивационной составляющей учебного процесса, существенным образом влияет на усвоение студентами данного раздела математического анализа и подготавливает студентов к дальнейшей профессиональной деятельности.
Литература:
1. Гудкова В. С., Ячинова С.Н, Новичкова Т. Ю. Наглядность как средство повышения качества обучения математике // Вестник магистратуры. — 2014. — № 12–4 (39). — С.41–43.
2. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах // Молодой ученый. — 2013. — № 12 (59). — С. 3–6.
3. Куимова Е. И., Куимова К. А., Ячинова С. Н. Формирование мотивационной составляющей обучения на примере изучения дифференциальных уравнений // Молодой ученый. — 2014. — № 2(61) — С.775–777.
4. Куимова К. А., Куимова Е. И., Ячинова С. Н. Профессиональная подготовка экономистов посредством решения оптимизационных задач // Молодой ученый. — 2014. — № 15 — С. 282–286.
5. Ячинова С. Н., Гудкова В. С. Мотивация обучения студентов посредством моделирования // Молодой ученый. — 2014. — № 4 — С.1141–1144.







