Работа посвящена разработке методики моделирования динамики процесса взрывного разложения микрокристаллов азида серебра при нелокальном характере стадии развития цепи. Моделирование процесса учитывает перенос энергии химической реакции по кристаллической решетке образца, который приводит к перераспределению концентраций реагентов в кристалле. Оптимальной областью для развития твердофазной цепной реакции является центр кристалла.
Ключевые слова: математическое моделирование, разностная схема, модель цепной реакции, взрывное разложение, перенос энергии, энергетические материалы, азид серебра.
The aim of this work is to work out the method of the simulation of the explosive decomposition process in the silver azide crystal taking into account that the chain propagation stage are nonlocal. The method includes calculation of the energy transfer among the lattice, what causes the redistribution of the reagents in the crystal. The optimal area for the solid state reaction to develop is the centre of the crystal.
Keywords: Simulation, difference scheme, chain reaction model, explosive decomposition, energy transfer, energetic material, silver azide
Задачей математического моделирования физико-химического процесса является одновременное рассмотрение химических превращений и физических процессов, среди последних наибольшее значение имеют диффузия продуктов реакции, промежуточных продуктов и исходных веществ, поглощение и передача энергии [1, c. 375, 2, c. 98]. Определение режимов и механизмов распространения реакции взрывного разложения энергетических материалов имеет большое прикладное значение, поскольку несанкционированное срабатывания исполнительных устройств различного назначения на основе взрывчатых веществ приводит к большому материальному ущербу [3, c. 14, 4, c. 63]. Актуальность исследования определяется кроме того необходимостью разработки оптических детонаторов [5] на основе инициирующих [6, c. 6, 7, c. 471] и вторичных взрывчатых веществ [8, c. 342, 9, c. 99]. Существуют два основных подхода к описанию процесса взрывного разложения энергетических материалов: с позиции моделей теплового [10, c. 805, 11, c. 45] и цепного взрывов [12, c. 42, 13, c. 15]. В рамках первого подхода предполагается разложение вещества по одностадийной реакции [14, c. 195, 15, c. 685], константа скорости которой имеет аррениусовскую температурную зависимость [16, c. 69, 17, c. 216]. В моделях цепного взрыва реализация самоускоряющегося режима разложения связана с размножением реагентов (переносчиков цепи) [18, c. 97, 19, c. 53].
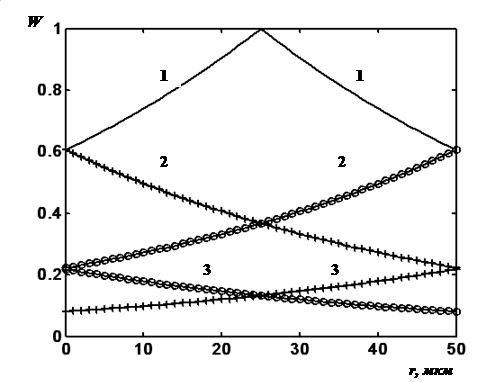
Рис. 1. Вероятность генерации e. h. пар (W) в кристалле азида серебра r = 50 мкм: 1 — при первом прохождении энергии химической реакции через кристалл, 2 –после первого, 3 — после второго отражения от граней кристалла
С позиций моделей цепного взрыва был объяснен ряд закономерностей взрывного разложения кристаллов азида серебра (АС) импульсом неодимового лазера, предложена феноменологическая модель процесса распространения реакции взрывного разложения АС [20, c. 23, 21, c. 38]. Целью настоящей работы является формулировка методики моделирования динамики процесса при нелокальном характере стадии развития цепи (феноменологическая модель распространения взрывного разложения АС) с учетом реальной геометрии кубических микрокристаллов.
Модель взрывного разложения азида серебра
Согласно феноменологической модели распространения взрывного разложения азиде серебра энергия химической реакции может эффективно передаваться кристаллической решетке с генерацией e. h. пар [20, c. 22, 22, c. 130]. Вероятность генерации электронных возбуждений является максимальной в непосредственной близости от области протекания реакции и экспоненциально снижается при увеличении расстояния от этой области:
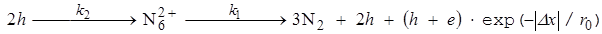 ,
,
где k1 — константа скорости распада комплекса N6, k2 — константа скорости образования комплекса N6. Стадия развития цепи взаимодействие двух радикалов N30 (h), локализованных в соседних узлах кристаллической решетки. Константа скорости реакции образования N6 оценивалась с учётом кулоновского отталкивания дырок, Дебаевского экранирования и тунелирования и составляет — k2 = 0.5·10–11 см-3с-1 [23, c. 13]. Комплекс N6 распадается на молекулярный азот (N2) — k1 = 3·107 с-1 [24, c. 19]. Выделившаяся энергия запасается на электронно и колебательно возбуждённых степенях свободы молекул азота. В рамках модели дипольного взаимодействия с электронной подсистемой кристалла оценены константы скоростей дезактивации с образованием электронно-дырочной пары (ke~ 109 с‑1) и передачей энергии зонной дырке (kν~ 10‑12 см3с‑1) [24, c. 19]. При дезактивации молекул азота происходит генерация активных частиц — стадия ветвления цепи происходит не только в реакционной зоне, но с вероятностью ~exp(-x/r0) вне неё. Величина r0 принимается равной ее экспериментальному значению 50 ± 10 мкм [20, c. 22, 22, c. 130]. Интенсивность стадии зарождения цепи определяется освещенностью внутри образца [25, c. 120, 26, c. 126, 27, c. 750], и в рамках данной работы не рассматривается.
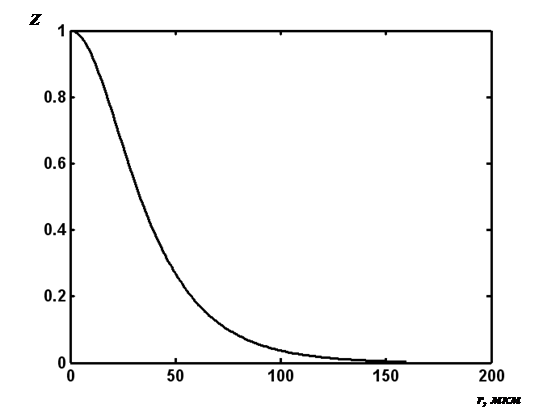
Рис. 2. Зависимость отношения вероятности генерации e-h пар в центре кристалла к вероятности их генерации на границе образца (Z) от размера кристалла (r)
Рассмотрим кубический микрокристалл азида серебра, подвергаемый действию импульсного лазерного излучения. Разделим образец на kn одинаковых ячеек. Протекание реакции в ячейке n влияет на концентрацию частиц во всех остальных ячейках, оценка степени этого влияния необходима на всех этапах расчета. Оценка данного влияния эквивалентна действию оператора L1 на функцию концентраций: f(xm)=L1f(xn). В основе решения задачи лежит процедура вычисления элементов матрицы, которая связывает выделение энергии в n-ой ячейке с генерацией носителей в ячейке m в зависимости от размеров микрокристалла.
Так как существует вероятность генерации e. h. пар на поверхности образца, то возможно отражение энергии от грани кристалла аналогично упругому и неупругому отражению. При «упругом» (зеркальном) отражении (проявляющемся лишь в инвертировании знака нормальной к отражающей поверхности составляющей импульса) изменяется направление передачи энергии, которая в дальнейшем расходуется на генерацию электронных возбуждений в объеме кристалла. Согласно модели происходит многократное «упругое» отражение с одновременным линейным поглощением энергии реакции. В этом случае можно рассматривать процесс как совокупность отдельных ветвей отражения энергии: первая ветвь — распределение вероятности генерации e. h. пар от места протекания реакции до границы образца, вторая и далее — от одной грани кристалла до другой, и в дальнейшем суммировать вероятности. На рис. 1. представлена рассчитанная вероятность генерации e. h. пар (W) в кристалле азида серебра r = 50 мкм. 1 — при первом прохождении энергии химической реакции через кристалл, 2 –после первого, 3 — после второго отражения от граней кристалла. Такое предположение обосновано, если реализуются два предположения: все направления отражения в твердом теле считаются равновероятными, а свойства частиц приповерхностного слоя изотропными; учет энергопотерь на поверхности осуществляется только за счет рекомбинационной составляющей. На рис. 2 представлена зависимость величины отношения вероятности генерации носителей цепи в центре кристалла на аналогичную величину для поверхности образца от размера кристалла. Для кристаллов размерами r > 200 мкм достаточным оказывается учет только первой и второй ветвей. В области размеров 30 мкм < r < 200 мкм необходим учет первой — шестой ветвей. При r < 30 мкм отношение вероятностей генерации на границе и центре кристалла практически одинаковы, в этом случае распределение генерации электронных возбуждений по кристаллу можно считать равномерным.
Результаты и выводы
Нелокальность акта ветвления цепи приводит к значительному перераспределению активных частиц только в больших кристаллах. Концентрация активных частиц, генерируемых по этому каналу, экспоненциально спадает вне области протекания реакции. Генерация активных частиц при этом происходит симметрично во все стороны от облучаемой области. Оптимальной областью для развития твердофазной цепной реакции является центр кристалла. Работа выполнена при финансовой поддержке РФФИ (грант № 14–03–00534 А), Министерства образования и науки РФ (госзадание № 2014/64) и Российского научного фонда.
Литература:
1. Кригер, В. Г. Процессы теплопереноса при лазерном разогреве включений в инертной матрице / В. Г. Кригер, А. В. Каленский, А. А. Звеков, И. Ю. Зыков, А. П. Никитин // Теплофизика и аэромеханика. — 2013. — Т.20. — № 3. — С.375–382.
2. Каленский, А. В. Влияние длины волны лазерного излучения на критическую плотность энергии инициирования энергетических материалов / А. В. Каленский, А. А. Звеков, М. В. Ананьева и др. // Физика горения и взрыва. –2014. — Т. 50. — № 3. — С. 98–104.
3. Ananyeva, M. V. Comparative analysis of energetic materials explosion chain and thermal mechanisms / M. V. Ananyeva, V. G. Kriger, A. V. Kalensii and others // Известия высших учебных заведений. Физика. — 2012. — Т.55. — № 11–3. — С. 13–17.
4. Kalenskii, A. V. The Microcenter Heat Explosion Model Modernization / A. V. Kalenskii, V. G. Kriger, A. A. Zvekov and others // Известия ВУЗов. Физика. — 2012. — Т. 55. — № 11/3. — С.62–66.
5. Кригер, В.Г., Каленский А. В., Ананьева М. В., Звеков А. А. Способ регулирования порога инициирования оптического детонатора/ В. Г. Кригер, А. В. Каленский, М.В Ананьева и др.//патент на изобретение RUS 2538263 18.11.2014.
6. Ананьева, М. В. Перспективные составы для капсюля оптического детонатора / М. В. Ананьева, А. А. Звеков, И. Ю. Зыков и др.// Перспективные материалы. — 2014. — № 7. — С. 5–12.
7. Ananyeva, M. V. The size effects and before-threshold mode of solid-state chain reaction / M. V. Ananyeva, A. V. Kalensii // Журнал Сибирского федерального университета. Серия: Химия. — 2014. — Т. 7. — № 4. — С. 470–479.
8. Каленский, А. В. Спектральная зависимость критической плотности энергии инициирования композитов на основе пентаэритриттетранитрата с наночастицами никеля / А. В. Каленский, М. В. Ананьева, А. А. Звеков и др.// Фундаментальные проблемы современного материаловедения. — 2014. — Т.11. — № 3. — С. 340–345.
9. Адуев, Б. П. Микроочаговая модель лазерного инициирования взрывного разложения энергетических материалов с учетом плавления / Б. П. Адуев, М. В. Ананьева, А. А. Звенков и др. // Физика горения и взрыва. — 2014. — Т. 50. — № 6. — С. 92–99.
10. Kalenskii, A. V. Spectral regularities of the critical energy density of the pentaerythriol tetranitrate -aluminium nanosystems initiated by the laser pulse / A. V. Kalenskii, M. V. Ananyeva // Наносистемы: физика, химия, математика. — 2014. — Т. 5. — № 6. — С. 803–810.
11. Гришаева, Е. А. Неизотермическая модель разветвленной цепной реакции взрывного разложения энергетических материалов / Е. А. Гришаева, А. В. Каленский, М. В. Ананьева и др.// Фундаментальные проблемы современного материаловедения. — 2013. — Т.10. — № 1. — С. 44–49.
12. Боровикова, А. П. Природа стадии обрыва цепи разветвленных твердофазных цепных реакций / А. П. Боровикова, М. В. Ананьева, О. В. Одинцова// Молодой ученый. — 2014. — № 15(74). — С. 41–45.
13. Кригер, В. Г. Механизм твердофазной цепной реакции/ В. Г. Кригер, А. В. Каленский, Ю. А. Захаров и др. // Материаловедение. — 2006. — № 9. — С. 14–21.
14. Ананьева, М. В. Кинетические закономерности взрывного разложения ТЭНа, содержащего наноразмерные включения алюминия, кобальта и никеля / М. В. Ананьева, А. В. Каленский, Е. А. Гришаева и др. // Вестник КемГУ. — 2014. — № 1–1(57). — С. 194–200.
15. Zvekov, A. A. Regularities of light diffusion in the compo site material pentaery thriol tetranitrate — nickel / A. A. Zvekov, M. V. Ananyeva, A. V. Kalenskii and others // Наносистемы: физика, химия, математика. — 2014. — Т. 5. — № 5. — С. 685–691.
16. Никитин, А. П. Расчет критических параметров инициирования теплового взрыва тэна с наночастицами меди на разных длинах волн / А. П. Никитин // Международное научное издание Современные фундаментальные и прикладные исследования.– 2013. — № 4(11).– С. 68–75.
17. Звеков, А. А. Расчет оптических свойств композитов пентаэритрит тетранитрат — наночастицы кобальта/ А. А. Звеков, А. В. Каленский, Б. П. Адуев и др.// Журнал прикладной спектроскопии. — 2015. — Т. 82. — № 2. — С. 215–222.
18. Боровикова, А. П. Методика моделирования распространения взрывного разложения азида серебра / А. П. Боровикова, А. В. Каленский// Аспирант. — 2014. — № 4. — С. 96–100.
19. Ананьева, М. В. Инициирование взрывного разложения микрокристаллов азида серебра / А. В. Каленский, М. В. Ананьева // Молодой ученый. — 2014. — № 19. — С. 52–55.
20. Кригер, В. Г. Определение пространственных характеристик волны цепной реакции в азиде серебра / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Химическая физика. — 2014. — Т. 33. — № 8. — С. 22–29.
21. Боровикова, А. П. Пространственно-временные характеристики волны горения в азиде серебра / А. П. Боровикова, А. В. Каленский, И. Ю. Зыков// Аспирант. — 2014. — № 3. — С. 37–42.
22. Кригер, В. Г. Определение ширины фронта волны реакции взрывного разложения азида серебра / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Физика горения и взрыва. — 2012. — Т.48. — № 4. — С 129–136.
23. Каленский, А. В. Коэффициент захвата электронных носителей заряда на экранированном отталкивающем центре/ А. В. Каленский, М. В. Ананьева, В. Г. Кригер, А. А. Звеков// Химическая физика. — 2014. — Т. 33. — № 4. — С. 11–16.
24. Кригер, В. Г. Релаксация электронно-возбужденных продуктов твердофазной реакции в кристаллической решетке / В. Г. Кригер, А. В. Каленский, А. А. Звеков // Химическая физика. — 2012. — Т.31. — № 1. — С. 18 - 22.
25. Каленский А. В. Кинетические закономерности взрывчатого разложения таблеток тетранитропентаэритрит-алюминий / А. В. Каленский, А. А. Звеков, М. В. Ананьева и др. // Журнал технической физики. — 2015. — Т. 85. № 3. — С. 119–123.
26. Адуев, Б. П. Исследование оптических свойств наночастиц алюминия в тетранитропентаэритрите с использованием фотометрического шара / Б. П. Адуев, Д. Р. Нурмухаметов, Г. М. Белокуров и др. // Журнал технической физики. — 2014. — Т. 84. — № 9. — С. 126–131.
27. Звеков, А. А. Моделирование распределения интенсивности в прозрачной среде с Френелевскими границами, содержащей наночастицы алюминия / А. А. Звеков, А. В. Каленский, А. П. Никитин и др.// Компьютерная оптика. — 2014. — Т. 38. — № 4. — С. 749–756.







