В данной работе исследуются системы нелинейных дифференциальных уравнений высоких порядка вида
, (1)
где х, f-n-мерные векторы,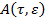 
– действительная квадратная матрица порядка 
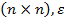-малый параметр, 
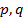— натуральные числа и такие что 
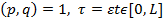-медленные время, 
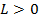фиксированное число.
Известна, что структура формальных, в смысле [1] частных решений системы (1) тесно связано о поведением корней так называемого характеристического уравнения
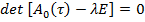, (2)
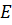-единичная матрица порядка 
.
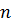В настоящей работе рассматриваетcя вопрос построения формальных частных решения системы (1) при наличии нулевого корня характеристического уравнения (2), т. е. так называемый критический случай [2]. Этот случай, а также случай, от отличных от нуля корней уравнения (2) для системы нелинейных дифференциальных уравнения высокого порядка в литературе не рассматривалась.
По этому несомненно представляет определенный интерес исследование системы вида (1). В дальнейшем будем считать, что выполняютcя условия:
1) матрица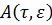 
допускают разложения:
2) матрицы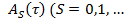
при 
, а вектор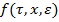 
в область 
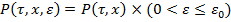, где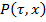 
некоторая область пространства переменных 
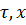, неограниченно дифференцируемых;
3) при , 
, 
, 
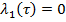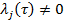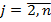(4)
4) 
, 
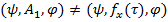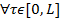, где 
, 
, 
.
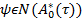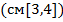Для удобства в системе (1) введем замену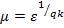 
.
Тогда системы (1) запушатся в виде
(5)
Теорема 1. Если выполняются условия 1–4, то система дифференциальных уравнений (5) имеет формальные частные решение вида
Доказательство. В зависимости между числом p и q рассмотрим две случае 1) p>q; 2) p<q. Доказательство теорема приведём для случая p>q, а для случая p<q теоремы доказывается аналогично. Поставляя (6) в системы (5) и учитывая разложения вектор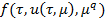 
в ряд Тейлора в окрестности точки 
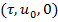получим
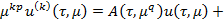
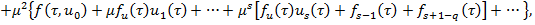
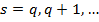(7)
где элементы матрицы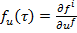 
и координаты вектор 
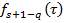вычисляются в точке 
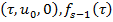выражаются определенным образом через 
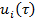(i=1,2,3, …, s–1).
Если в тождестве (7) приравняем коэффициенты при одинаковых степеням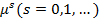 
, то получим следующую систему уравнений для определения неизвестных 
:
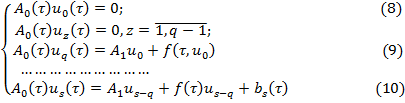
где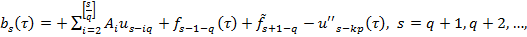 
при
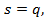
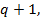вектор 
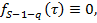при 
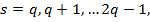вектор 
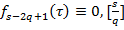селей час число 
.
Из системы (8) находим
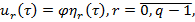(11)
где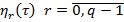 
— произвольные, отличные от нуля 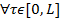неизвестные функции, определявшееся наследующем шаге, -собственные вектор матрицы 
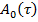соответствующие нулевому собственному значения.
Уравнение (9) с учетом (11) при r=0 имеет вид
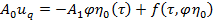. (12)
Для решения уравнения (12) необходимой достаточно, чтобы выполняли условия разрешимости
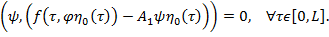
или
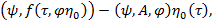(13)
где, 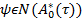элемент ноль-пространства сопряженной матрицы 
.
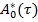Уравнения (13) запишем следующим виде
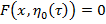(14)
Таким образом получаем относительно неизвестных функций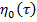 
неявный уравнений. Предположим, что для уравнений (14) выполняются все условия теоремы о неявной функций [2] и определим 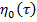. Условия (13) для уравнения (12) выполняются то находим
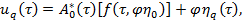(15)
где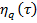 
— неизвестная функция, определяющаяся на следующем шаге, 
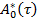— обобщенно-обратная матрица к матрицы 
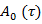имеет вид
.
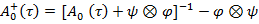— знак тензорный произведение.
С учетом (12) при р=1 из уравнения (10) когда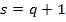 
получаем
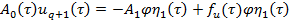. (16)
Условия разрешимость для уравнения (16) имеет вид
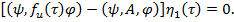(17)
Согласно условия теоремы 1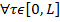 
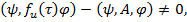
тогда из (17) определим
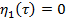(18)
Учитывая выполнение условия (17) из уравнения (16) находим
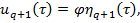(19)
где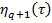 
— неизвестная функция определяются следующим шаге.
Продолжая процесс определений неизвестный коэффициенты ряда (6) уравнения (10) запишем
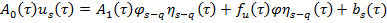, s=q+1, q+2,… (20)
Условия разрешимо с для уравнения (20) имеет следующем виде
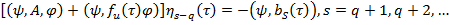(21)
Отсюда определим неизвестная функция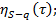 
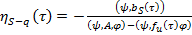. (22)
Тогда из уравнения (20) определяются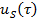 
вектор следующем образом
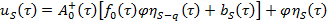, (23)
где неизвестная функция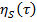 
определяются на следующем шаге. Описанная здесь схема решения показывает, как можно найти элементы формального разложения (6), т. е. векторы 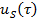c любом номером s=0,1,….
Теорема 1 доказана.
Теперь покажем, что формальные решение являются асимптотическим разложениям и некоторых точных решений системы (1). В связи с этим рассмотрение вводим так называемся m-тое приближение к искомым решением системы (1) в веди
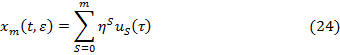
Пуст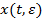 
приставляет собой точное решение системы (1), удовлетворяющее при 
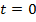тем же начальным условиям, что и 
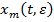. Тогда можно показать, что приближенное решение 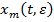асимптотически сходится к точному решению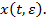 
Не останавливаясь подробно на деталях доказательства укажем основные его этапы. Наряду с системой (1) рассмотрим эквивалентную ей систему уравнений первого порядка
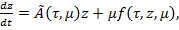(25)
в котором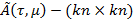 
-матрица и 
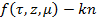-мерные вектор имеет структуру
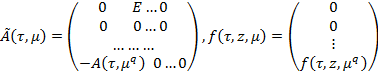
где 0-нулевая, E–единичная 
матрицы. Эта система получаются из системы (1) посредством замены
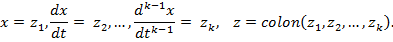
Для уравнения (25)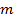 
— приближенный будет 
.
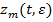Лемма. Пусть выполняются условия теорема 1, тогда 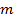— приближение 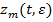удовлетворяет уравнению
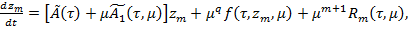(26)
где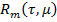 
— вектор-функция равно мерно ограниченная на сегменте [0,L]
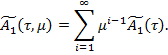
Доказательство леммы производится постановкой выражения
в уравнение (25) и последующей оценки полученных выражений (см [3]).
Введем рассмотрение разность
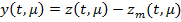. (28)
где 
и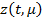 
— приближенные и точное решение системы (25), соотствуюшее одиноким начальным условиям. Очевидно, вектор-функция 
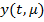удовлетворяет уравнению
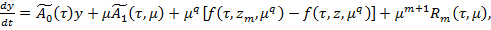(29)
с начальными условиями
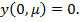(30)
Теорема 2. Предположим, что выполнении условия теоремы 1, и вектор-функция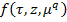 
удовлетворяет условию Лепщица с постоянной 
:
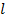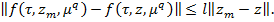(31)
Тогда найдется такие положительные числа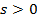 
и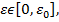 
что при 
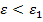на интервал 
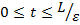будет выполняется неравенство:
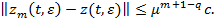(32)
Доказательство. Легко видеть, что система (29) с условиям (30) эквивалентна следующей системе интегральных уравнений:
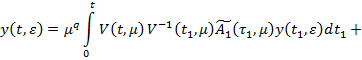
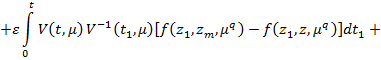
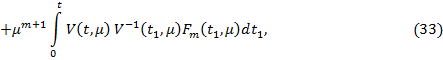
где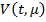 
являются решение задачи
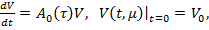(34)
удовлетворяющие условию
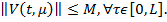(35)
Из (33), учитывая неравенство (31) и (35) получим
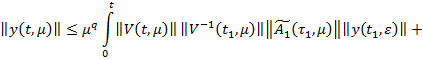
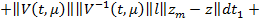
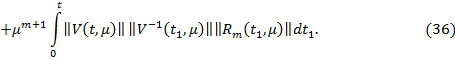
Согласно равномерно ограниченности на [0,L].
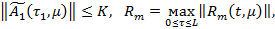
из неравенства (36) следует неравенство
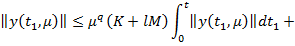
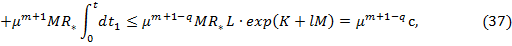
где
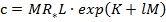
Тогда для системы (1) получаем оценку вида
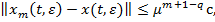
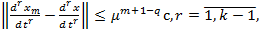(38)
Теорема 2 доказана.
Литература:
1. Алишев А. Г. Решение нелинейных дифференциальных уравнений дробного ранга. // ДАН. УССР, сер. А, Н6, — 1982, — с. 6–9.
2. Басилева А. Б., Бутузов В. Ф. Сингулярной возмущённые уравнение в критических случаях. — Изд. МГУ. — 1978. — 105 с.
3. Фихтенгольц Б. П. Основы математического анализа. — М.: Наука, — 1968, — 440 с.
4. Алишев А. Г. Приближенные решение системы нелинейных дифференциальных уравнений второго порядка. Препринт. АНУзССР, НПО «Кибернетика», Т. — 1994, — 59 с.
