Дано теоретическое обоснование увеличения коэффициента использования кислорода воздуха при биологической очистке сточных вод за счет организации нисходящего потока по периферии аэротнка. Показана конструкция вихревого эрлифтного устройства (ВЭУ), которое обеспечивает выгодный гидравлический режим работы сооружения биологической очистки. Приведена предлагаемая схема размещения ВЭУ в аэротенке.
Ключевые слова: сточные воды, биологическая очистка, аэротенк, система аэрации, вихревое эрлифтное устройство.
Практика эксплуатации современных сооружений аэробной биологической очистки сточных вод показывает, что себестоимость процесса очистки на 60–80 % зависит от эффективности применяемой системы аэрации, являющейся наиболее энергоемким элементом очистных сооружений. В связи с этим оптимизация процессов расчета и эксплуатации аэрационных систем является весьма актуальной задачей.
Скорость массопередачи кислорода, кг/с, из газовой фазы описывается уравнением [1]:
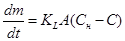 , (1)
, (1)
где KL — коэффициент массопередачи жидкой пленки, м/с;
А — площадь межфазового контакта, м2;
Сн — концентрация насыщения жидкости газом, кг/м3;
С — концентрация растворенного в жидкости газа, кг/м3.
Предполагается определять коэффициент массопередачи жидкой пленки по уравнению Хигби:
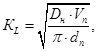 (2)
(2)
где DH — коэффициент нестационарной диффузии кислорода газа в жидкость, м2/с;
Vn — скорость всплывания пузырька воздуха, м/с;
dn — диаметр пузырька воздуха, м.
Формула Хигби описывает процесс нестационарной молекулярной диффузии через тонкую жидкостную пленку, часть поверхности которой движется вместе с набегающим на пузырек потоком жидкости. Описываемые формулой (2) процессы протекают при переходном режиме всплывания газового пузырька (переход от ламинарного режима к турбулентному). Нижняя граница переходного режима всплывания воздушного пузырька характеризуется следующими условиями: диаметр пузырька воздуха dп = 0,12·10-3 м; скорость всплывания пузырька воздуха Vп = 0,0082 м/с; критерий Рейнольдса Re = Vndn/v = 1, здесь ν — кинематический коэффициент вязкости, м2/с. Коэффициент гидравлического сопротивления при всплывании пузырька ζ= 24/Re = 24. Верхняя граница переходного режима всплывания воздушного пузырька характеризуется следующими условиями: dn = 0,83–10-3 м; Vn = 0,38 м/с; Re = 315; ζ =0,076.
Пневматические системы аэрации тонкодиспергированным воздухом позволяют получить пузырьки диаметром dn от 2,5·10-3 до 5·10-3 м, в связи с чем для описания процесса массопередачи этих систем более корректно использовать формулу Данквертса. Теория Данквертса описывает турбулентный режим массопередачи (dn > 0,83·10-3 м), при котором турбулентные вихри, зарождающиеся на поверхности пузырька воздуха, контактируют с ней в течение короткого промежутка времени, в результате чего происходит обновление поверхности границы раздела фаз.
В соответствии с теорией Данквертса:
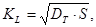 (3)
(3)
где DT — коэффициент турбулентной диффузии, м2/с;
S -фактор обновления границы раздела фаз, с-1.
В своих работах Данквертс не предлагает какого-либо конкретного подхода для определения величины S. Одна из попыток определения численного значения S, исходя из анализа баланса энергий (термодинамический подход), сделана в [2]. Было высказано предположение, что процесс обновления поверхности раздела под действием турбулентных вихрей должен быть связан с работой, совершаемой на границе раздела фаз. Поскольку работа, совершаемая при обновлении поверхности, обусловлена наличием поверхностного натяжения, величина новой поверхности, образующейся в единицу времени S, с-1, за счет турбулентного обмена элементов жидкости на единице поверхности, может быть определена как:
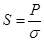 (4)
(4)
где Р = ζρVn3/2 — работа, совершаемая на единице поверхности в единицу времени, Вт/м2; σ — коэффициент поверхностного натяжения, Дж/м2.
Тогда
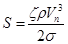 , (5)
, (5)
где ρ — плотность жидкости, кг/м3.
Поскольку S является величиной, обратной среднему значению времени экспозиции, и может быть интерпретирована как частота обновления поверхности, было предложено определять S не в виде отношения элементарной работы Р к коэффициенту поверхностного натяжения σ, а как отношение секундной работы, совершаемой силами гидродинамического сопротивления АT, Дж/с, к поверхностной энергии пузырька воздуха Е, Дж:
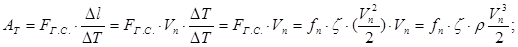 (6)
(6)
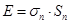 , (7)
, (7)
где FГ.С. = fпζpVn3/2 — сила гидродинамического сопротивления, Н;
Δl- расстояние, м, на которое перемещается пузырек воздуха за время ΔТ, с;
fп — площадь поперечного сечения пузырька воздуха, м2;
Sп — площадь поверхности пузырька воздуха, м2.
Тогда
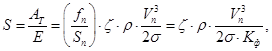 (8)
(8)
где Кф = Sп/fп — коэффициент формы пузырька воздуха.
Предложенное уравнение (8) для вычисления значения фактора обновления границы раздела фаз всплывающего пузырька воздуха отличается от формулы (5) лишь наличием дополнительного коэффициента Кф.
Введение коэффициента формы пузырька воздуха Кф учитывает специфику сил поверхностного натяжения FП.Н. и гидродинамического сопротивления FГ.С.. Силы гидродинамического сопротивления действуют на площадь поперечного сечения пузырька воздуха fп, а силы поверхностного натяжения — на поверхность раздела фаз пузырька воздуха Sп.
С учетом равенства (8) формула (1) примет вид:
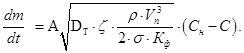 (9)
(9)
Интегрируя уравнение (9) в интервале переменных dm (от 0 до Δm) и dt (от 0 до ΔT), имеем:
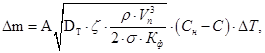 (10)
(10)
где Δm — масса растворившегося кислорода, кг;
ΔТ — время контакта воздуха с водой, с.
Для одиночного пузырька воздуха, имеющего площадь поверхности Sп и объем Wп, величина снижения концентрации кислорода ΔС, кг/м3, в газовой фазе будет описываться уравнением:
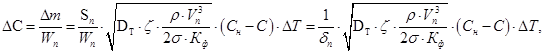 (11)
(11)
где δп = Wп/Sп — дисперсный размер пузырька воздуха, м.
Коэффициент использования кислорода воздуха КИ, определяемый как отношение снижения концентрации кислорода воздуха ΔС, растворенного в воде, к концентрации кислорода воздуха Ск.в, подаваемого в систему аэрации, может быть вычислен по формуле:
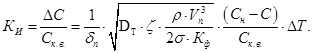 (12)
(12)
Время контакта воздуха с водой в случае всплывания одиночного пузырька со скоростью Vп в слое жидкости высотой Н определяется по соотношению ΔТ =H/Vп.
Время контакта ΔТ при одновременном всплывании группы пузырьков приближенно может быть вычислено по эмпирической зависимости:
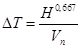 .
.
Тогда
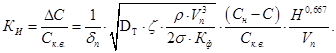 (13)
(13)
Зависимость (13) может быть использована для инженерных расчетов окислительной способности (ОС) пневматических систем аэрации с различной дисперсностью пузырьков воздуха:
ОC = KИCк.в.Qв, (14)
где Qв — расход воздуха, подаваемого в систему аэрации, м3/ч.
Повысить эффективность пневматической системы аэрации аэротенка, не увеличивая его глубину, возможно, организовав движение иловой смеси навстречу всплывающему пузырьку воздуха (принцип противотока). Как правило, противоток создается за счет выделения в аэрационном объеме аэротенка специальных эрлифтных зон, занимающих 0,15–0,25 площади аэротенка.
В эрлифтной зоне за счет эрлифтного эффекта создается восходящий поток иловой смеси. Иловая смесь поступает в верхнюю часть зоны аэрации и далее движется вниз навстречу всплывающим пузырькам воздуха, выходящим из пневматических аэраторов. В этом случае скорость движения пузырька относительно зеркала жидкости будет определяться как разность скорости свободного всплывания пузырька Vп и скорости нисходящего потока Vн, т. е. V= Vп — Vн.
Авторами была разработана конструкция вихревого эрлифтного устройства (ВЭУ), которое предлагается использовать в качестве дополнительного устройства для улучшения работы штатной мелкопузырчатой системой аэрации [3, 4]. Схема и общий вид (ВЭУ) представлены на рис.1.
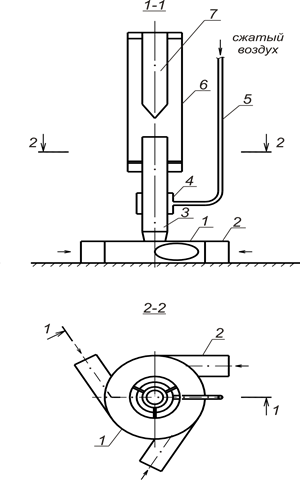
Рис. 1. Схема вихревого эрлифтного устройства (ВЭУ): 1- входная камера; 2-входной патрубок; 3- ствол устройства; 4- камера смешения; 5- воздушный патрубок; 6 — вихревая камера; 7 — тело обтекания
ВЭУ устанавливается по центру аэротенка в затопленном состоянии и за счёт поступления иловой смеси по тангенциально присоединенным к камере 1 патрубкам входа 2 создает в своем стволе 3 и вихревой камере 6 закрученный восходящий поток иловоздушной смеси. Тело обтекания 7 предназначено для лучшей диспергации пузырьков воздуха в вихревой камере 6.
Мелкодисперсные пневматические аэраторы (штатная система аэрации) устанавливаются вдоль бортов аэротенка. Над штатной системой аэрации за счет работы ВЭУ создается закрученный нисходящий поток иловой смеси, в результате чего реализуется принцип противоточной аэрации, который позволяет увеличить продолжительность контакта жидкости с воздухом благодаря снижению скорости подъема воздушных пузырьков, способствует более эффективному обновлению диффузионной поверхности границы раздела фаз газ-жидкость [2].
В стволе ВЭУ процесс массопередачи кислорода в жидкость также интенсифицируется за счет высокой турбулизации восходящего потока иловой смеси с воздухом, создаваемой радиальной составляющей вектора скорости.
Использование ВЭУ позволяет организовать более выгодный гидравлический режим в аэротенке без изменения его конструкции — режим ячеистого аэротенка.
В зоне действия каждого ВЭУ с шагом, равным ширине аэротенка создаётся гидравлическая ячейка, в которой внешний нисходящий закрученный поток иловой смеси реализует режим аэротенка-смесителя (рис. 2). Между собой отдельные ячейки соединяются по принципу аэротенка-вытеснителя, следовательно, создается гидравлический режим ячеистого аэротенка, позволяющий более плавно распределить нагрузку на активный ил по длине сооружения.
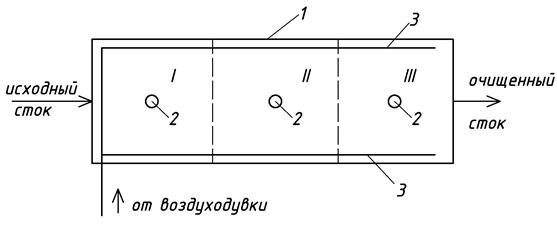
Рис. 2. Схема установки ВЭУ в аэротенке: 1 — аэротенк; 2 — ВЭУ; 3 - пористые трубы (система аэрации); I-III — гидравлические ячейки
Таким образом, дополнительное оснащение коридорных аэротенков-вытеснителей вихревыми эрлифтными перемешивающими устройствами позволяет существенно повысить массообменные характеристики системы аэрации и оптимизировать гидравлический режим аэротенка без изменения его конструкции.
Экспериментальные исследования показали, что использование ВЭУ в аэротенке позволило повысить эффективность пневматической системы аэрации в 1,4 раза, улучшить седиментационные свойства активного ила, существенно повысить эффективность биологической очистки сточных вод по взвешенным веществам, БПКполн, ХПК, аммонийному азоту и фосфатам.
Литература:
1. Мешенгиссер, Ю. М. Моделирование процесса массопередачи при аэрации воды [Текст] / Ю. М. Мешенгиссер, Ю. Г. Марченко// Водоснабжение и санитарная техника. — № 6. 2000. C. 20–21.
2. Брагинский, Л. Н. Моделирование аэрационных сооружений очистки сточных вод [Текст] / Л. Н. Брагинский, М. А. Евилевич, В. И. Бегачев — Л.: Химия, Ленингр. отд-ние, 1980. 143 с.
3. Андреев С. Ю. Интенсификация работы системы пневматической аэрации аэротенков с применением вихревых эрлифтных устройств [Текст] / С. Ю. Андреев, Б. М. Гришин, Н. Г. Вилкова, И. А. Гарькина, М. В. Бикунова// Водоочистка. — 2012. — № 5. С. 6–13.
4. Андреев, С. Ю. Высокоэффективные конструкции аэраторов пневматического типа для биологической очистки сточных вод [Текст]: депонированная рукопись № 1891-В2004 / С. Ю. Андреев, Б. М. Гришин, С. Н. Хазов, М. В. Бикунова, С. В. Максимова. — М.: ВИНИТИ, 2004. 120 с.







