Марковская игра «Большой матч» в классе стационарных стратегий

Марковская игра «Большой матч» (сокращенно БМ), как представитель марковской игры с конечным множеством состояний и конечными множествами решений игроков и критерием предельного среднего выигрыша первого игрока, изучена в работах [1–6]. В данной работе представлено очень простое доказательство решаемости БМ в классе стационарных стратегий в виде случайного механизма T(m; k).

1. Описание игры БМ. Игра БМ может быть представлена тремя формальными матрицами Г₁, Г₂ и Г₃ следующим образом:

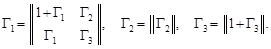
Формальная матрица Г_i (i = 1, 2, 3) представляет собой i-е состояние игры БМ. Процесс разыгрывания игры БМ состоит в следующем. На первом шаге в состоянии Г₁ игроки I и II независимо друг от друга выбирают строку i и столбца j соответственно. В результате складывается ситуация (i, j). После чего согласно элементу γ_ij формальной матрицы Г₁ определяется выигрыш игрока I и следующее состояние игры. Так, например, при ситуации (1, 1) γ₁₁ = 1 + Г₁ и игрок II платит игроку I единицу и следующим состоянием игры будет снова Г₁. Состояния Г₂ и Г₃ являются поглощающими, ибо, попадая в одно из них, игра останется в нем навсегда. На каждом шаге игры игроки оглашают свои решения с помощью монеты. Показ герба означает, что игрок I (II) выбрал первую строку (первый столбец), а показ решетки — вторую строку (второй столбец).

Введем обозначения: ξ_n (η_n) — решающая функция, представляющая собой вероятность выбора решения «герб» игроком I (II) на n-м шаге игры; π = (ξ₁, ξ₂, …, ξ_n, …) — стратегия игрока I; φ = (η₁, η₂, …, η_n, …) — стратегия игрока II; ξ^∞ = (ξ, ξ, …, ξ, …), η^∞ = (η, η, …, η, …) — стационарные стратегии игроков I и II, соответственно; 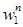(π, φ) — средний суммарный выигрыш игрока I за n шагов при стратегиях игроков π и φ и начальном состоянии Г₁; 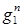(π, φ) = 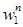(π, φ)/n — средний выигрыш игрока I за один шаг в n шаговом игре при π и φ и начальном состоянии Г₁. Стратегии игроков π^* и φ^* оптимальны, если справедливо двойное неравенство 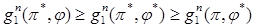для всех n ≥ 1 и произвольных π и φ. Оптимальные стратегии игроков π^* и φ^* и значение игры БМ с конечным числом шагов  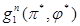могут быть определены методом динамического программирования [4, 5].

2. БМ в классе стационарных стратегий. Представим в явном виде целевую функцию 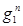(x^∞, h^∞). При решающих функциях ξ и η матрица вероятностей перехода за n шагов и вектор выигрышей имеют вид:

 

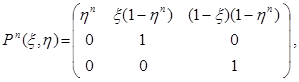
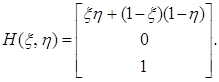
Отсюда следует, что

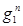(x^∞, h^∞) = σ_n [ξη + (1 — ξ)(1 — η)] + (1 — ξ)(1 — σ_n),

где σ_n = (1 + η + η² + … + η^{n — 1}) / n. Пусть σ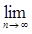_∞ =σ_n. Тогда, целевая функция g₁(x^¥, h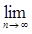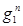^¥) = = (x^∞, h^∞) игры БМ с бесконечным числом шагов в классе стационарных стратегий имеет вид

g₁(x^¥, h^¥) = σ_∞ [xh + (1 — x)(1 — h)] + (1 — x)(1 — σ_∞).                                         (1)

Известно, что для любого заданного eÎ [0, 1] (см. [7, с. 50])

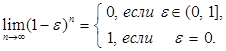
Следовательно, σ_∞ = 1 при h = 1 и σ_∞ = 0 при h = 1 — e, eÎ(0, 1]. Отсюда и из (1) следует, что

g₁(x^¥, h^¥) =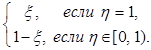

Теперь легко установить, что нижнее значение игры БМ в классе стационарных стратегий 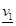 = ½, а верхнее значение игры  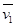= 1. Отсюда следует

Теорема Джиллетта. Игра «Большой матч» с бесконечным числом шагов в классе стационарных стратегий не имеет значения.

3. Событие с вероятностью ноль. Невозможное событие — событие, которое не может произойти в результате данного опыта. Ему приписывают вероятность 0. Ставим вопрос: из того, что вероятность события равна нулю, следует ли, что оно невозможное событие? Частота W_n(A) события A определяется, как отношение m/n, где m — число наступлений события А в n независимых испытаниях. Закон больших чисел в форме Я. Бернулли утверждает, что каково бы ни было e > 0, 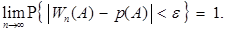 Согласно этому закону событие A имеет вероятность нуль не только в случае, когда его частота равна нулю, но и в случае, когда его частота является бесконечно малой величиной. Из того, что вероятность события A равна нулю, следует только, что при неограниченном повторении опыта оно будет появляться сколь угодно редко [14, c. 90–92].

Здесь нам остается констатировать, что в доказательстве теоремы Джиллетта не учтено то, что в бесконечных опытах событие с вероятностью 0 может произойти, а событие с вероятностью 1 — может не произойти. В этом доказательстве для игры БМ молча введено жесткое правило: если вероятность η = 1, то игрок II не имеет право показать «решетку».

При изучении игры БМ нельзя упускать из виду случай, когда вероятность выбора решения «герб» игроком II h = 1 — e и e ® 0, т. е. когда в соотношении (5) e является бесконечно малой величиной. Так, если в (5) положить ε = ln 2/ n, то получим

 

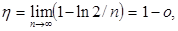
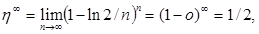
где o — бесконечно малая величина (обозначение И. Ньютона).

Отсюда следует, что σ_∞ = ½ и g₁(ξ^∞, η^∞) = ½ × x × 1 + (1 — x) × ½ = ½. Заметим, что данное равенство верно при любом значении xÎ [0, 1]. Это значит, что независимо от того, какую стационарную стратегию ξ^∞ применяет игрок I, при стационарной стратегии (1 — o)^∞ игрока II цена игры g₁ равна ½.

Для дальнейшего заметим, что в случае, когда e — вероятность перехода игры БМ из состояния Г₁ к одному из поглощающих состояний Г₂ или Г₃, является бесконечно малой величиной, целевая функция g₁(1^∞, η^∞) может принимать любое значение из интервала [0, 1]. Действительно, если положить e_n = l/n, где l произвольное положительное число, то

η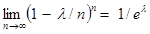^∞ = , σ_∞ = 1/e^l, и g₁(1^∞, η^∞) = 1/e^l.

4. Случайный механизм T(m, k). Рассмотрим урну T, содержащую бесконечное число сферических коробок. Каждая коробка содержит k (k ≥ 2) шаров. Во всех коробках, кроме одной, все шары белые. Одна коробка содержит k — 1 белых шаров и один черный шар. Игрок II вместо монеты Остапа Бендера может воспользоваться этой урной в качестве случайного механизма следующим образом. Он сначала из урны T наугад вынимает одну коробку, затем из нее вынимает m (m ≥ 1) шаров. Если все вынутые шары белые, то принимает решение Г, если среди них окажется черный шар, то принимает решение Р. После принятия решения, игрок II вложит все вынутые шары обратно в коробку, а коробку возвращает в урну T. Аналогично определяет игрок II свое решение на последующих шагах игры. Описанный случайный механизм выбора решения обозначим T(m, k). В случае, когда урна T содержит n сферических коробок, данный случайный механизм представим в виде T_n(m, k).

Вероятность появления черного шара в течение игры хотя бы один раз обозначим P(B).

Рассмотрим марковскую игру БМ с конечным числом шагов n, где игрок II свои решения принимает с помощью случайного механизма T_n(m, k). Поскольку урна T содержит n коробок и только в одной из них имеется черный шар, вероятность вынимания из нее коробки, содержащей черный шар, равна 1/n. Если вынута коробка с черным шаром, то вероятность вынимания из нее черного шара равна m/k. Согласно формуле полной вероятности вероятность появления черного шара в каждом опыте равна m/kn.

Вероятность непоявления черного шара в течение n-шаговой игры (тогда у игрока II получается цепочка решений ГГГ…Г_{(n букв)}) равна P(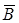) =  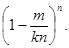При n → ∞ вероятность появления бесконечной цепочки решений ГГГ… у игрока II равна P() =

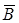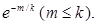
Таким образом, случайный механизм T(m, k) в игре БМ с бесконечным числом шагов порождает стационарную стратегию η^∞ игрока II такую, что вероятность появления решения Г (белого шара) на каждом шаге игры равна единице (1 — m/kn → 1, при n→∞), а вероятность появления этого же решения во всех шагах игры равна P() =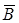

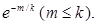
Теорема 1. В игре БМ для любого числа ε > 0 существует случайный механизм T(m, k), который порождает стационарную стратегию η^∞ игрока II такую, что | g₁(ξ^∞, η^∞) — ½ | < ε при любой стационарной стратегии ξ^∞ игрока I, где g₁(ξ^∞, η^∞) цена игры БМ.

Доказательство. При применении случайного механизма T(m, k) вероятность появления решения Г (белого шара) во всех шагах игры равна P(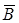) =  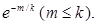Это значит, что в выражении (1) η^∞ = σ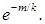_∞ =  Дробь m/k может быть выбрана так, что m/k » » ln2 с любой точностью. Тогда 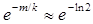= ½ и σ_∞ » ½. Поскольку когда σ_∞ = ½ цена игры g₁(ξ^∞, η^∞) = ½ при любом значении ξ, то для любого числа ε > 0 дробь m/k может быть выбрана так, что | g₁(ξ^∞, η^∞) — ½ | < ε. Теорема доказана.

Отметим, что если m = 693 и k = 1000, то e^–0,693 » 0,50007.

Следствие. В игре БМ с бесконечным числом шагов для игрока IIсуществует ε-оптимальная стационарная стратегия η^∞ такая, что при любой стационарной стратегии ξ^∞ игрока I цена игры удовлетворяет неравенство |g₁(ξ^∞, η^∞) — ½ | < ε для любого положительного числа ε.

Отсюда следует

Теорема 2. Марковская игра «Большой матч» с бесконечным числом шагов имеет значение, равное ½, а оба игрока — ε-оптимальные стационарные стратегии.

 

Литература:

 

1.         Gillette D. Stochastic games with zero stop probabilities // Contributions to the Theory of Games. V.III / Dresher M. Princeton, Univ. Press., 1957. Ann. Math. Studies № 39.

2.         Blackwell D. The big Matсh // STAM J. Appl / Math. 1970. № 19. Р. 473–476.

3.         Ибрагимов А. А. О марковской игре «большой матч» // РАН. Автоматика и телемеханика. 2000. № 11. С. 104–113.

4.         Ибрагимов А. А. Марковские игры с несколькими эргодическими классами // Украинский математический журнал. 2003. Т.55. № 6. С. 762–778.

5.         Ибрагимов А. А. Существование значения в общих марковских играх // Известия РАН. Теория и системы управления. 2004. № 2. С.5–15.

6.         Ибрагимов А. А. Оптимальные действия сторон в большом матче // VI Международная конференция MMR 2009 — Математические методы в теории надежности (Москва, 22–29 июня 2009 г.). Расширенные тезисы докладов. С. 256–260.

7.         Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т. 1. М.: Наука, 1970. 608 с.