Nowadays loosing layers of soil and making drainage peep-hole becoming important and actual problems in the agriculture of Uzbekistan. Because drainage-peep hole machines in soil layers and their scientific variants for local conditions were not come up with. For that age it is important to do scientific works in making drainage peep-hole. Soil layers especially in high salty lands and creating mathematical models of throwing sub-soil water.
In one size trend the pressure is P potential function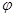 
(if it has) is the function of only one coordinate. The procedure of 2 part seeping liquid submits in the law of seeping lesson. This procedure simplified differential equation of action, in other words it makes possibility to express it.
Imagine, porous or full crack condition, changeable flowing pipe is given, its (flowing pipe) diagonal cut is DF and length is l, in this case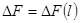 
will be (1-picture)
Imagine, if flowing pipe was filled by the same porous condition, in other words, pressure pipe has only unchangeable and only L coordinate. In this case a trend is depending on L coordinate and it come to the problem of one size trend. Trend’s constantly condition, flowing liquids in time units will be the same. Isobaric surface pressure unchangeable surface trend of liquid mass in time units is named mass quantity of surface and it marked with Q and in this liquid’s wasting mass or mass quantity (mass debit) flowing by M-isobaric surface. Using the law of the lesson we can take as a collection of liquid quantity flowing by pipe is equal with M in seeping condition.
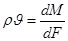, (1)
Using the law of the lesson speed module of seeping mass should be written as following
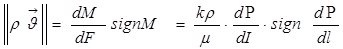. (2)
In this s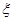 
g n M ва s 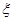g n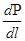 
formulations (2) determine the equation sign. Mathematic signum formulation is written as following.
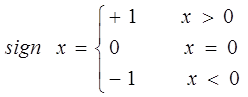
From above (4.24) formulation
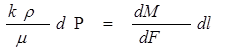(3)
This (3) formulation can be used for none compressed or less compressed liquids. For compressed liquid compactness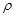 
and absolute stickiness pressure is changed in P. Changeable coefficient of the condition k or pressure with elastic feature of the condition depends on P. So in general pressure as length of the tend is changeable and it will be formulate with 
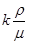pressure function
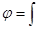
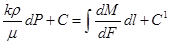(4)
In this 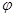- potential function; С and С1 — constant integral, (4) in formulation Р pressure express the connection between line l coordinate. Using above (3) formulation (4) we should write as following.
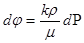(5)
Using founded formulas we write as following (5).
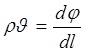(6)
With potential function for one size trend this equation can express seeping law equation in free liquid.
So, it can be learnt potential action of liquid in porous and crack condition on base of (6). So it can be conclude seeping mass speed is equal with gradient of potential function. These relations express general law of liquid mixture in potential action. We can count income flowing water mass if we equalize right
Keeping mass law for seeping trend. Keeping mass and weight law for seeping trend is written as [2]
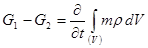(8)
Formula will be as following
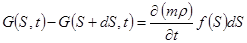
or
,
That’s to say we come to simple constantly equation.
If porous m depends on time, so
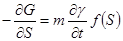(9)
Constant equation in coordinate formula will be as following
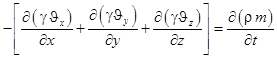
In this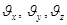 
-arrow projection of speed vector y, x, z will be equal in 
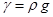тенг бўлади.
If we think sub soil water flows plainly, radically in the side of drainage-peep (crack), seeping moist water’s private property differential equation will be written as following
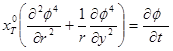, (10)
In this
.
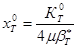We can write (18) equation as following.
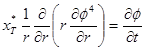. (11)
Action differential equations for nonpermanent seeping trend were recommended firstly by G.I Berenblatt, U. P. Jeltov and I. N. Konchina. We look through the solving when well stop working.
Imagine moist water filled crack by seeping on the side of crack and water distribute stationary pressure function till water stop flowing (for difermotianal layers)
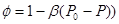, in this
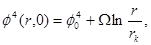(12)
In this: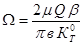 
.
Pressure spreading procedure is studied in two phase for solving matter. First phase moist water does not reach border of the crack. Second phase moist is the same with contour radius of crack. In the firs phase pressure spreading procedure in the border will be as following
,
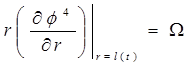or
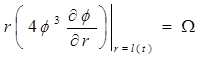(13)
If drainage –peep stops working, in this we can put following requirement in its wall
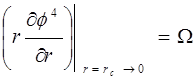
Solving matter is given in first part of this chapter private property differential equation should be contended.
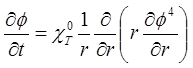(14)
If we do simple matters by using integral relations, the solution will be as following
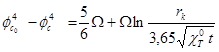(15)
After simple changing (15) we take following expression
,
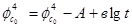In this
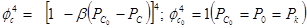(16)
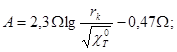
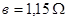(17)
Its graphic expresses line (lg t=0; t=1) crossing ordinate line.
А =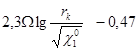 
(18)
This line is made by lg t corner tangent will be following:
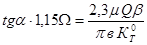(19)
If tg α answer is known,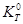 
may be found
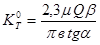(20)
It is to say that, equation given above should be solved with other way. So that we can look through solving plain matter of subsoil water trends in other works. After deserving farms fields in vegetation watered period, it determined that water dynamic was reached from 25–45 to 60–100 sm opening drainage-peep in some places in spring before salty washing period will bring lessening sub-soil waters and ripen crop fields in time. So it lessnes salt in soil content and it brings high harvesting of agricultural crops. On base on general information given from field researches and dynamic degree of sub-soil water and wetness of soil we can come on conclusion that it is very important growing crops before agro technique time and do planting works in time.
References:
1. Juraev F. U., Ubaydullayeva Sh.R. Filtration soli in the one-dimensional motion of the fluid and the potential energy in the mole drainage. European science review. 2014. Vinna 2014. № 7–8. 105–109 с.
2. А. П. Филин. Прикладная механики твердого деформируемого тела. М., «Наука», 1975 г. -832 с.
3. В. А. Мироненко Динамика подземных вод. М.,1983, 360с.
4. Ф. У. Жураев. Математическое моделирование напряженно-концентраци-онного состояния почвы. Наука и мир Международный научный журнал, г.Волгоград, № 1(5), 2014, 92–97 с.
