Развитие технологий защиты и передачи информации в настоящее время развивается весьма бурно, что стимулирует развитие криптографии, криптоанализа и других разделов информатики, обеспечивающих решение задач защиты информации. В статье рассмотрено построение полей GF(5) и GF(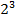
) по выбранному во множестве многочленов 
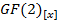. В поле GF(
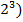построен конкретный пример, реализующий решение задачи открытого распределения ключей. Основными понятиями, используемыми в данной работе являются односторонняя функция секрета К, функция Эйлера, понятие поля. Целью данной статьи является изучение математического аппарата, который используется в процедуре открытого распределения ключей и составление модели, иллюстрирующей решение этой задачи с помощью изученного математического аппарата.
В настоящее время бурно развиваются технологии защиты и передачи информации. Это стимулирует развитие разделов математики, обеспечивающих решение задач защиты информации, таких, как: криптология (наука, состоящая из двух отраслей: криптографии и криптоанализа); криптография (наука о способах шифрования информации с целью ее защиты от незаконных пользователей); криптоанализ (наука о методах и способах вскрытия шифрования).
Соотношение криптографии и криптоанализа очевидно: криптография — защита, т. е. разработка шифров, а криптоанализ — нападение, т. е. атака на шифры. Эти две науки связаны друг с другом, и не бывает хороших криптографов, не владеющих методами криптоанализа. Дело в том, что стойкость разработанного шифра можно доказать только с помощью проведения различных атак на шифр, становясь мысленно в положение противника.
В работе мы опишем основные понятия «новой криптографии» и покажем, как в ней работает соответствующий математический аппарат.
Применение односторонней функции в криптографии позволяет:
- организовать обмен шифрованными сообщениями с использованием только открытых каналов связи, т. е. отказаться от секретных каналов для связи для предварительного обмена ключами;
- включить в задачу вскрытия шифра трудную математическую задачу и тем самым повысить обоснованность стойкости шифра;
- решать новые криптографические задачи, отличные от шифрования (шифровая подпись и др.)
Опишем идею в общем виде. Пользователь A, который хочет получать шифрованные сообщения, должен сначала выбрать какую-нибудь одностороннюю функцию Fk с секретом K. Он сообщает всем заинтересованным (например, публикует) описание функции Fk в качестве своего алгоритма шифрования. Но при этом значение секрета K он никому не сообщает и держит в секрете. Если теперь пользователь B хочет послать A защищаемую информацию x, то он вычисляет Fk(x) и посылает по открытому каналу к A. Поскольку A для своего секрета K умеет инвертировать Fk , то он вычисляет x по полученному значению Fk(x). Никто другой не знает K и поэтому в силу свойства односторонней функции с секретом не сможет за полиномиальное время по известному шифрованному сообщению Fk(x) вычислить защищаемую информацию x.
Таким образом, построена система передачи защищаемой информации, причем выполнены два новых свойства:
1) для передачи сообщений не требуется предварительный обмен ключами по секретному каналу связи;
2) стойкость шифра зависит от сложности решения трудной математической задачи инвертирования односторонней функции секретом.
Описанную систему называют криптосистемой с открытым ключом, поскольку алгоритм шифрования Fk является общедоступным или открытым.
Построение поля. Пусть множество GF(2) состоит из двух элементов 0 и 1, которые мы рассматриваем как остатки от деления на 2.
Введем на этом множестве операции сложения + и умножения *, которые есть, по сути, операции сложения и умножения остатков, поэтому определяется таблицами.
|
+ |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
|
* |
0 |
1 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
Аналогично можно рассмотреть остатки от деления на 4. Интересно заметить, что множество остатков от деления на 4 не является полем, так как для элемента 2 не существует обратного и вообще в этом множестве остатков, оказывается, есть делители нуля: 2×2=0. Для того чтобы множество остатков оказалось полем необходимо рассматривать остатки от деления на простое число. Например, остатки от деления на 5 образуют поле.
В криптографии, однако, используется поле GF(2) и уже с его помощью строятся другие важные поля GF(2n), для достаточно больших значений n. Покажем, как это делается.
Рассмотрим множество многочленов GF(2) [x], которое состоит из всех многочленов вида
*
+
*+…+
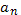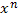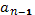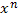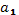*x+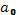
,
где аi ϵ GF(2)
Ясно, что аi =0 или аi =1. Выберем во множестве многочленов GF(2) [x] многочлен g=x3+x+1 и рассмотрим все остатки от деления на этот многочлен.
Обозначим множество остатков GF(23). Т. к. многочлен g(х) имеет степень 3, то все остатки от деления на него по теореме о делении с остатком, имеют степень не выше, чем 2. Таких остатков всего восемь:
GF(23) = {0, 1, х, х+1, х2, х2+1, х2+х, х2+х+1}.
Введем на этом множестве операции сложения и умножения по правилу сложения и умножения остатков.
Задача открытого распределения ключей. Опишем, как решается задача открытого распределения ключей в поле GF(23). Выберем в этом поле примитивный элемент р = р(х) = х и представим все ненулевые элементы поля в виде степеней этого элемента:
р = х
р2= х2
р3= х3= х+1
р4= х4= х2+х
р5= х5= х2+х+1
р6= х6= х2+1
р7=х7= 1.
В качестве односторонней функции выберем функцию F(x) = рх (mod g), где р — выбранный нами примитивный элемент, а g — многочлен g(x), выбранный нами для построения поля GF(23). Элементы р и g являются общедоступными.
Пусть два партнера А и В выбирают независимо друг от друга по одному натуральному числу а и b соответственно.. Каждый из участников держит эти числа в секрете. Затем каждый из них вычисляет новый элемент c и d по формулам:
c = рa(mod g), d = pb (mod g).
По открытому каналу связи партнеры обмениваются этими элементами, после чего партнер А. Зная свой секретный элемент a и полученный от В элемент d, партнер А вычисляет новый элемент
k = da = (pb)a = pab(mod g).
Аналогично поступает партнер В. Он вычисляет элемент
св = (ра)b = pab = k(mod g).
Теперь у партнеров А и В появился общий элемент поля k. Он и есть общий ключ для А и В. При формировании этого ключа использовались известные всем элементы p, g, ра, рb. Посторонние пользователи сети не знают только секретные элементы а и b. При этом каждый из партнеров в результате вычисляет новый, только им известный общий элемент поля k.
Например, пусть партнеры А и В каждый выбрали по натуральному числу а = 6 и b = 5.
Партнер А вычисляет с = р6 = х2+1, а партнер В вычисляет d = р5= x2+x+1. Эти элементы они пересылают друг другу, после чего партнер А получает:
k = da =(p5)6 = p30= (p7)4p2 = p2 = x2.
Точно также, партнер В при этом вычисляет cb= (p6)5 = p2= x2 = k.
Разумеется, на практике используются поля GF(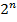
) при достаточно больших n, но в принципе задача решается так, как показано в примере.
Литература:
1. Бочкарева, О. В. Формирование профессиональных умений на занятиях по математике/ О. В. Бочкарева, О. В. Снежкина, М. А. Сироткина // Молодой ученый.- 2014.- № 2 (61).- С. 735–738.
2. Ладин, Р. А. Математика в учебном процессе строительного вуза / Р. А. Ладин, О. В. Снежкина, Г. А. Левова // Вестник магистратуры. -2013.- № 12–4 (27).- С. 56–59.
3. Бочкарева, О. В. Математические задачи как средство формирования профессиональных качеств личности / О. В. Бочкарева, Т. Ю. Новичкова, О. В. Снежкина, Р. А. Ладин // Современные проблемы науки и образования.–2014.–№ 2; URL: www.science-education.ru/116–12584
