Формирование структуры капитала компаний является одним из существенных аспектов деятельности финансового менеджмента организаций. Политика в области оптимизации структуры капитала влияет как на долгосрочную, так и на краткосрочную устойчивость компаний, позволяет ранжировать источники финансирования по их приоритетности и стоимости. Как следствие, в зависимости от приоритетности, выстраиваются отношения с поставщиками капитала. Чаще всего выделяются следующие поставщики капитала: акционеры и кредиторы. Первые направляют в компанию средства в виде собственного капитала, вторые — заемного, в виде кредитов и кредиторской задолженности. Политика в области формирования структуры капитала нацелена на поиск оптимального сочетания указанных источников финансирования, оптимальной пропорции между собственным и заемным капиталом.
Оценка стоимости собственного капитала предполагает расчет теоретической стоимости привлечения капитала потенциальных инвесторов с учетом страновых и отраслевых рисков. Для расчета обычно используются модели оценки финансовых активов, или CAPM-модели. Классическая модель CAPM имеет следующий вид:
Re = rf + β*(rm-rf),
где Re — ожидаемая ставка доходности на собственный капитал;
rf — безрисковая ставка доходности;
β — бета-коэффициент;
rm — ожидаемая доходность рыночного портфеля.
В современных прикладных расчетах используются несколько иные, более совершенные модели CAPM, которые содержат дополнительные параметры оценки рисков:
1. Модель спрэда риска дефолта [2];
2. Модель CAPM Goldman Sachs [3];
3. Модель суверенного риска дефолта, в которой все компании в стране одинаково подвержены воздействию суверенного риска;
4. Модель пропорционального риска дефолта, в которой степень подверженности суверенному риску пропорциональна степени воздействия на нее других видов рыночного риска, измеряемого при помощи бета-коэффициента.
Расчет доходности по 4-м указанным моделям оценки собственного капитала на основе ежеквартальных оценок для ОАО «Газпром» за период с 2006 по 2014 г. представим на сводном графике (рис. 1).
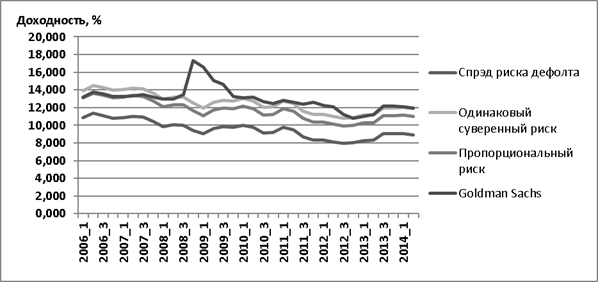
Рис. 1. Требуемая доходность по собственному капиталу, 4 модели оценки
Как видно из рис. 1, модели по уровню требуемой доходности собственного капитала располагаются в следующем порядке: модель спрэда риска дефолта, модель пропорционального риска, модель одинакового суверенного риска и модель CAPM Goldman Sachs. В целом требуемая доходность на собственный капитал относительно низка и за исследуемый период в среднем составляет от 9 до 12 % годовых. Кроме того, снижающиеся процентные ставки на американском долговом рынке, а также снижение российской страновой премии в целом привели к уменьшению требуемой доходности на капитал.
Оценка стоимости привлечения заемного капитала
Доходность по заемному капиталу является второй из ключевых компонент в оценке средневзвешенной стоимости капитала WACC и определяется следующим образом: к безрисковой ставке, которая представляет доходность десятилетних американских облигаций, добавляется страновой компонент риска, представленный спрэдом EMBI+Russia. Третьим немаловажным элементом является т. н. спрэд в зависимости от коэффициента покрытия, который рассчитывается как отношение нераспределенной прибыли к процентам по долговым обязательствам. Базовые значения спрэда представлены в книге А. Дамодарана [1, с. 300].
Именно оценка третьего элемента в модели является наиболее дискуссионным компонентом оценки стоимости заемного капитала. Если в случае с собственным капиталом все модели нацелены на использование бета-коэффициентов и представляют CAPM модели в той или иной форме, то в случае с заемным капиталом возможны различные варианты: в первом случае модель может быть представлена без изменений, т. е. третья компонента, надбавка в зависимости от коэффициента покрытия, добавляется к безрисковой доходности и страновой надбавке в виде спрэда EMBI+Russia. Во втором случае предпочтения инвесторов формируются следующим образом: третья компонента представляет собой произведение спрэда коэффициента покрытия процентов на рычаговой бета-коэффициент для собственного капитала в зависимости от долговой нагрузки, т. е. предпочтения кредиторов относительно испытываемого компанией риска повторяют ожидания акционеров и инвесторов. Именно второй вариант представляется наиболее правильным, для него далее произведены расчеты WACC.
Базовые коэффициенты покрытия процентов для ОАО «Газпром» представлены на рис. 2. Коэффициент рассчитывается на основе годовой отчетности и представляет отношение прибыли от продаж к процентам, уплаченным по заемному капиталу.
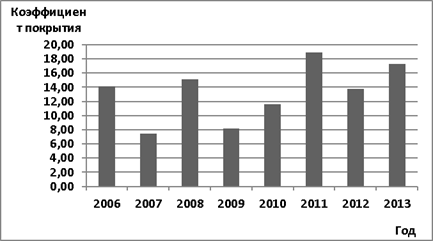
Рис. 2. Коэффициенты покрытия процентов ОАО «Газпром», 2006–2013 г.
Как видно из рис. 2, уровень коэффициента достигает максимума в 2011 г. за счет одновременного действия сразу двух факторов: во-первых, относительно более низкого уровня процентных расходов по долгу, которые не превысили 90 млрд. руб., во-вторых, высокого уровня прибыли от продаж (1 656 млрд. руб.). С другой стороны, рост стоимости заемных источников, падение прибыли от продаж привели к негативному воздействию на показатель в 2008–2009 гг., который, тем не менее, имеет тенденцию к росту в последние годы.
Помимо коэффициента покрытия еще одним показателем является стоимость фондирования заемным капиталом. Здесь представляется интересным сравнить две стоимости: с одной стороны, расчетную теоретическую стоимость заемного капитала, трехкомпонентная техника построения которой рассмотрена выше, и, с другой стороны, реальную стоимость привлечения долга. Вторая величина рассчитывается как отношение уплаченных процентов (стр. «Капитализированные проценты» и «Уплаченные проценты» ОДДС Консолидированной ежегодной отчетности ОАО «Газпром») к среднегодовому значению долга на основе ежеквартальной отчетности (к процентному долгу относится сумма значений в балансе по статьям «Краткосрочные заемные средства и текущая часть обязательств по долгосрочным займам» и «Долгосрочные займы»). Представим сравнение полученных значений на рис. 3.
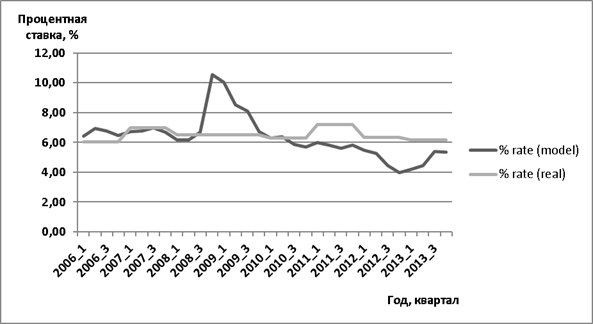
Рис. 3. Теоретическая и реальная стоимость заемного капитала ОАО «Газпром», 2006–2013 г.
Как мы видим, сравнение ставок показывает интересные особенности, присущие долговому рынку. Возможно выделить три участка на графике: на первом расчетная и реальная процентные ставки совпадают (2007 г.), на втором реальная процентная ставка ниже теоретической (2009 гг.), что, по всей видимости, на тот момент вызвано зафиксированной стоимостью обязательств, на третьем реальная ставка кредитования выше расчетной (2012–2013 гг.). Как мы видим, подобные «несовершенства» в течение макроэкономических циклов позволяют экономить денежные средства на процентах, привлекая долг перед кризисом и, напротив, снижать его во время спадов экономики.
Показав теоретическую и реальную процентные ставки по заемному капиталу, начнем менять фиксированные параметры на переменные, в зависимости от теоретического уровня долговой нагрузки, который меняется от 0 до 90 % капитала (активов) компании. При этом процентная ставка по долговым обязательствам США (безрисковая ставка), а также суверенный спрэд EMBI+Russia представляют в расчете константу, а меняется третий параметр, дополнительная рисковая надбавка в зависимости от коэффициента покрытия процентов с учетом изменения требований кредиторов аналогично предпочтениям акционеров (включение в расчет бета-коэффициентов). Представим трехмерную модель для заемного капитала на рис. 4.
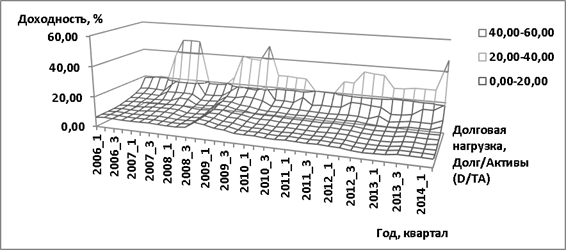
Рис. 4. Трехмерная модель доходности по заемному капиталу, ОАО «Газпром», 2006–2014 г.
Расчет средневзвешенной стоимости капитала (WACC)
Средневзвешенная стоимость капитала представляет взвешенную по долям капитала стоимость привлечения средств, которая учитывает как заемные, так и собственные средства компании. При учете стоимости заемного капитала следует иметь в виду то, что проценты по заемным средствам следует скорректировать на т. н. «налоговый щит», т. е. реальная стоимость привлечения капитала с учетом того, что проценты по заемному капиталу подлежат учету в расходах при расчете налога на прибыль, становится меньше на 20 %. Таким образом, представим формулу WACC для расчетов:
WACC = Re*de + Rd*dd*(1-t)
где Re — требуемая доходность по собственному капиталу;
de — доля собственного капитала;
Rd — требуемая доходность по заемному капиталу;
dd — доля заемного капитала;
t — ставка налога на прибыль.
Осуществим расчет средневзвешенной стоимости капитала для 4 кв. 2013 г. по модели собственного капитала CAPM Goldman Sachs и долговой нагрузке 50 % (соотношение Debt/Total assets (D/TA) — 50 %):
WACC = 18,175*0,5+7,501*0,5*(1–0,2) = 12,088 %
Рассчитанное значение показывает средневзвешенную стоимость капитала в одной конкретной точке пространства, т. е. для 4 кв. 2013 г. (конкретный момент времени) и определенной долговой нагрузки (50 %, конкретное значение левериджа). Построим на рис. 5 итоговую плоскость для WACC, в которой меняется как координата времени (с 1 кв. 2006 г. по 2 кв. 2014 г. включительно с шагом в 1 квартал), так и леверидж компании (от долговой нагрузки, равной нулю, до уровня D/TA в 90 %).
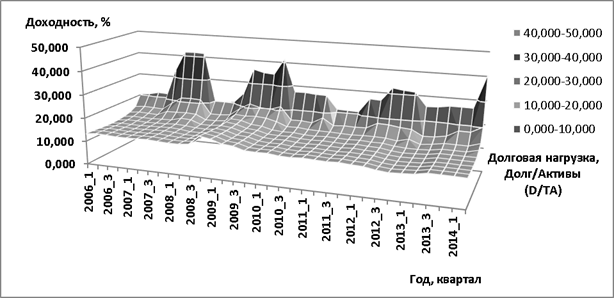
Рис. 5. Средневзвешенная стоимость капитала WACC, ОАО «Газпром», 2006–2013 г.
Для WACC на рис. 5 характерны следующие особенности: во-первых, вполне очевидно, что средневзвешенная доходность по капиталу меняется как в зависимости от координаты времени, так и от левериджа. Подверженность макроэкономическим циклам приводит к тому, что в моменты кризисов (на рис. 2008–2009 гг.) требуемая доходность по капиталу возрастает, в моменты роста экономики — несколько снижается. Во-вторых, применение формулы Хамады при оценке собственного капитала приводит к повышению общей требуемой доходности для WACC в зависимости от левериджа компании, т. е. чем выше долговая нагрузка, тем больше требования акционеров и кредиторов к генерируемой доходности по капиталу. В-третьих, во все временные интервалы наблюдается характерный минимум WACC, т. е. оптимальное значение левериджа, при котором средневзвешенная стоимость капитала минимальна. В-четвертых, указанный минимум все время меняется в зависимости от макроэкономической ситуации. Обозначим гипотезу, согласно которой компания может нести большую долговую нагрузку в моменты макроэкономических подъемов, при этом выгоды от применения левериджа на данных стадиях макроэкономического цикла выше, и проверим ее на практике: на рис. 6 показана ежеквартальная оптимальная долговая нагрузка компании ОАО «Газпром» согласно построенным четырем моделям стоимости собственного капитала.
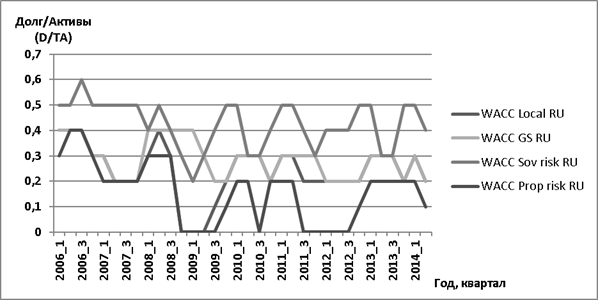
Рис. 6. Оптимальная структура капитала компаний, ОАО «Газпром», 2006–2014 гг.
Как мы видим на рис. 6, оптимальный леверидж компании увеличивается на «сырьевом пике» цен 2006–2008 г., достигая значений в 0,4–0,5 от всего капитала, т. е. долговая нагрузка в 40–50 %, созданная, например, за счет краткосрочных кредитов, вполне «безболезненно» могла быть воспроизведена руководством ОАО «Газпром». Кроме того, обращает на себя внимание тот факт, что модели WACC, созданные на основе различных моделей построения доходности по собственному капиталу, по-разному реагируют на изменение финансовых параметров деятельности компании, а также макроэкономическую конъюнктуру: наиболее стабильной является модель на основе модели CAPM Goldman Sachs, тем самым, несмотря на наиболее сложную методику построения, доказывая свое превосходство над другими моделями.
Рассчитав оптимальную структуру капитала для каждого момента времени (т. е. квартала), перейдем к оценке отклонений реально наблюдаемого левериджа от оптимального, минимизирующего средневзвешенное значение стоимости капитала WACC. При этом условно для текущей структуры капитала были установлены границы, в которые «попадает» текущее значение левериджа, с шагом (-0,05;+0,05). Например, если текущий леверидж составляет значение 0,223, то условно он относится к интервалу (0,15;0,25) и т. д. Представим оценку отклонений на рис. 7.
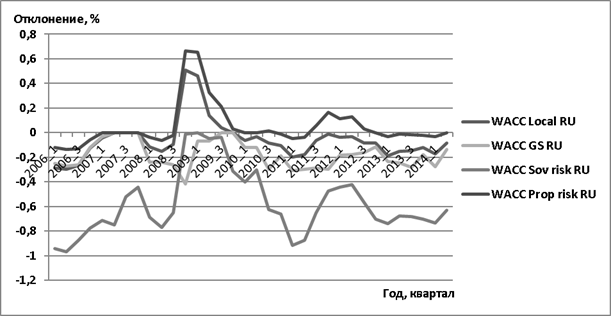
Рис. 7. Отклонения текущей структуры капитала от оптимальной (0), % выражение, 4 модели оценки собственного капитала
Интересным представляется проанализировать данные, представленные на рис. 7. Как мы видим, по трем моделям оценки собственного капитала (локальной, пропорционального риска и CAPM GS) получено примерно одинаковое движение динамики потерь от применения неоптимального левериджа. 2007 г. характеризуется соответствием текущей долговой нагрузки оптимальной, начиная с 2009 г. начинает усиливаться дисбаланс в пользу избыточного финансового рычага, максимальные потери по ряду моделей достигают ~0,4–0,6 %. Начиная с 2010 г. все модели действуют согласованно, за исключением модели суверенного риска. Таким образом, на наш взгляд, модель суверенного риска наиболее неочевидно передает экономическую действительность, а выбор следует снова остановить на CAPM GS.
Литература:
1. Дамодаран А. Инвестиционная оценка: инструменты и методы оценки любых активов / А. Дамодаран. — М: ЗАО «Бизнеском», 2011.
2. Лузан А. А. Методика обоснования рыночной премии за риск [Электронный ресурс] / А. А. Лузан — Электрон. дан. — Информационный интернет — портал flatik.ru. — Режим доступа: http://flatik.ru/metodika-obosnovaniya-rinochnoj-premii-za-risk (дата обращения 10.01.2015)
3. Рачков И. В. Расчет стоимости акционерного капитала с помощью модели Goldman Sachs [Электронный ресурс] / И. В. Рачков //Информационный интернет — портал cfin.ru. — Режим доступа: http://www.cfin.ru/finanalysis/value/goldman.shtml (дата обращения 10.01.2015)







