Приведен алгоритм синтеза дискретных управляющих воздействий, обеспечивающих минимум функционала качества процесса управления динамическими объектами. Алгоритм основан на применении теоремы об n-интервалах и использовании прогнозируемых значений управляемого процесса в рассматриваемом интервале времени. Для определения прогнозируемых значений выходных переменных использована дискретная передаточная функция объекта.
Ключевые слова: алгоритм, синтез, управляющих воздействий, дискретная передаточная функция, прогнозирование.
The algorithm is given. synthesis of discrete managing directors of the influences providing a minimum of functionality of quality of process of management of dynamic objects. The algorithm is based on applications of the theorem of n-intervals and use of the predicted values of the operated process in the considered time interval. For determination of the predicted values of output variables discrete transfer function of object is used.
Keywords:algorithm, synthesis, the operating influences, discrete transfer function, forecasting.
При создании систем управления технологическими процессами динамическими объектами необходимо использовать весь арсенал современной теории и практики автоматического контроля и управления и кроме того, необходимо иметь информацию о поведении технологического объекта управления под влиянием управляющих воздействий [1,2]. Эффективное управление процессами и промышленными объектами возможно в том случае, когда основные характерные черты, присущие объекту, представлены в виде математического описания.
Разработка оптимальных системах управления, способных обеспечить требуемое качество управления в условиях быстрых изменений параметров объекта при изменении показателей внешней среды, является актуальной научно-технической задачей. Решение поставленной задачи позволит существенно улучшить качество управления технологическими параметрами процесса.
В работе описывается алгоритм оптимальная управления, ориентированный на синтез дискретных управляющих воздействий, модулированных по амплитуде, и позволяющий рассчитывать значения управляющих импульсов с постоянным периодом, переводящих объект управления в новое, требуемое установившееся состояние и обеспечивающий стабильное и устойчивое нахождение объекта в его окрестности.
В основу базового алгоритма синтеза [3,4], положено то, что по истечении необходимого числа тактов управления NU, состояние объекта должно удовлетворять условиям:
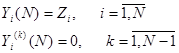(1)
Здесь N — количество выходных переменных объекта управления;
Yi(N) — значения i-ой выходной переменной по окончанию N –го такта;
Yi(k)(N) — значение k-ой производной i-ой выходной переменной;
Zi — требуемое значение (уставка) i-ой выходной переменной.
В отличие от базового в предлагаемом алгоритме оптимального управления математическая постановка задачи управления имеет следующий вид:
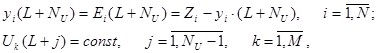(2)
где: L — текущий момент времени (такт квантования); М — число входных управляющих воздействий;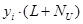 
— прогнозируемое значение i–ой выходной переменной на NU тактов вперед от текущего момента времени, 
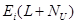— сигнал ошибки.
Анализ условий (2) позволяет сделать вывод о том, что при реализации данного алгоритма система управления не стремится к тому, чтобы объект управления по истечении выбранного числа тактов управления NU перевелся в новое установившееся состояние, характеризующееся постоянными и неизменными значениями выходных переменных. Алгоритм позволяет лишь рассчитывать значения управляющих воздействий, исходя из условия равенства выходных переменных по истечении NU тактов управления их требуемым значениям [3]. При этом в текущем такте квантования предполагается, что значения управляющих воздействий в течение последующего интервала управления меняться не будут. На самом деле, в каждом новом такте осуществляется пересчет значений управляющих воздействий по каждой входной переменной. Такой подход обеспечивает устойчивое, асимптотическое движение объекта управления к новому установившемуся состоянию и стабильное нахождение переменных, характеризующих его поведение в заданном диапазоне регулирования. Такое плавное изменение выходных переменных осуществляется вследствие того, что в каждом последующем такте амплитуда изменения управляющих импульсов при условии неизменности требуемых значений (уставок) и незначительных колебаний условий функционирования меняется на относительно малую величину, не вызывающую резких движений объекта и системы управления.
В условии (2) для определения значений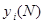 
можно использовать выражение:
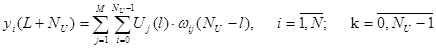(3)
Здесь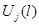 
— искомое значение j–го управляющего воздействия в l–ом такте; 
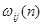— значение весовой функции канала j–й вход i–й выход в n–ом такте.
Причем весовая функция определяется как реакция на единичный импульс длительностью, равной величине такта квантования:
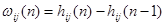, (4)
где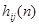 
— значение переходной функции канала j–й входа i-й выхода в n–м такте квантования.
Нахождению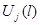 
, 
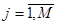должно предшествовать определение прогнозируемых значений вектора ошибки 
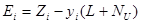в соответствии с фактическим состоянием объекта управления. Это обусловлено тем, что фактическое состояние объекта управления в силу неточности математической модели, ошибок в реализации рассчитанных управляющих воздействий, наличия различных возмущающих факторов, действующих на реальный объект, практически никогда не совпадает с состоянием, рассчитанным только по модели.
Для определения прогнозируемых значений ошибок, или, что тоже самое, прогнозируемых значений выходных переменных предлагается подход, основанный на использовании дискретных передаточных функций объекта управления [3]. Обозначим через:
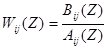(5)
дискретную передаточную функцию канала i–го выхода j–го входа, где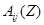 
и 
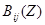— полиномы по степеням соответственно степене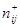й 
и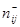 
. Тогда Z–преобразование выходной переменной можно представить в виде:
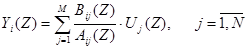(6)
Приведя правую часть выражения (6) к общему знаменателю, получим:
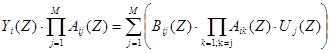(7)
Или в другом виде:
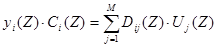(8)
где
, 
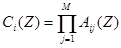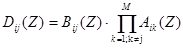(9)
Разделив левую и правую части (8) на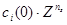 
получим:
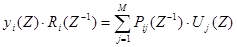(10)
где 
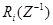и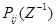 
— полиномы по обратным степеням оператора Z вида:
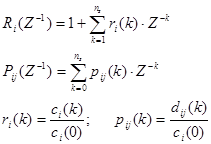(11)
На основе выражения (10) с учетом (11) легко получается рекуррентная формула для прогнозирования выходных значений объекта управления:
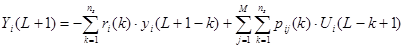(12)
Здесь ns — суммарный порядок передаточных функций, связанных с i–ой выходной переменной.
Для определения значения выходных переменных будем использовать выражение:
,
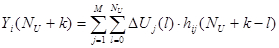где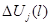 
— приращение j-го входного управляющего воздействия в l-м такте относительно его полного значения в (l-1)-м такте, т. е. 
.
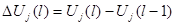При этом полное значение управляющего воздействия
,
,
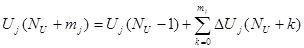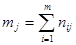автоматически получается равным величине, обеспечивающей требуемое установившееся состояния объекта управления.
Таким образом, полученный алгоритм управления динамическим объектом позволяет обеспечить перевода и удержание объекта на заданном значение за минимально возможное время и выбирать рациональные режимы работы агрегатов при оптимальном управлении всего процесса, что повысить производительность производства за счет минимизации длительности переходного процесса.
Литература:
1. Рей У. Методы управления технологическими процессами. -М: Мир, 1983. -368с.
2. Методы классической и современной теории автоматического управления / Под ред. К. А. Пупкова. ТОМ 1–4. — М.: МГТУим. Баумана, 2004г. –стр. 123.
3. Изерман Р. Цифровые системы управления. — М.: Мир, 1984.-стр 110.
4. Игамбердиев Х. З., Сиддиков И.Х Салахутдинов Р. Т. Двухуровневая схема синтеза воздействий для многомерных систем. // Межвузовский сборник научных трудов «Актуальные вопросы в области технических и фундаментальных наук». Выпуск 4. Ташкент: ТашГТУ. 2000.- стр. 38–40.
