Статья посвящена расчёту на прочность плоской статически неопределимой кольцевой рамы парусного свода покрытия мансардного этажа административного здания. Описывается разработанный алгоритм решения задачи с использованием программирования в САПР MathCAD.
Ключевые слова: статически неопределимая кольцевая рама, метод сил, эпюры изгибающих моментов, единичное и грузовое состояния, условие прочности, система автоматизированного проектирования MathCAD, программный модуль.
Анализ работы строительных конструкций показывает, что аварии возникают в результате случайного совпадения нескольких факторов: отклонения нагрузки в худшую сторону; снижения механических свойств материала; неблагоприятных условий эксплуатации; неточности расчётной схемы и т. д. Ведущие советские специалисты Н. С. Стрелецкий, А. А. Гвоздев, С. С. Давыдов и др. на основе глубоких обобщений, сделанных в различных областях строительных конструкций, разработали метод расчёта строительных конструкций по предельным состояниям. Этот метод в 1955 г. был принят в строительных нормах и правилах, а в 1971–1976 гг. значительно усовершенствован. Принципы расчёта по предельным состояниям позже нашли отражение в нормативной документации многих зарубежных стран. Предельным состоянием — состояние конструкции, при котором она перестает удовлетворять заданным требованиям эксплуатации или изготовления. Действующий СНиП предусматривает две группы предельных состояний: 1-я — по потере несущей способности или непригодности к эксплуатации; 2-я — по непригодности к нормальной эксплуатации [1,2].
Широкое распространение в строительных сооружениях находят стержневые конструкции в виде плоских рам, элементы которых работают в основном на изгиб [2,3]. Объектом исследования в данной работе является плоская статически неопределимая кольцевая рама (рис.1,b) парусного свода покрытия мансардного этажа административного здания (рис.1,а), состоящая из двух жёстко скреплённых между собой стержней из швеллера. Решение задачи проводим с применением системы автоматизированного проектирования MathCAD [4,5]. Исходные данные формируются следующим образом:
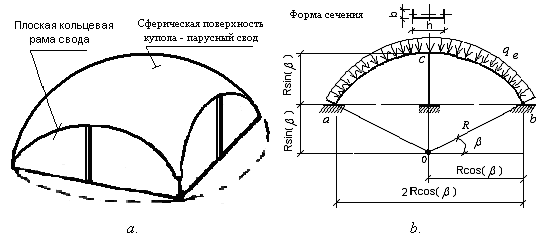
Рис.1. а) Схема парусного свода; b) Расчётная схема рамы свода
единицы измерения: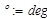 
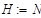
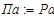
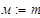
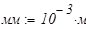
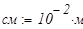
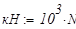
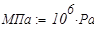
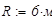
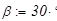. Нормативная нагрузка 
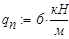— (снеговая нагрузка и собственный вес железобетона конструкции). Материал рамы — Сталь С255. Коэффициент надёжности по нагрузке 
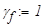— расчёт ведём по 2-й группе предельных состояний, 
, 
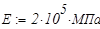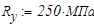— расчётное сопротивление стали изгибу по пределу текучести, по СНиП II-23–81. Расчётная нагрузка представлена как круговая равномерно распределённая по дуге окружности 
.
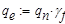Эквивалентная система показана на рис.2. За неизвестные при решении задачи методом сил приняты изгибающий момент Х1 в сечениях a и b, и нормальная сила Х2 в сечении с.
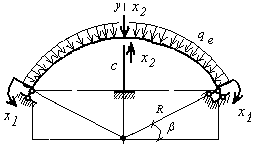
Рис.2. Эквивалентная система
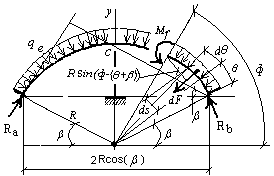
Рис.3. Грузовое состояние рамы
Система канонических уравнений метода сил имеет вид [2]
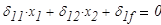
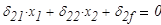
Грузовое состояние рамы представлено на рис.3. Элемент длины рамы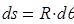 
воспринимает элементарную силу 
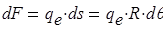. Из полученного уравнения равновесия 
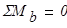определяем опорные реакции в символьной форме:
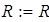
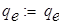
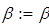
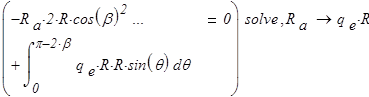
откуда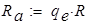 
ввиду симметрии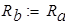 
Проверка правильности решения уравнения при помощи уравнения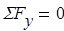 
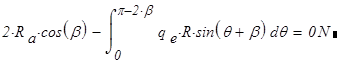
Изгибающий момент в кольце от заданной нагрузки (рис.3):
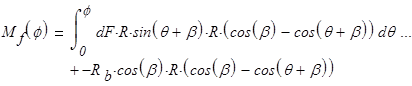
После подстановки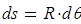 
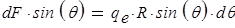составляем программный модуль для определения 
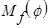по всей длине дуги:
Программный модуль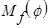
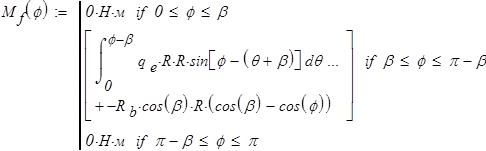
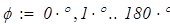
Эпюра изгибающих моментов 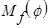представлена на рис.4 в полярной и декартовой системах координат:
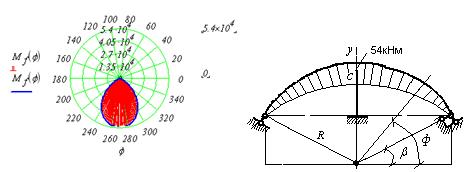
Рис.4. Эпюра изгибающих моментов 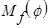в полярной и в декартовой системах координат
Определяем единичные изгибающие моменты в раме при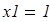 
(рис.5) и строим для проверки правильности аналитических выражений эпюры изгибающих моментов 
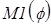в полярной и декартовой системах координат (рис.6).
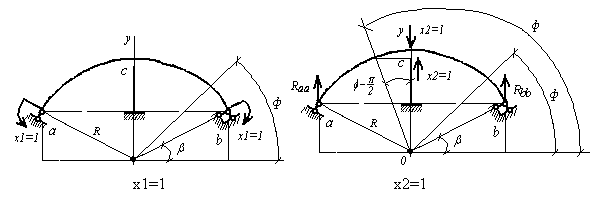
Рис.5. Единичные состояния рамы пр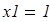и и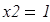 
Программный модуль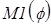
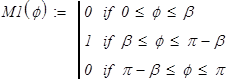
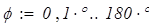
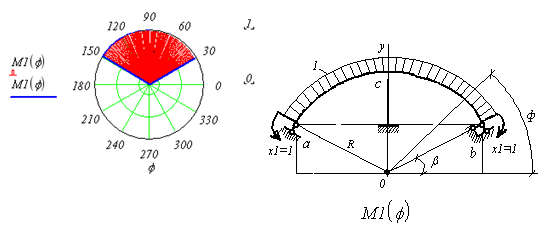
Рис.6. Эпюра изгибающих моментов 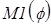в полярной и в декартовой системах координат
Рассмотрим единичное состояние рамы при 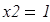(рис.5). Определяем опорные реакции из уравнения равновесия 
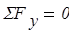в символьной форме:
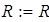
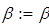
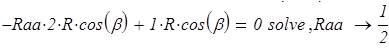
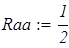
ввиду симметрии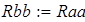 
. Проверка правильности решения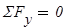 
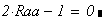. Строим эпюры 
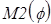(рис.7) при помощи программного модуля
Программный модуль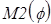
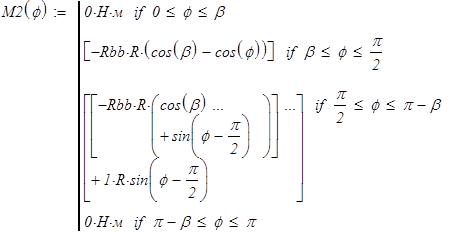
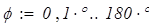
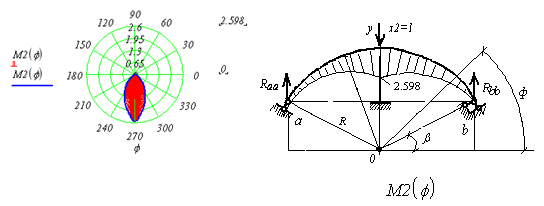
Рис.7. Эпюры изгибающих моментов 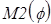в полярной и в декартовой системах координат
Рама парусного свода изготовлена из швеллера, номер которого определяем методом последовательного приближения. В начальном приближении примем № 20. Это необходимо для построения суммарной эпюры изгибающих моментов, по которой находится положение опасного сечения рамы и для этого сечения составляется условие прочности, откуда находится номер швеллера. Геометрические характеристики поперечного сечения швеллера:
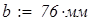
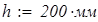
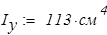
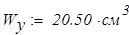
Определяем коэффициенты канонических уравнений:
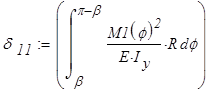
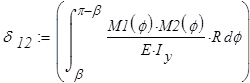
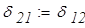
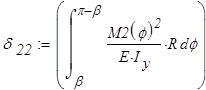
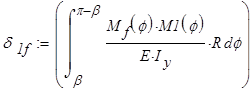
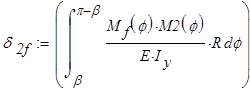
Канонические уравнения решаем в вычислительном блоке Given — Find
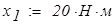
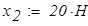
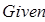
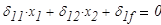
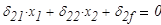
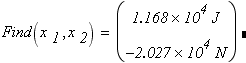
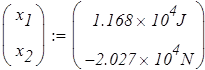
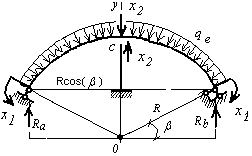
Рис.8. К определению опорных реакций в эквивалентной системе
Уравнение равновесия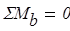 
для опорной реакции эквивалентной системы (рис.8) решаем в символьной форме: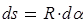 
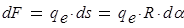
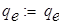
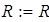
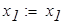
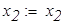
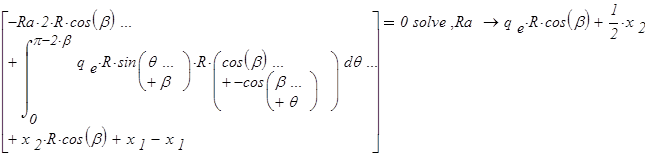
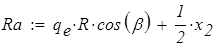ввиду симметрии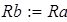 
Проверка правильности определения опорных реакций
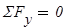
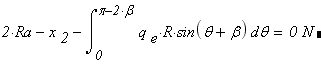
Построение суммарной эпюры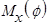 
в заданной раме. Отсечённые по участкам части рамы представлены на рис.9, а уравнения равновесия вставлены в программный модуль .
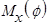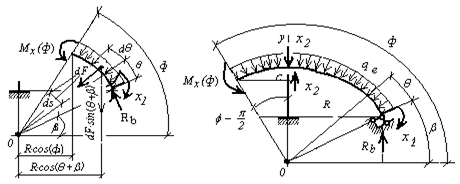
Рис.9. К определению изгибающих моментов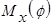 
по участкам заданной рамы (отсечённые части рамы)
Программный модуль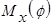
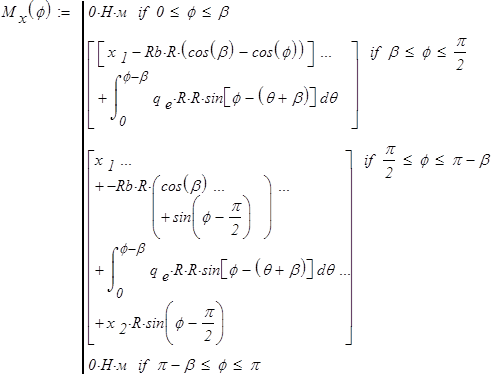
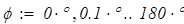
где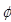 
— центральный угол. Эпюры 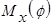показаны на рис.10.
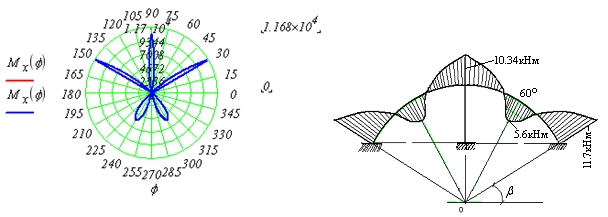
Рис.10. Суммарная эпюра изгибающих моментов 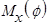в полярной и декартовой системах координат
Из условия прочности по нормальным напряжениям
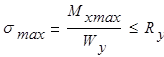
оставив один знак равно, вычисляем максимальное значение момента изгибающего
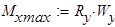
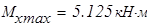
Максимальное значение момента изгибающего при заданной нагрузке равен
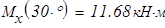
Из условия прочности при найденном значении изгибающего момента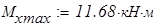 
находим момент сопротивления сечения
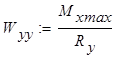
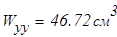
что соответствует швеллеру № 27.
Заключение. Задачи прочности элементов конструкций можно решать многими способами: вручную, с помощью стандартных программных средств (Excel, Ansys и т. д.). В данной статье рассмотрены возможности системы автоматизированного проектирования MathCAD в области математического моделирования при расчёте на прочность и жёсткость элементов конструкций и при этом эта система отличается от других большой наглядностью и ясностью при анализе решаемой задачи. Практическая ценность данной работы заключается в том, что алгоритм и методы решения в среде MathCAD задач прочности могут быть использованы в ВУЗах, так и при решении реальных технических задач [6,7].
Литература:
1. Ржаницын, А. Р. Строительная механика.-М.: Высшая школа, 1982. — 400 с.
2. Смирнов, А. Ф. Сопротивление материалов. — М.: Высшая школа, 1975. — 480 с.
3. Семёнов, В. В. Сопротивление материалов. Учеб. пособие. — Иркутск: Изд-во Иркут. гос. техн. ун-та, 2003. — 125 с.
4. Очков, В. Ф. Mathcad 12 для студентов и инженеров. — СПб.: БХВ — Петербург, 2005. — 464 с.
5. Кирьянов, Д. В. Самоучитель Mathcad 13. — СПб.: БХВ — Петербург, 2006. — 528 с.
6. Вафин, Р.К., Егодуров Г. С., Зангеев Б. И. и др. Расчёты на прочность элементов машиностроительных конструкций в среде Mathcad. — Cтарый Оскол: ООО “ТНТ”, 2006. — 580 с.
7. Егодуров, Г.С., Покровский А. М., Зангеев Б. И. Численные методы в задачах сопротивления материалов. — Улан-Удэ: Изд-во ВСГТУ, 2010. — 610 с.
