Рассматривается формирование общепрофессиональных компетенций бакалавров, обучающихся по направлению 230301 «Технология транспортных процессов». Приводится ряд практических примеров.
Ключевые слова: подготовка бакалавров, технология транспортных процессов, общепрофессиональные компетенции, формирование в процессе обучения.
Задачи управления транспортным средством относятся к классу задач теории управления [1..3], предусматривающих перевод системы из одного состояния в другое. Наземные транспортные средства, как правило, моделируются геометрической точкой, движущейся в двумерном пространстве с введенной в нем декартовой системой координат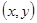 
. Траекторией точки будет кривая, задаваемая параметрическими уравнениями 
; 
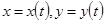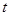- текущее время. В ряде задач возможно исключение параметра с получением более простого уравнения траектории. В общих задачах управления движению системы соответствует движение точки в многомерном пространстве. Непосредственно из физических соображений следует:
- путь системы проходит от точки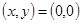 
до точки 
;
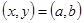- траектория лежит в заданной области плоскости;
- предусматривается минимизация некоторой целевой функции (стоимость израсходованного топлива, затраченное время, общие затраты и т. д.).
Одним из основных этапов решения задачи управления движением является формирование последовательности инструкций оператору человеко-машинной (эргатической) системы; например, путь автомобиля определяется вращением руля. Инструкция аналитически может быть определена функцией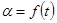 
, задающей поворот руля 
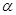от нейтрального положения в заданном направлении. Переменными состояния 
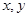задается положение и ориентация системы; переменные управления 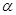фактически являются точными инструкциями оператору. Различие между указанными переменными состоит в том, что изменение 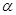ведет к изменению объекта в плоскости 
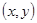, при этом значения 
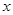и 
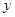непосредственно не влияют на 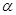(оператор по своему выбору может изменить 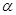в определенных пределах; невозможно вращать руль в одном направлении до бесконечности). Так, легко пришли к математическим моделям задачи управления: алгебраическим уравнениям 
;
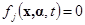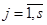или системе дифференциальных уравнений 
;
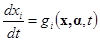векторы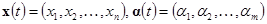 
принадлежат векторным пространствам размерносте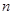й 
и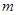 
соответственно. В одномерном пространстве положение точки определяется переменной 
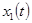, скорость — переменной 
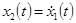, ускорение — 
.
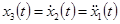Остановимся на формировании двух компетенций бакалавров, обучающихся по направлению 230301 «Технология транспортных процессов»:
- ОПК 2 (способность понимать научные основы технологических процессов в области технологии, организации, планирования и управления технической и коммерческой эксплуатацией транспортных систем);
- ОПК 3 (способность применять систему фундаментальных знаний (математических, естественнонаучных, инженерных и экономических) для идентификации, формулирования и решения технических и технологических проблем в области технологии, организации, планирования и управления технической и коммерческой эксплуатацией транспортных систем).
Для иллюстрации рассмотрим некоторые практические задачи.
Постановка неработающего автомобиля в гараж. Пусть требуется переместить автомобиль из одного положения в другое по прямой линии. В простейшем случае можно исходить из предположения, что силы сопротивления отсутствуют, имеются силы, тянущие или толкающие машину. Естественно, ускорение не должно превышать некоторой величины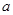 
, а замедление по абсолютной величине не превышает 
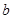; ускорение лежит в интервале 
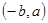. Задача заключается в определении минимального времени для прохождения данного расстояния (начальная и конечная точка соответствуют состояниям покоя). Если ускорение меньше 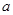или численная величина замедления меньше 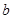, то расстояние, проходимое за данное время, уменьшается. Метод решения задачи состоит в использовании заданных ограничений для определения границ области изменения переменных с последующим отысканием решения на границах области.
При учете трения или сопротивления вязких сил уравнение движения при максимальной силе, действующей в положительном направлении, будет иметь вид
,
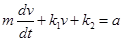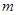- масса; ограничения накладываются на силу 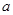, а не на ускорения. Решение должно соответствовать максимальному ускорению, сменяемому максимальным замедлением.
Для движения между двумя точками необходимо учитывать наличие максимальной безопасной скорости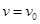 
наряду с максимальным ускорением 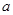и замедлением .
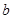Для снижения затрат горючего оператор должен добиваться максимального расхода топлива, а не максимальной скорости. Решение, при котором автомобиль движется по инерции к состоянию покоя в конце пути, будет более предпочтительным, по сравнению с тем, которое требует резкого торможения.
Маневрирование автомобилем. Рассмотрим управление транспортным средством при движении в двух измерениях. Здесь существует минимальный допустимый радиус поворота; ограничения будут накладываться на кривизну пути. Сложная траектория движения четырехколесного аппарата можно исследовать на основе кратчайших путей движения геометрической точки, траектории движений которой имеют ограниченную кривизну. Можно потребовать, чтобы полное решение состояло из прямолинейных участков (кратчайшие пути в пространстве) и отрезков окружностей минимального радиуса.
Пусть, например, автомобиль начинает движение из точки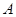 
перпендикулярно прямой 
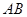, и пусть требуется определить минимальные пути от 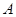до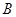 
без использования заднего хода. В частности, при 
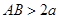движение начинается с поворота по направлению к 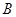по окружности радиуса 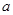. Искомым путем здесь будет 
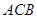, где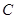 
лежит на указанной окружности, а 
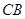— отрезок касательной к окружности в точке .
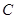На автомобильных стоянках требуется машины ставить между разметочными линиями, начерченными под различными углами. В этом случае автомобиль, расположенный в точке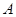 так, что он может начать под углом 
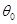к линии 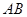, необходимо переместить в точку 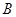, расположив его под углом 
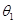к 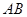(рис.1).
Рис. 1.
Метод решения состоит в определении окружностей радиуса 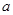, касающихся заданных направлений, как в точке 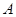, так и в точке 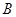. Соединив одну окружность с другой общей касательной, нетрудно определить самый короткий путь (рис.2, стрелками указаны направления движения).
Аналогично можно определить движение автомобиля при использовании заднего хода.
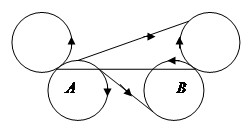
Рис. 2.
Таким образом, в работе на конкретных примерах показывается, как можно формировать общепрофессиональные компетенции бакалавров, обучающихся по направлению 230301 «Технология транспортных процессов» [4…7].
Литература:
1. Данилов А. М., Гарькина И. А. Образовательная система с позиций идентификации и управления / Региональная архитектура и строительство. — 2013. — № 2. — С. 143–146.
2. Гарькина И. А., Данилов А. М., Королев Е. В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем / Известия высших учебных заведений. Строительство. — 2009. — № 3–4. — С. 30–37.
3. Гарькина И. А., Данилов А. М., Домке Э. Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). –2011. — № 2. — С. 18–23.
4. Данилов А. М., Гарькина И. А., Маркелова И. В. Методологические принципы оценки качества образовательной системы / Современные проблемы науки и образования. — 2014. — № 2. — С. 161.
5. Гарькина И. А., Данилов А. М. Системный подход к повышению качества образования / Вестник Костромского государственного университета им. Н. А. Некрасова. Серия: Педагогика. Психология. Социальная работа. Ювенология. Социокинетика. –2013. — Т. 19. — № 4. –С. 4–7.
6. Данилов А. М., Гарькина И. А., Маркелова И. В. Междисциплинарные связи при компетентностном подходе к подготовке бакалавров / Современные проблемы науки и образования. –2014. –№ 3. — С. 188.
7. Данилов А. М., Гарькина И. А., Гарькин И. Н. Подготовка бакалавров: компетентностный подход, междисциплинарность / Региональная архитектура и строительство. — 2014. — № 2. — С. 192–199.
