В статье приведено описание и некоторые подходы к построению геометрического аппарата моделирования плоских кривых.
Ключевые слова: геометрическое моделирование, геометрический аппарат, плоские кривые.
С математической точки зрения мы привыкли рассуждать множество явлений природы аналитически. Стараемся устанавливать зависимость того или иного происходящего явления для того чтобы понять непонятное и тем самым успокоить разум. Множество подобных явлений классифицируются, группируются, систематизируются для того чтобы облегчить задачу последователей. Но природу всякого явления с геометрической стороны можно классифицировать одним названием — обстоятельство.
Мы не привыкли рассуждать множество явлений природы геометрическими образами, хотя некоторые математические описания имеют толкование геометрических образов: линейное уравнение, линейное пространство, квадратное или кубическое уравнение и т. п.
Весьма интересно толкование прямой и кривых линий второго порядка с аналитической стороны. В декартовой системе координат нельзя их объединить в один класс. Прямая есть линия первого порядка, а кривые алгебраические второго, третьего … n-го порядка. Кроме того они еще и делятся на трансцендентные. По всей видимости в декартовой системе сложно понять геометрию (природу) образования кривых, усложняется тем самым понятие естественности. В разных литературах по разному описываются природа образования кривых. Линию можно рассматривать как пересечение двух поверхностей [1], как траекторию движущейся точки на плоскости или пространстве [2]. В частности более разнообразно описываются линии в трудах Савелова А. А. [3] (имеются семь описаний).
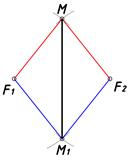
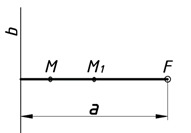
Рассмотрим обстоятельство образования плоских кривых на примерах геометрических построений. Попробуем построить аппарат геометрического моделирования для плоских кривых в отличие от декартовой системы построений. Для этого нам потребуется плоскость H — где будут отображаться плоские кривые и какие-либо условия исходя из поставленной задачи. Если линия есть след движущейся точки в пространстве, в нашем примере на плоскости то на этой плоскости требуются дополнительно еще и два рычага управления, чтобы можно было управлять кривизной линии (поворачивать в права, в влево или вверх, вниз). Следовательно, на плоскости H закрепляем две точки F1 и F2 (рис. 1), тем самым образуем геометрический аппарат моделирования для плоских кривых.
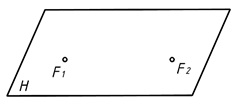
Рис. 1
Данный аппарат позволяет сформировать на нем кривые линии в частности и прямую.
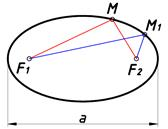
Определим положение любой точки M принадлежащей кривой через опорные точки F1 и F2. Очевидно, самое простое отношение F1M=F2M или F1M–F2M=0 определит прямую (рис. 2-а).
Отношение F1M+F2M=a (const.) всегда определяет эллипс (рис. 2-б), также как отношение в) F1M–F2M=a (const.) (рис. 2-в).
Отношение F1M/F2M=a (const.) или F1M*F2M=a (const.) определяет окружность (рис. 2-г).
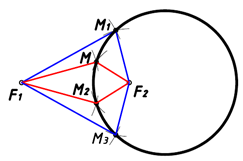
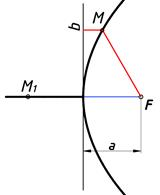
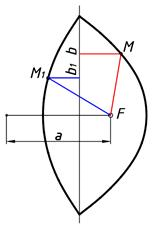
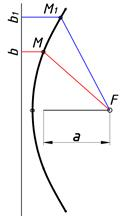
Кривая параболы на предлагаемом аппарате моделирования требует некоторого иного подхода. Для начала строится прямая b как показано на рис. 2-а или выбирается другой аппарат моделирования который состоит из плоскости H, точки F и прямой b не проходящей через данную точку. Тогда, отношение bM–F2M=0 будет удовлетворять кривой параболе (рис. 3).
|
|
|
|
а) F1M–F2M=0 Прямая |
б) F1M+F2M=a (const.) Эллипс |
|
|
|
|
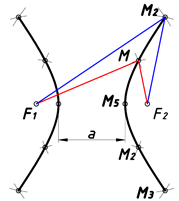
в) F1M–F2M=a (const.) Гипербола |
г) F1M/F2M=a (const.) или F1M*F2M=a (const.) Окружность |
Рис. 2
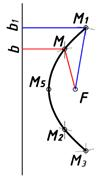
Рис. 3. Геометрическая модель параболы (bM–FM=0).
Следовательно, прямая и кривая параболы родственные линии в различных аппаратах геометрического моделирования (сравните: F1M–F2M=0 и bM–FM=0).
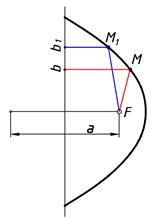
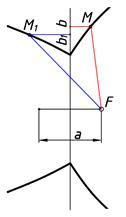
Какие кривые будут построены если будем сохранят отношения первого аппарата для второго. Важным элементом построений является параметр a по отношению к расстоянии от прямой b до точки F (рис. 4).
|
|
|
|
|
|
|
|
|
|
bM+FM=a (const.) Эллипс |
bM–FM=a (const.) Гипербола |
Рис. 4
В заключении можно сказать что методы геометрического моделирования по отношению к аналитическим преимущественно разнообразны и многовариантны для моделирования различных объектов и процессов. Кроме того они более доступны для широкого круга пользователей имеющие навыки элементарной математики, геометрии, алгебры.
Литература:
1. Выгодский М. Я. Справочник по высшей математике. — М.: Наука, 1977. — С.200.
2. Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии. — М.: Наука, 1988. — С.125.
3. Савелов А. А. Плоские кривые — систематика, свойства, применения. — М.: 1960. — 293с.