В данной работе было проведено сравнение простого метода и метода декомпозиции для расчета межотраслевого баланса, а также прогнозирование изменения уровня цен под воздействием различных факторов с помощью тензорного метода.
Модель разрабатывалась в 80-х годах 20-го века и её основной целью было уменьшить объем расчетов, так как в то время компьютеры были намного менее производительны, чем сейчас. Модель же позволяет проводить параллельные вычисления.
При данном подходе вся экономика разбивается на ряд отраслей, между которыми движутся потоки ресурсов, промежуточной и готовой продукции. Последствия изменений в конечном спросе или в условиях производства в одной отрасли изучаются через прослеживание количественной реакции всех взаимосвязанных отраслей.
Основные предпосылки анализа:
- В экономической системе производятся, потребляются и инвестируются n типов продуктов (товаров).
- Каждая отрасль является «чистой», т. е. производит только один тип продукта. Различные отрасли производят различные типы продуктов. Таким образом, n отраслей и n типов продуктов находятся во взаимно однозначном соответствии.
- Основным элементом модели является квадратная матрица технологических элементов (или матрица прямых затрат) размерности nхn: А = 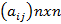 . Числа
. Числа 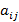 показывают сколько продукции отрасли i необходимо затратить для производства единицы продукции отрасли j.
показывают сколько продукции отрасли i необходимо затратить для производства единицы продукции отрасли j.
Основное допущение модели заключается в том, что технологические коэффициенты (прямые затраты) остаются постоянным вне зависимости от масштаба производства, т. е. предполагается постоянная эффективность от укрупнения масштаба производства. Кроме того, в процессе производства исключается взаимозаменяемость ресурсов, они должны находиться в строгой пропорции (производственная функция Леонтьева).
Пусть  — выпуск i-го продукта в единицу времени, например, за год. Эта величина представляет собой валовой выпуск (валовой продукт). Он распадается на две части:
— выпуск i-го продукта в единицу времени, например, за год. Эта величина представляет собой валовой выпуск (валовой продукт). Он распадается на две части:
- производственное потребление во всех отраслях;
- конечное (непроизводственное) потребление.
Производственное потребление i-го продукта всеми отраслями равно:
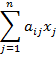
Тогда конечное потребление i-го продукта, которое мы будем обозначать 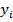 , составит:
, составит:
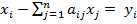 , i = 1,..., n. (1)
, i = 1,..., n. (1)
Полученная система уравнений и представляет собой модель Леонтьева. Модель Леонтьева можно представить в матричной форме. Для этого введем следующие обозначения: х- вектор валового выпуска; y — вектор конечного потребления (чистого выпуска); А — матрица прямых затрат.
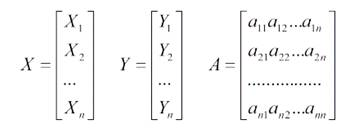
Тогда можно записать:
x — Ax = y (1)
Величины xi, aij и yi могут быть представлены в натуральных или стоимостных единицах измерения, в соответствии с этим различают натуральный или стоимостной межотраслевые балансы. Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного потребления y. По очевидным экономическим соображениям и коэффициенты, и переменные модели Леонтьева должны быть неотрицательными. Разрешимость системы в неотрицательных величинах означает работоспособность или продуктивность модели Леонтьева.
Данная работа представляет собой расчет выпуска отраслей в целом по экономике с применением двух методов: простого метода расчета и метода декомпозиции. Простой метод расчета описывается следующим образом:
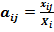 ;
;
Е — А;
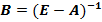 ;
;
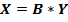 , где
, где 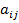 — элементы матрицы прямых затрат,
— элементы матрицы прямых затрат, 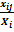 — отношение использования ресурсов отрасли на выпуск отрасли, А — матрица прямых затрат, (Е — А) — единичная матрица, B — матрица полных затрат, Y — вектор конечного потребления, Х — вектор выпуска отраслей.
— отношение использования ресурсов отрасли на выпуск отрасли, А — матрица прямых затрат, (Е — А) — единичная матрица, B — матрица полных затрат, Y — вектор конечного потребления, Х — вектор выпуска отраслей.
В соответствии с методом декомпозиции, экономику можно поделить на подсети (к примеру, подсеть промышленности, подсеть торговли, подсеть добычи полезных ископаемых). Главная цель метода — сократить время вычисления МОБ. Разделив матрицу на подсети, мы можем проводить параллельные вычисления (расчет каждой подсети на отдельном компьютере). Разделив матрицу на подсети, у нас есть 2 способа расчета МОБ — простой и сложный. В данной работе был использован простой метод. Данный метод позволяет уменьшить время расчета МОБ, так как после разделения матрицы на подсети, каждая сеть считается по отдельности. После разделения матрицы на подсети проводятся параллельные вычисления для каждой подсети. Данный метод произведен в двух этапах.
Полученные данные расчетов выпуска отраслей при использовании метода декомпозиции показали, что результаты отклонений от отчетных данных выпуска отраслей в первом и во втором случаях значительны в расхождениях. При использовании второго этапа расчета выпуска отраслей значения отклонений малы (1,66 %), с первым этапом (12,57 %).
Представленная работа оснащена также и построением двойственной задачи к полученной модели «Затраты-Выпуск».
Двойственную задачу можно записать следующим образом:
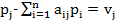 , j = 1, …, n. (2)
, j = 1, …, n. (2)
где pj — цена на единицу продукции вида j; vj — добавленная стоимость на единицу выпуска j-й отрасли. Или в матричной форме
p — AT p = v (3)
Добавленная стоимость включает в себя оплату труда работников, валовую прибыль, валовой смешанный доход, чистые налоги на производство. С этой целью производится нахождение доли ВДС (ВДС/всего использовано отечественных товаров и услуг).
Автором были рассмотрены несколько ситуаций, которые поспособствовали тому, что было проанализировано изменение цены при изменении величины ВДС.
Первая ситуация, а она же стандартная, учитывает налоги и субсидии. На основании полученных результатов получен вывод о том, что при данных существующей матрицы и уровня ВДС принимается индекс цен, равный 1. То есть, в данном случае цены не изменились, считается также, что данная ситуация является отчетной.
Моделируется следующая ситуация, в которой не учитываются субсидии, например, в сельском хозяйстве и жкх. Итог: цены на с/х вырастут на 8,5 %, на жкх — 14,5 %. Также цены изменятся и на те отрасли, которые каким-либо образом связаны с определяемыми отраслями. Это связано с тем, что существует значительная корреляция данной отрасли с отраслью с/х.
Для третьей ситуации происходит искусственное увеличение уровня ОТР на 20 %. В наибольшей степени изменятся цены в таких отраслях, как образование, здравоохранение и предоставление социальных услуг, и предоставление коммунальных, социальных и персональных услуг. В наименьшей степени увеличение цен коснется следующих отраслей: добыча полезных ископаемых, кроме топливно-энергетических и производства транспортных средств и оборудования.
Для этой ситуации можно, к примеру, определить изменение цены при уменьшении ОТР на 10 %. Итого: при изменении уровня ОТР на 10 % в сторону понижения, наблюдается картина следующего понижения цены: в таких отраслях, как здравоохранение и предоставление социальных услуг, образование, государственное управление, цены снизятся на максимальные значения — 9,2 %, 8,9 %, 7,4 % соответственно. В следующих отраслях, рыболовство, рыбоводство и предоставление услуг в этих отраслях, добыча топливно-энергетических полезных ископаемых, химическое производство и некоторых других, будет получено минимальное изменение уровня цен.
Выводы
Использование метода декомпозиции показало, что в соответствии с моделью «Затраты-Выпуск», экономика делится на подсети: промышленность, сельское хозяйство, строительство, транспорт, розничная торговля. Суть состоит в том, что экономику можно поделить на подсети, в каждой подсети отрасли сильно взаимосвязаны, а взаимодействие подсетей представляет сеть пресечений.
В соответствии с А. Петровым в экономике отрасли не сильно связаны между собой: «В задачах, где рассматриваются десятки и сотни, а тем более тысячи отраслей (предприятий), экономическая матрица весьма слабо заполнена ненулевыми элементами, т. е. немногие отрасли связаны между собой» [1, с. 45].
В этом и состоит сложность. А. Е. Петров утверждает, что отрасли в экономике слабо связаны между собой, но в данном случае почти каждая отрасль использует продукт другой отрасли. Таким образом, все отрасли тесным образом связаны между собой, а не только в своей подсети. В соответствии с Петровым сеть пересечений должна быть примерно такого же размера, что и подсети. В проведенном же расчете, сеть пересечений по размерности не отличалась от исходной матрицы. Уменьшение матрицы было бы возможно только в том случае, если бы продукт какой-нибудь отрасли использовался только внутри подсети, и между собой подсети были бы связаны только через некоторые отрасли, однако все отрасли связаны между собой.
Однако это не значит, что данный метод неправилен. В цитате А. Е. Петрова речь идет о сотнях или даже тысячах отраслях. В данной работе приведены только 30 отраслей, так как именно столько отраслей в своих сборниках предлагает Белорусский статистический комитет. Если бы происходило большее дробление на отрасли, то, возможно, матрица бы сильнее заполнялась нулевыми элементами, сеть пересечений бы уменьшалась, расчеты бы больше соответствовали настоящим.
Метод дает преимущество только для больших экономик: Россия, США, Китай.
Обобщение полученных выводов по нахождению корреляционных отношений цен на товары и услуги и различных уровней ВДС, позволяет утверждать, что данная модель позволяет получить достаточно достоверные прогнозные значения для возможной ситуации экономического характера. Моделирование и анализ потенциально-существующих случаев изменения того или иного показателя способствует формированию направленной на погашение негативных последствий данных изменений экономической политики.
Литература:
1. Крон Г. «Тензорный анализ сетей» — под. Ред. Л. Т. Кузина, П. Г. Кузнецова. М: Сов. Радио, 1978. — 720 с.
2. А. Е. Петров Сетевые методы планирования производства: учебно-методическое пособие — М.: МГГУ, 2011. — 148 с.
3. Эконометрика: учебник/ И. И. Елисеева, С. В. Курышева, Т. В. Костеева и др.; под ред. И. И. Елисеевой. — 2-е изд., перераб. — М: Финансы и статистика, 2007. — 576 с.
4. В. И. Степанов, А. Ф. Терпугов: Экономико-математическое моделирование. — М.: Академия, 2009. — 112 с.







