В данной работе приведен результат математического моделирования синхронного явнополюсного линейного двигателя (СЯЛД) с помощью магнитных и электрических схем замещения [1]. В пазах индуктора (Z1 = 6) расположена классическая трехфазная обмотка с нулевым проводом [2]. Всё пространство подвижного элемента (ротора) разбито на 12 частей, соответствующих зубцовому делению индуктора, как показано на рис. 2. Ширина полюса в данной работе принята равной ширине междуполюсного пространства с обмотками постоянного тока.
Так как работа адресована студентам, то для лучшего овладения материалом выводы математических формул даны без сокращений.
Запишем основные уравнения для «n»-ого участка схемы замещения (рис. 1).
Баланс магнитных напряжений магнитной цепи
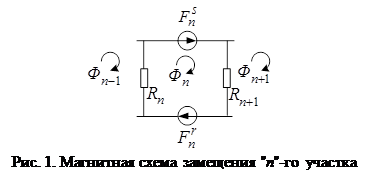
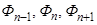 – контурные магнитные потоки;
– контурные магнитные потоки;
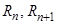 – магнитные сопротивления воздушных участков;
– магнитные сопротивления воздушных участков;
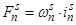 – магнитодвижущая сила, созданная статорным током
– магнитодвижущая сила, созданная статорным током 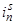 , протекающим по всем проводникам паза (
, протекающим по всем проводникам паза (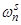 );
);
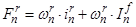 – М.Д.С. тока в обмотке подвижного элемента (ротора);
– М.Д.С. тока в обмотке подвижного элемента (ротора);
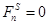 – в шунтирующих зонах.
– в шунтирующих зонах.
Баланс М.Д.С. для «n»-го участка имеет следующий вид:
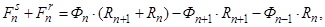
где 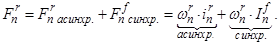
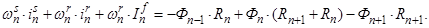
Ток 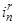 условно назовем асинхронной составляющей полного тока в роторной обмотке. Этот ток создается от Э.Д.С. трансформации, Э.Д.С. движения, от изменяющегося потока во времени или от движущего потока в пространстве [4], [5], …, [11].
условно назовем асинхронной составляющей полного тока в роторной обмотке. Этот ток создается от Э.Д.С. трансформации, Э.Д.С. движения, от изменяющегося потока во времени или от движущего потока в пространстве [4], [5], …, [11].
Вторая составляющая М.Д.С. (условно назовем синхронная составляющая 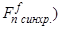 представляет собой бегущую в пространстве ступенчатую фигуру в соответствии с дискретным расположением роторной обмотки.
представляет собой бегущую в пространстве ступенчатую фигуру в соответствии с дискретным расположением роторной обмотки.
В данной работе синхронную составляющую выразим 1-й гармоникой бегущей волны:
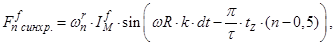
где 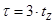 - полюсное деление;
- полюсное деление;
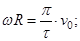
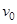 - линейная скорость
- линейная скорость 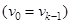 .
.
Отсюда асинхронная составляющая тока в обмотке ротора определится по следующему выражению:
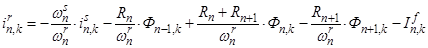 . (1)
. (1)
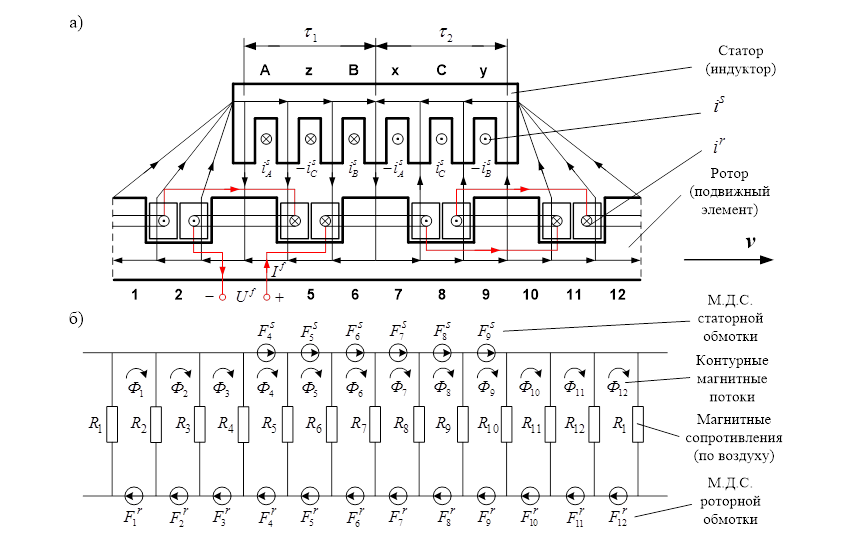
Рис. 2. а) Синхронный явнополюсный линейный двигатель (2р = 2, Z1 = 6); б) Магнитная схема замещения
Уравнение баланса напряжений электрической цепи ротора для асинхронной составляющей тока ротора
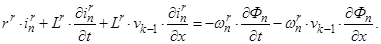 (2)
(2)
Выразим производные во времени через конечные разности:
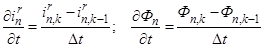 ,
,
где n – номер зубцового деления;
k – номер шага разбиения по времени.
В формуле (2) линейную скорость ротора принимаем равной 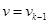 и в пределах «k» интервала считается постоянным.
и в пределах «k» интервала считается постоянным.
Производные по пространственной координате «х» выразим через центральные конечные разности:
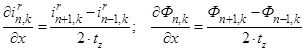 .
.
С учетом вышеприведенных замечаний уравнение (2) примет следующий вид:
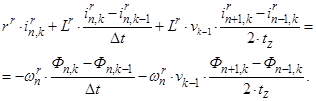 (3)
(3)
Исключим из уравнения (3) асинхронную составляющую тока в роторе. Для этого подставим выражение (1) в уравнение (3) и получим:
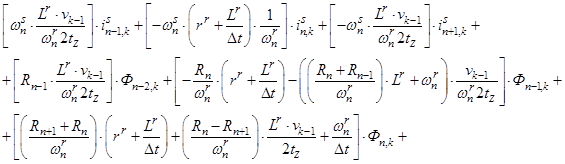
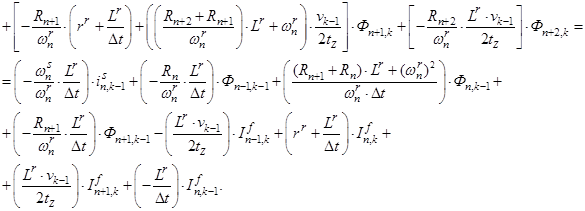 (4)
(4)
Это уравнение может быть реализовано при произведении матрицы А, элементы которой записаны в квадратных скобках, на матрицу-столбец X, состоящей из потоков (Ф) и токов статорной обмотки. Правая часть уравнения (4) формирует первые двенадцать элементов матрицы-столбца свободных членов S в (k-1) момент времени. Элементы 13, 14 и 15 строк матрицы А и соответствующие элементы s13, s14 и s15 будут сформированы из баланса напряжений статорной обмотки.
Наконец, последние элементы матриц А и S определятся из баланса токов в трехфазной обмотке соединенной в звезду с нулевым проводом. Матрица-столбец Х сформирована из первых двенадцати элементов, соответствующих потокам Ф1, … , Ф12, а остальные – токам статорной обмотки iАs, iСs, iВs и i0s.
Общий вид матриц при числе полюсов 2р = 2 и общем числе пазов индуктора (статора) Z1 = 6 приведен на рис. 3.
Введем следующие обозначения:
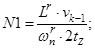
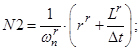
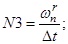
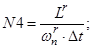
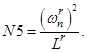
- Магнитные сопротивления в шунтирующих зонах:
R1 = 500∙Rδ;
R2 = R12 = 50∙Rδ;
R3 = R11 = 5∙Rδ.
- Магнитные сопротивления в индукторной зоне:
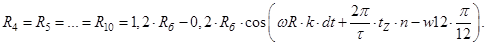
- Элементы матрицы А, перемножаемые на потоки матрицы-столбца Х:
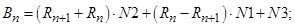
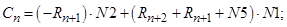
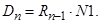
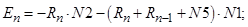
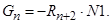
- Элементы матрицы А, перемножаемые на токи матрицы Х:
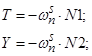
- Элементы матрицы-столбца свободных членов S:
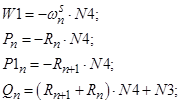
С учетом вышеприведенных обозначений (N1, N2, …, N5, T, Y, W1, P, P1, Q) уравнение 4 приобретет следующий вид:
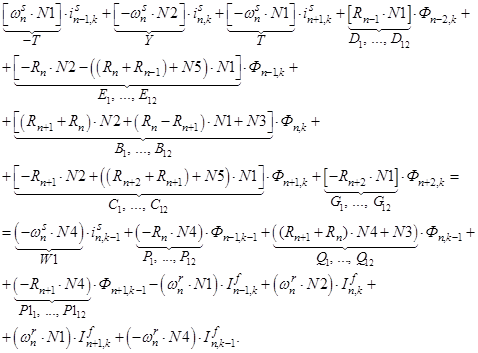 (4’)
(4’)
После подстановки в (4’) выражений (T, Y, Dn, En, Bn, Cn, Gn) получаем простое выражение удобное для программирования:
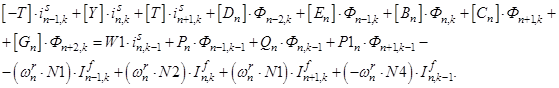 (4”)
(4”)
Линейная токовая нагрузка в роторной обмотке в k и k-1 моменты времени:
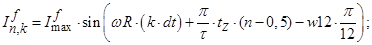
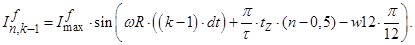
Уравнение (4) позволит определить для первых двенадцати строк элементы матрицы А и с первый по двенадцатый элементы матрицы-столбца S, для этого последовательно зададимся n:
n = 1.
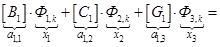
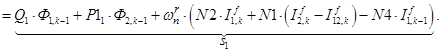
Запишем элементы матрицы А:
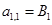 ;
; 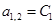 ;
; 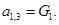
В правой части сформирован элемент 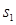 матрицы-столбца S:
матрицы-столбца S:
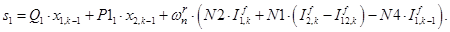
Примечание: вначале матрица А предстанет «пустой» и после каждой операции 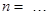 определятся постепенно элементы для каждой строки и только в конце всех операций матрица А предстанет перед читателем в том виде как она дана на рис. 3. Но эта «пустая» матрица А уже должна быть подготовлена. Эта «пустая» форма направляет, выступает «организующим началом» по поиску элементов в каждой строке.
определятся постепенно элементы для каждой строки и только в конце всех операций матрица А предстанет перед читателем в том виде как она дана на рис. 3. Но эта «пустая» матрица А уже должна быть подготовлена. Эта «пустая» форма направляет, выступает «организующим началом» по поиску элементов в каждой строке.
При n = 1, как было показано выше, определились элементы первой строки. Найденные коэффициенты вписываем в матрицу А. В дальнейшем становится понятным алгоритм заполнения матрицы.
n = 2.
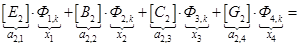
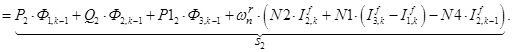
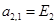 ;
; 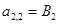 ;
; 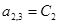 ;
; 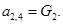
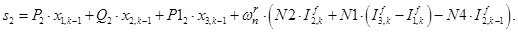
n = 3.
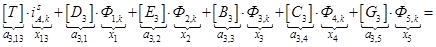
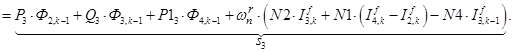
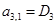 ;
; 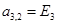 ;
; 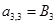 ;
; 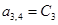 ;
; 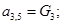
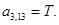
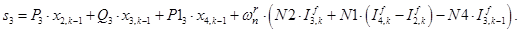
Примечание: при подстановке в уравнение (4) n = 4, мы увидим в соответствии с рис. 1, что войдет ток iСS с отрицательным знаком, в то же время в матрице-столбце Х нет знака «–» , поэтому его необходимо учесть в соответствующем элементе матрицы А.
Аналогично для других фаз, в концах обмоток x, y, z условно принимаем знак «–» и этот знак вводим в соответствующие элементы матрицы А.
n = 4.
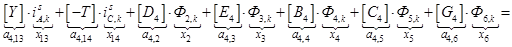
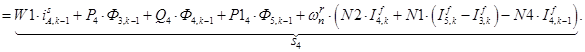
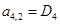 ;
; 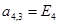 ;
; 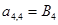 ;
; 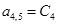 ;
; 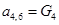 ;
; 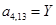 ;
; 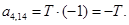
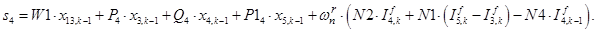
n = 5.
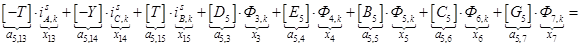
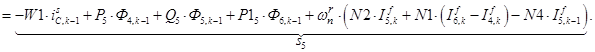
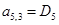 ;
; 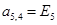 ;
; 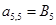 ;
; 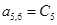 ;
; 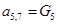 ;
; 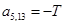 ;
;
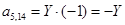 ;
; 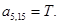
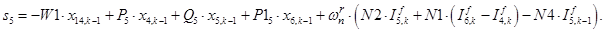
|
|
Матрица А |
|
Х |
|
S |
|||||||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
|
|
|
1 |
a1,1 |
a1,2 |
a1,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
×
|
x1 = Ф1 |
=
|
s1 |
|
2 |
a2,1 |
a2,2 |
a2,3 |
a2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 = Ф2 |
s2 |
||
|
3 |
a3,1 |
a3,2 |
a3,3 |
a3,4 |
a3,5 |
|
|
|
|
|
|
|
a3,13 |
|
|
|
x3 = Ф3 |
s3 |
||
|
4 |
|
a4,2 |
a4,3 |
a4,4 |
a4,5 |
a4,6 |
|
|
|
|
|
|
a4,13 |
a4,14 |
|
|
x4 = Ф4 |
s4 |
||
|
5 |
|
|
a5,3 |
a5,4 |
a5,5 |
a5,6 |
a5,7 |
|
|
|
|
|
a5,13 |
a5,14 |
a5,15 |
|
x5 = Ф5 |
s5 |
||
|
6 |
|
|
|
a6,4 |
a6,5 |
a6,6 |
a6,7 |
a6,8 |
|
|
|
|
a6,13 |
a6,14 |
a6,15 |
|
x6 = Ф6 |
s6 |
||
|
7 |
|
|
|
|
a7,5 |
a7,6 |
a7,7 |
a7,8 |
a7,9 |
|
|
|
a7,13 |
a7,14 |
a7,15 |
|
x7 = Ф7 |
s7 |
||
|
8 |
|
|
|
|
|
a8,6 |
a8,7 |
a8,8 |
a8,9 |
a8,10 |
|
|
a8,13 |
a8,14 |
a8,15 |
|
x8 = Ф8 |
s8 |
||
|
9 |
|
|
|
|
|
|
a9,7 |
a9,8 |
a9,9 |
a9,10 |
a9,11 |
|
|
a9,14 |
a9,15 |
|
x9 = Ф9 |
s9 |
||
|
10 |
|
|
|
|
|
|
|
a10,8 |
a10,9 |
a10,10 |
a10,11 |
a10,12 |
|
|
a10,15 |
|
x10 = Ф10 |
s10 |
||
|
11 |
|
|
|
|
|
|
|
|
a11,9 |
a11,10 |
a11,11 |
a11,12 |
|
|
|
|
x11 = Ф11 |
s11 |
||
|
12 |
|
|
|
|
|
|
|
|
|
a12,10 |
a12,11 |
a12,12 |
|
|
|
|
x12 = Ф12 |
s12 |
||
|
13 |
|
|
|
a13,4 |
|
|
a13,7 |
|
|
|
|
|
a13,13 |
|
|
|
x13 = iАS |
s13 |
||
|
14 |
|
|
|
|
|
a14,6 |
|
|
a14,9 |
|
|
|
|
|
a14,15 |
|
x14 = iСS |
s14 |
||
|
15 |
|
|
|
|
a15,5 |
|
|
a15,8 |
|
|
|
|
|
a15,14 |
|
|
x15 = iВS |
s15 |
||
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
a16,13 |
a16,14 |
a16,15 |
a16,16 |
x16 = i0S |
s16 |
||
Рис. 3. Общий вид матриц A, X и S.
n = 6.
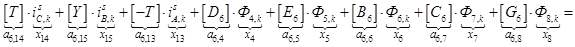
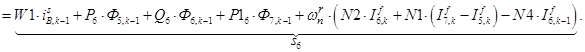
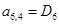 ;
; 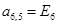 ;
; 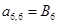 ;
; 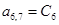 ;
; 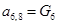 ;
; 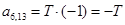 ;
;
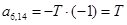 ;
; 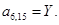
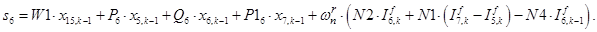
n = 7.
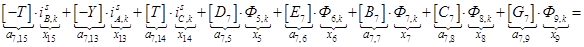
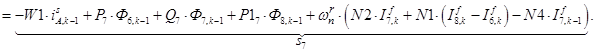
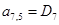 ;
; 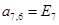 ;
; 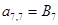 ;
; 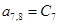 ;
; 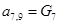 ;
; 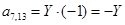 ;
;
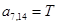 ;
; 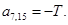
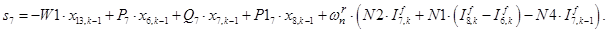
n = 8.
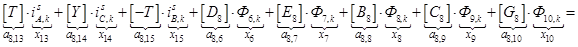
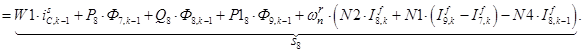
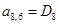 ;
; 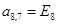 ;
; 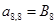 ;
; 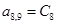 ;
; 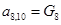 ;
; 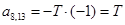 ;
;
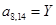 ;
; 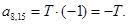
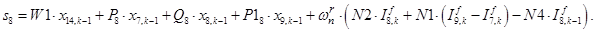
n = 9.
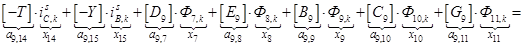
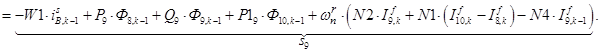
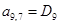 ;
; 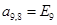 ;
; 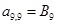 ;
; 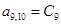 ;
; 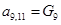 ;
; 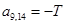 ;
; 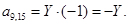
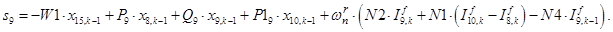
n = 10.
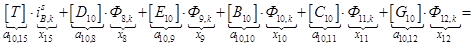
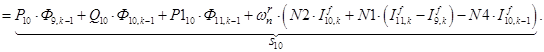
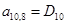 ;
; 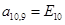 ;
; 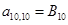 ;
; 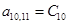 ;
; 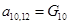 ;
; 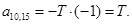
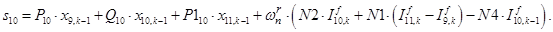
n = 11.
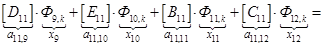
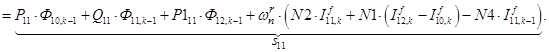
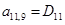 ;
; 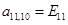 ;
; 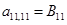 ;
; 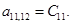
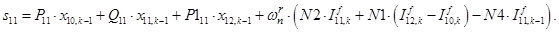
n = 12.
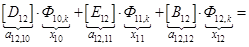
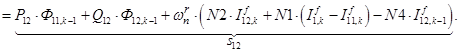
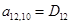 ;
; 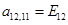 ;
; 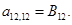
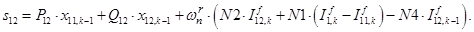
Элементы строк 13 и 14 и 15 матрицы А и соответствующие элементы матрицы-столбца S определяются из баланса электрических напряжений обмоток статора.
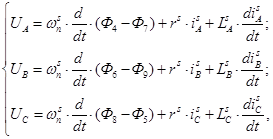 (5)
(5)
где 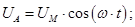
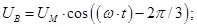 (6)
(6)
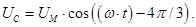
С учетом шага по времени ∆t в k-ый момент времени:
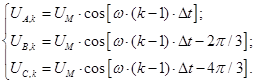 (7)
(7)
n = 13.
Выразим производные тока 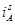 , потоков
, потоков 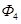 и
и 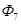 через конечные разности:
через конечные разности:
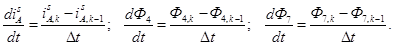
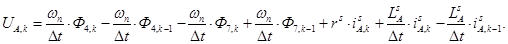
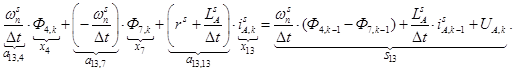
Обозначим 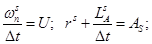
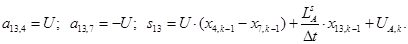
Аналогично для строк 14 и 15:
n = 14.
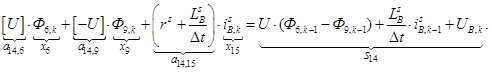
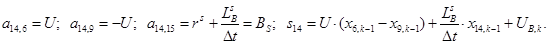
n = 15.
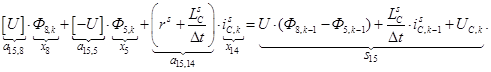
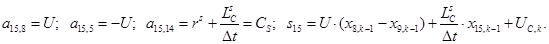
n = 16.
Наконец, сумма токов определяет элементы шестнадцатой строки матрицы А и элемент 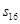 матрицы-столбца S.
матрицы-столбца S.
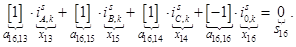
Окончательно, матрица А примет следующий вид, удобный для программирования в MATLAB (рис. 4):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
1 |
B1 |
C1 |
G1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
E2 |
B2 |
C2 |
G2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
D3 |
E3 |
B3 |
C3 |
G3 |
|
|
|
|
|
|
|
T |
|
|
|
|
4 |
|
D4 |
E4 |
B4 |
C4 |
G4 |
|
|
|
|
|
|
Y |
-T |
|
|
|
5 |
|
|
D5 |
E5 |
B5 |
C5 |
G5 |
|
|
|
|
|
-T |
-Y |
T |
|
|
6 |
|
|
|
D6 |
E6 |
B6 |
C6 |
G6 |
|
|
|
|
-T |
T |
Y |
|
|
7 |
|
|
|
|
D7 |
E7 |
B7 |
C7 |
G7 |
|
|
|
-Y |
T |
-T |
|
|
8 |
|
|
|
|
|
D8 |
E8 |
B8 |
C8 |
G8 |
|
|
T |
Y |
-T |
|
|
9 |
|
|
|
|
|
|
D9 |
E9 |
B9 |
C9 |
G9 |
|
|
-T |
-Y |
|
|
10 |
|
|
|
|
|
|
|
D10 |
E10 |
B10 |
C10 |
G10 |
|
|
T |
|
|
11 |
|
|
|
|
|
|
|
|
D11 |
E11 |
B11 |
C11 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
D12 |
E12 |
B12 |
|
|
|
|
|
13 |
|
|
|
U |
|
|
-U |
|
|
|
|
|
AS |
|
|
|
|
14 |
|
|
|
|
|
U |
|
|
-U |
|
|
|
|
|
BS |
|
|
15 |
|
|
|
|
-U |
|
|
U |
|
|
|
|
|
CS |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
-1 |
Рис. 4.
Неизвестные переменные (потоки и токи в статорной обмотке) в k-й момент времени определяются в результате следующей операции с матрицами:
X=A-1·S.
Далее, подставляя в уравнение (1) n = 1…12, определяем суммарные токи (М.Д.С.) в роторе:
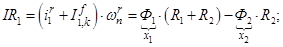
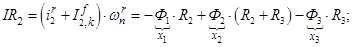
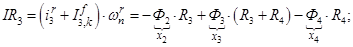
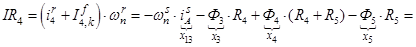
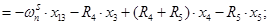
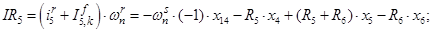
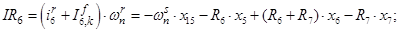
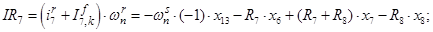
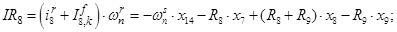
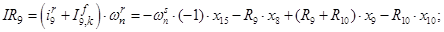
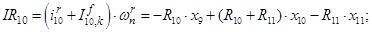
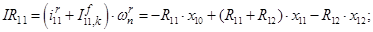
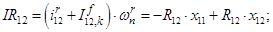
Электромагнитные усилия на зубцовом делении определяются по следующим формулам:
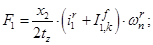
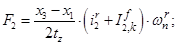
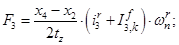
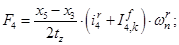
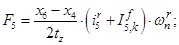
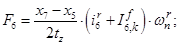
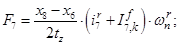
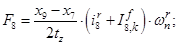
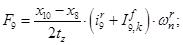
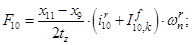
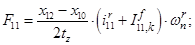
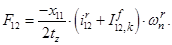
Суммарное усилие: 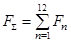 .
.
Линейная скорость ротора в k-й момент времени: 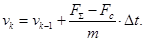
Математическая модель синхронного явнополюсного линейного двигателя реализована в программном пакете MATLAB методом Гаусса-Жордана. Ниже приведен пример расчета.
% Математическая модель СЯЛД с укладкой статорной обмотки классическим
% способом (z=6) с нулевым проводом
% function SLD_z6_zero
% Исходные данные синхронного двигателя
Rb=0.1003*10^7;
rs=4.94;
LsA=0.111;
LsB=0.114;
LsC=0.105;
rr=27;
Lr=0.074;
dt=0.001;
As=rs+LsA/dt;
Bs=rs+LsB/dt;
Cs=rs+LsC/dt;
tz=9.769*10^-3;
tau=3*tz;
m=95;
v0=0;
wns=200;
wnr=2000;
UA=wns/dt;
X=zeros(16,1);
F=0;
w12=2;
mass_Um=0;
mass_f=0;
mass_t=0;
Ukon=400;
Unach=8;
tk=8;
K=input('Длительность цикла k=');
for k=1:(K+1)
if ((k*dt >= 0) && (k*dt <= tk))
fc=k*dt*40/tk;
vs=2*tau*fc;
w=2*pi*vs/(2*tau);
eps=0.1;
if (vs-v0)>eps
ss=(vs-v0)/vs;
wR=2*pi*v0/(2*tau);
else
wR=w;
end;
Um=Unach+((Ukon-Unach)*(k*dt)^1)/((tk)^1);
end;
if (k*dt > tk)
fc=40+2*((tanh(k*dt-1)^0.6))*0;
vs=2*tau*fc;
w=2*pi*vs/(2*tau);
eps=0.1;
if (vs-v0)>eps
ss=(vs-v0)/vs;
wR=2*pi*v0/(2*tau);
else
wR=w;
end;
Um=Ukon+10*((tanh(k*dt-1)^0.6))*0;
end;
if ((k*dt >= 0) && (k*dt <= 4))
Fc=2;
end;
if (k*dt > 4)
Fc=10;
end;
if ((k*dt >= 0) && (k*dt <= 1.5))
Ufm=k*dt*2/1.5;
Ifm=Ufm/rr;
end;
if (k*dt > 1.5)
Ufm=2;
Ifm=Ufm/rr;
end;
v(1,k)=v0; %Создание вектор-строки для графика скорости
f(1,k)=sum(F)-Fc; %Создание вектор-строки для графика усилия
Ua=Um*cos(w*(k-1)*dt);
Ub=Um*cos(w*(k-1)*dt-2*pi/3);
Uc=Um*cos(w*(k-1)*dt-4*pi/3);
i0(1,k)=X(16);
i_a(1,k)=X(13);
i_b(1,k)=X(15);
i_c(1,k)=X(14);
% Формирование матрицы A
A=zeros(16);
N1=Lr*v0/(wnr*2*tz);
N2=(rr+Lr/dt)/wnr;
N3=wnr/dt;
N4=Lr/(wnr*dt);
N5=(wnr^2)/Lr;
R(1)=500*Rb;
R(2)=50*Rb;
R(3)=5*Rb;
for n=4:10
R(n)=1.2*Rb-0.2*Rb*cos(wR*k*dt+(2*pi*tz*n)/tau-w12*pi/12);
end;
R(11)=5*Rb;
R(12)=50*Rb;
R(13)=500*Rb;
R(14)=50*Rb;
A(12,12)=(R(12)*N2+N1*(R(12))+N3; %B
for n=1:11
A(n,n)=(R(n)+R(n+1))*N2+N1*(R(n)-R(n+1))+N3; %B
end;
for n=2:12
A(n,n-1)=-R(n)*N2-N1*(R(n-1)+R(n)+N5); %E
end;
A(11,12)=-R(12)*N2+N1*(R(12)+N5); %C
for n=1:10
A(n,n+1)=-R(n+1)*N2+N1*(R(n+1)+R(n+2)+N5); %C
end;
for n=3:12
A(n,n-2)=R(n-1)*N1;% D
end;
for n=1:10
A(n,n+2)=-R(n+2)*N1; %G
end;
W1=-wns*N4;
T=-wns*N1;
Y=-wns*N2;
for n=1:12
If(n)=Ifm*sin(wR*k*dt+(pi/3)*(n-0.5)-w12*pi/12);
If1(n)=Ifm*sin(wR*(k-1)*dt+(pi/3)*(n-0.5)-w12*pi/12);
end;
for n=1:3
A(n+2,n+12)=(-1)^(n+1)*T;
A(n+3,n+12)=(-1)^(n+1)*Y;
A(n+4,n+12)=(-1)^n*T;
A(n+5,n+12)=(-1)^n*T;
A(n+6,n+12)=(-1)^n*Y;
A(n+7,n+12)=(-1)^(n+1)*T;
end;
for n=1:3
A(16,n+12)=1;%hh
end;
A(16,16)=-1;%jgj
A(13,4)=UA;
A(14,6)=UA;
A(15,8)=UA;
A(13,7)=-UA;
A(14,9)=-UA;
A(15,5)=-UA;
A(13,13)=As;
A(14,15)=Bs;
A(15,14)=Cs;
% Матрица свободных членов
S=[ ((R(1)+R(2))*N4+N3)*X(1)-N4*(R(2)*X(2))-
N1*wnr*If(12)+N2*wnr*If(1)+N1*wnr*If(2)-N4*wnr*If1(1); %1
((R(2)+R(3))*N4+N3)*X(2)-N4*(R(2)*X(1)+R(3)*X(3))-N1*wnr*If(1)+N2*wnr*If(2)+N1*wnr*If(3)-N4*wnr*If1(2); %2
((R(3)+R(4))*N4+N3)*X(3)-N4*(R(3)*X(2)+R(4)*X(4))-N1*wnr*If(2)+N2*wnr*If(3)+N1*wnr*If(4)-N4*wnr*If1(3); %3
W1*X(13)+((R(4)+R(5))*N4+N3)*X(4)-N4*(R(4)*X(3)+R(5)*X(5))-N1*wnr*If(3)+N2*wnr*If(4)+N1*wnr*If(5)-N4*wnr*If1(4); %4
(-1)*W1*X(14)+((R(5)+R(6))*N4+N3)*X(5)-N4*(R(5)*X(4)+R(6)*X(6))-N1*wnr*If(4)+N2*wnr*If(5)+N1*wnr*If(6)-N4*wnr*If1(5); %5
W1*X(15)+((R(6)+R(7))*N4+N3)*X(6)-N4*(R(6)*X(5)+R(7)*X(7))-N1*wnr*If(5)+N2*wnr*If(6)+N1*wnr*If(7)-N4*wnr*If1(6); %6
(-1)*W1*X(13)+((R(7)+R(8))*N4+N3)*X(7)-N4*(R(7)*X(6)+R(8)*X(8))-N1*wnr*If(6)+N2*wnr*If(7)+N1*wnr*If(8)-N4*wnr*If1(7); %7
W1*X(14)+((R(8)+R(9))*N4+N3)*X(8)-N4*(R(8)*X(7)+R(9)*X(9))-N1*wnr*If(7)+N2*wnr*If(8)+N1*wnr*If(9)-N4*wnr*If1(8); %8
(-1)*W1*X(15)+((R(9)+R(10))*N4+N3)*X(9)-N4*(R(9)*X(8)+R(10)*X(10))-N1*wnr*If(8)+N2*wnr*If(9)+N1*wnr*If(10)-N4*wnr*If1(9); %9
((R(10)+R(11))*N4+N3)*X(10)-N4*(R(10)*X(9)+R(11)*X(11))-N1*wnr*If(9)+N2*wnr*If(10)+N1*wnr*If(11)-N4*wnr*If1(10); %10
((R(11)+R(12))*N4+N3)*X(11)-N4*(R(11)*X(10)+R(12)*X(12))-N1*wnr*If(10)+N2*wnr*If(11)+N1*wnr*If(12)-N4*wnr*If1(11); %11
((R(12))*N4+N3)*X(12)-N4*(R(12)*X(11))-N1*wnr*If(11)+N2*wnr*If(12)+N1*wnr*If(1)-N4*wnr*If1(12); %12
UA*(X(4)-X(7))+(LsA/dt)*X(13)+Ua; %13
UA*(X(6)-X(9))+(LsB/dt)*X(15)+Ub; %14
UA*(X(8)-X(5))+(LsC/dt)*X(14)+Uc; %15
0]; %16
% Решение методом Гаусса-Жордана
Z=rref([A S]); %Приведение расширенной матрицы к треугольному виду
X=Z(1:16,17:17); %Выделение последнего столбца из матрицы
% Ток в роторе
IR=[ (R(1)+R(2))*X(1)-R(2)*X(2); %1
(R(2)+R(3))*X(2)-R(3)*X(3)-R(2)*X(1); %2
(R(3)+R(4))*X(3)-R(4)*X(4)-R(3)*X(2); %3
-wns*X(13)+(R(4)+R(5))*X(4)-R(5)*X(5)-R(4)*X(3); %4
wns*X(14)+(R(5)+R(6))*X(5)-R(6)*X(6)-R(5)*X(4); %5
-wns*X(15)+(R(6)+R(7))*X(6)-R(7)*X(7)-R(6)*X(5); %6
wns*X(13)+(R(7)+R(8))*X(7)-R(8)*X(8)-R(7)*X(6); %7
-wns*X(14)+(R(8)+R(9))*X(8)-R(9)*X(9)-R(8)*X(7); %8
wns*X(15)+(R(9)+R(10))*X(9)-R(10)*X(10)-R(9)*X(8); %9
(R(10)+R(11))*X(10)-R(11)*X(11)-R(10)*X(9); %10
(R(11)+R(12))*X(11)-R(12)*X(12)-R(11)*X(10); %11
R(12)*X(12)-R(12)*X(11)]; %12
% Электромагнитное усилие
F(1)=(X(2)*IR(1))/(2*tz);
for n=1:10
F(n+1)=(X(n+2)-X(n))*(IR(n+1))/(2*tz);
end;
F(12)=(-X(11)*IR(12))/(2*tz);
% Скорость
v0=v0+((sum(F)-Fc)/m)*dt;
mass_Um(k)=Um;
mass_fc(k)=fc;
mass_t(k)=k*dt;
end;
% Построение графиков
figure(1);
plot(mass_t,mass_Um,'r',mass_t,mass_fc,'b');
grid on;
axis([0 5 0 250]);
figure(2);
k=0:K;
subplot(2,1,1);
plot(k*dt,v);
title('Скорость');
xlabel('t,с');
ylabel('v,м/с');
grid on;
subplot(2,1,2);
plot(k*dt,f);
title('Сила');
xlabel('t,с');
ylabel('F,Н');
grid on;
%end
Временные зависимости скорости и электромагнитного усилия синхронного явнополюсного линейного двигателя в режиме частотного пуска представлены на рис. 5.
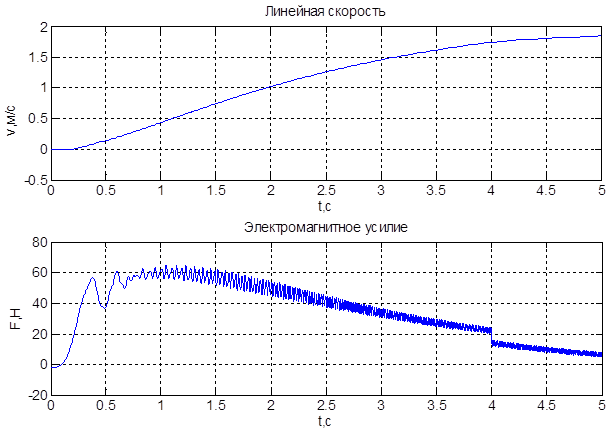
Рис. 5. Результат моделирования синхронного явнополюсного линейного двигателя в режиме частотного пуска с набросом нагрузки при t = 4 с
Зависимости токов 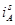 ,
, 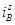 ,
, 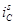 и
и  даны на рис. 6.
даны на рис. 6.
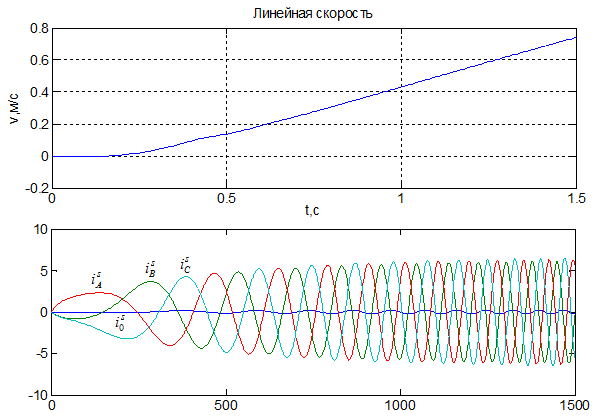
Рис. 6. Временные зависимости 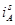 ,
, 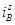 ,
, 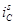 и
и 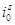 при k = 1500
при k = 1500
Литература:
1. Веселовский О.Н. и др. Линейные асинхронные двигатели / Веселовский О.Н., Коняев А.Ю., Сарапулов Ф.Н. – М.: Энергоатомиздат, 1991. – 256 с.
2. Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Боброва С.Д., Андреева Е.Д., Карлова М.В. Программирование синхронного явнополюсного дугостаторного двигателя (Z1 = 6) с трехфазной обмоткой индуктора с нулевым проводом. // Молодой ученый. – 2014. – №20 (79, декабрь). – С. 3-20.
3. Емельянов А.А., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф. Математическая модель синхронного неявнополюсного дугостаторного двигателя (Z1/Z2 = 6/12) с трехфазной обмоткой индуктора с нулевым проводом // Молодой ученый. – 2014. – №15 (74, сентябрь).
4. Емельянов А.А., Богатов Е.А., Клишин А.В., Медведев А.В., Симонович В.Г. Математическая модель линейного асинхронного двигателя на основе магнитных схем замещения // Молодой ученый. – 2010. - №5. – С. 14-22.
5. Емельянов А.А., Медведев А.В., Богатов Е.А., Кобзев А.В., Бочкарев Ю.П. Программирование линейного асинхронного двигателя в MATLAB // Молодой ученый. – 2013. - №3. – С. 129-143.
6. Емельянов А. А., Медведев А. В., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Иванин А.Ю. Программирование линейного асинхронного двигателя с числом пазов в индукторе равном шесть // Молодой ученый. – 2013. – № 10 – С. 23-38.
7. Емельянов А. А., Медведев А. В., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Иванин А.Ю. Моделирование линейного асинхронного двигателя с укладкой обмотки индуктора (Z1=6) через спинку ярма // Молодой ученый. – 2013. – № 10 – С. 39-54.
8. Емельянов А.А., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Бочкарев Ю.П., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Иванин А.Ю. Программирование линейного асинхронного двигателя (Z1 = 6) с трехфазной обмоткой индуктора с нулевым проводом // Молодой ученый. – 2014. – №2. – С. 36-51.
9. Емельянов А.А., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Габзалилов Э.Ф., Киряков Г.А. Моделирование системы АИН ШИМ — линейный асинхронный двигатель (Z1 = 6) с классическим типом обмотки с нулевым проводом // Молодой ученый. – 2014. – №6(65,май). – С. 24-43.
10. Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф. Программирование синхронного неявнополюсного дугостаторного двигателя (Z1 = 6) с трехфазной обмоткой индуктора с нулевым проводом // Молодой ученый. – 2014. – №16 (75, октябрь).-c. 19-39.
11. Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Киряков Г.А., Чернов М.В., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Боброва С.Д., Андреева Е.Д. Программирование синхронного неявнополюсного дугостаторного двигателя (Z1/Z2 = 12/24) с трехфазной обмоткой индуктора с нулевым проводом. // Молодой ученый. – 2014. – №18 (77, ноябрь). – С. 24-47.







