В данной статье ставится и решается задача о нахождении корней многочлена над булевым кольцом. Представлен алгоритм решения уравнений и систем уравнений от одной переменной над алгеброй множеств. А также рассмотрено применение изложенного материала при оценке мощности множества.
Ключевые слова: булево кольцо, булева алгебра, многочлен, алгебра множеств, мощность множества, кольцо многочленов
This article is formulated and solved the problem of finding the roots of a polynomial over a Boolean ring. An algorithm for solving equations and systems of equations in one variable over an algebra of sets. And also considered the use of the material in the assessment of the power set.
Keywords:Boolean ring, Boolean algebra, polynomial algebra of sets, cardinality, the ring of polynomials
Как известно, над любым коммутативным кольцом с единицей можно построить кольцо многочленов. В данной статье ставится и решается задача о нахождении корней многочлена над булевым кольцом. В частности рассматривается случай, когда носителем кольца является булеан. При нахождении корней многочлена применяется теорема, связывающая булево кольцо с соответствующей булевой алгеброй; на основе этой теоремы доказывается еще ряд предложений. Также будет представлен алгоритм решения уравнений и систем уравнений от одной переменной над алгеброй множеств, который вытекает из решения основной задачи. В конце статьи рассмотрено применение изложенного материала при оценке мощностей множеств.
Булевым кольцом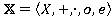
называется ассоциативное коммутативное кольцо с единицей
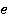, в котором все элементы идемпотентны, то есть 
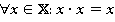. Причем бинарная операция сложения обладает следующим свойством: 
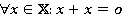,то есть каждый элемент является симметричным самому себе относительно операции сложения [1 c.75].
Рассмотрим булево кольцо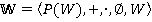 
, где 
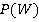— множество всех подмножеств некоторого множества 
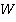(булеан). Операция сложения — симметрическая разность множеств (по определению 
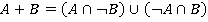, где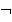 
— операция дополнения до множества 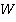), умножение — операция пересечения множеств. Кольцом многочленов
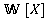, полученное присоединением к кольцу 
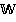переменной 
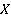, содержит многочлены вида 
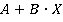, где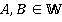 
.Вообще, данное кольцо содержит многочлены вида 
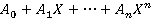, но так как кольцо идемпотентно, то 
.
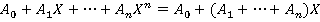Задача. Найти общее решение уравнения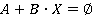 
над кольцом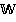, где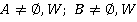 
.
Можно записать это уравнение иначе: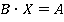 
(прибавить к обеим частям 
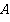). Так как кольцо 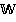не является полем и при этом оно имеет характеристику равную 2 (порядок единицы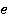в аддитивной группе кольца равен 2), то решить такое уравнение не так уж и просто.
Для решения поставленной задачи необходимо сформулировать ряд определений и предложений.
Булевой алгеброй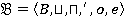 
называется множество 
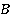, содержащее, по крайней мере, два элемента — нуль 
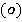и единица
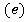, с заданным на нем некоторыми бинарными операциями 
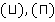и унарной операцией 
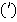. При этом для любых 
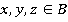выполняются следующие аксиомы булевой алгебры свойства:
1) 
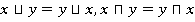— законы коммутативности
2) 
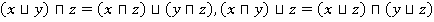— законы дистрибутивности
3) 
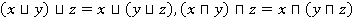— законы ассоциативности
4) 
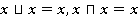— законы идемпотентности
5) 
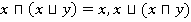— законы поглощения
6) 
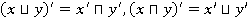— законы де Моргана
7) 
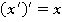— закон инволюции
8) 
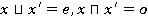— законы полноты и обособленности дополнения [2 с. 4].
Свойства:
1) 
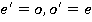
2) 
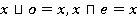
3) 
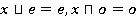[2].
Теорема. Всякая булева алгебра является булевым кольцом относительно операци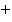й 
и 
, определенных равенствами: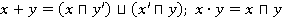
. При этом нуль и единица булева кольца совпадают с нулем и единицей булевой алгебры. Обратно, всякое булево кольцо является булевой алгеброй относительно операций 
, 
, 
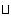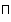, определенных равенствами: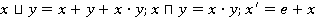 
[1 с.75].
На носителе булевой алгебры можно ввести некоторый частичный порядок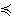 
(например, это может быть 
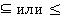, в зависимости от носителя), следующим образом: 
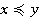тогда и только тогда, когда
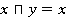[1]. Рассмотрим алгебру множеств 
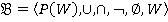. На носителе алгебры множеств можно ввести частичный порядок «включение»
.
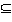Предложение 1. В булевой алгебре имеет место: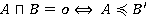 
, 
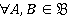
Доказательство.
Необходимость.
.
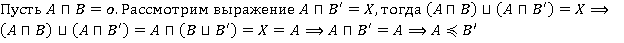Достаточность.
.
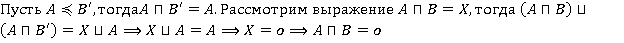На носителе булева кольца также можно ввести некоторый частичный порядок 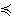следующим образом: 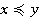тогда и только тогда, когда
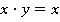[1]. Если рассмотреть булево кольцо
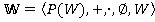, то на его носителе можно ввести частичный порядок «включение» .
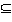Предложение 2. В булевом кольце имеет место: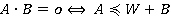 
, 
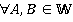
Доказательство. Вытекает из теоремы и предложения 1.
По теореме булево кольцо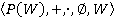 
является алгеброй множеств 
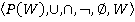, и наоборот.
Вернемся к основной задаче. В соответствии с теоремой можно уравнение 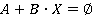преобразовать к виду 
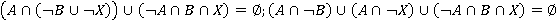. Далее, из законов алгебры множеств известно, что объединение совокупности множеств равно пустому множеству тогда и только тогда, когда каждое из множеств данной совокупности пустое, поэтому можно составить следующую систему: 
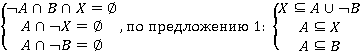. Таким образом, 
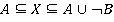, причем 
.
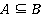В соответствии с теоремой, получим, что решение уравнения 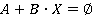имеет вид: 
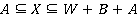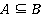, (действительно, 
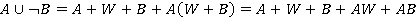, так как 
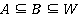, то очевидно, что 
, тогда 
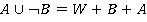). Таким образом, любой многочлен от одной переменной над булевым кольцом имеет такой вид решения.
Можно указать способ решения уравнений над алгеброй множеств. Пусть дано некоторое уравнение над алгеброй множеств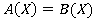
. Оно равносильно уравнению 
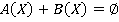. Далее, уравнение 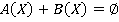необходимо привести к виду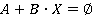, и тогда решение можно записать в следующем виде: 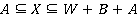, , 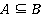или в виде:, .
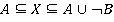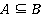Пример 1. Решить уравнение над алгеброй множеств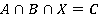
.
Применяя теорему, получим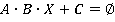 
. Тогда решение будет иметь вид 
, 
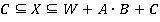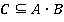. Можно данное решение записать и в следующем виде: 
.
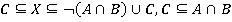Алгоритм получения решения уравнений над алгеброй множеств:
1) привести уравнение 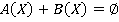к виду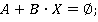 
2) записать решение в виде 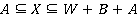, 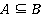или в виде , .
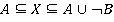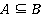Рассмотрим решение системы уравнений над алгеброй множеств.
Пусть дана система двух уравнений с одной переменной: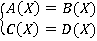 
Приводим каждое уравнение к виду 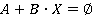и, решая каждое в отдельности, получим: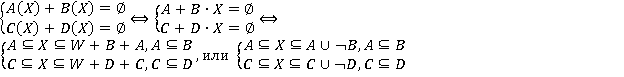 
Для нахождения общего решения системы сформулируемпредложение и докажем его.
Предложение 3.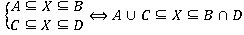
Доказательство.
Необходимость и достаточность («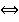
»):
.
Таким образом, на основании предложения3 заключаем, что общее решение системы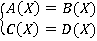имеет вид: 
, 
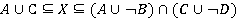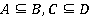, или: 
, .
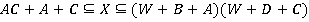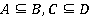Следствие.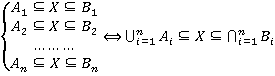 
Доказательство. На основании предложения 3.
Пример 2. Решить систему уравнений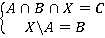 
.
Приводим обе системы к виду :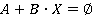
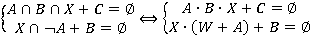.Далее запишем решение каждого из уравнения: 
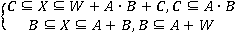. Тогда общее решение имеет вид: 
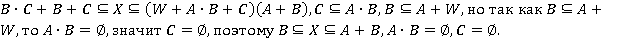Или: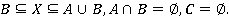 
Алгоритм получения решения системы уравнений над алгеброй множеств:
1) решить в отдельности каждое из уравнений системы, применяя алгоритм для одного уравнения;
2) найти общее решение, применяя предложение 3 или его следствие.
Рассмотрим булево кольцо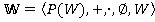, где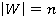
, тогда 
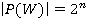. Пусть дано некоторое выражение 
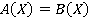. Приведем его к виду 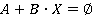, и пусть известны мощности множеств 
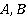. Задача состоит в оценке мощности множества .
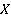Очевидно, что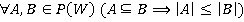 
, где .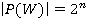 
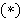
Для оценки мощности множества можно в некоторых случаях использовать формулу включения-исключения:
,
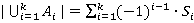где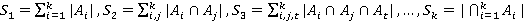 
[3].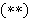
Решение уравнения 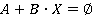имеет вид: 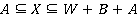, 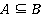. Тогда, на основании
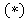, получаем следующую оценку для мощности множества
: 
, 
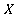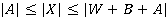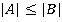. Можно ли упростить выражение 
?
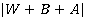Предложение 5.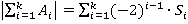 
Доказательство. Доказательство проведем методом математической индукции по числу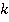
.
База индукции.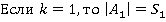 
. 
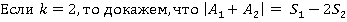. Построим диаграмму Эйлера-Венна в общем виде.
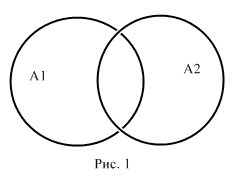
Из рисунка 1 видно, что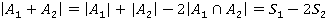 
.
Шаг индукции. Пусть предложение истинно для всех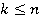 
. Докажем, что предложение имеет место для 
.
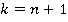Имеем, что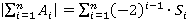 
. Тогда 
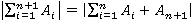. Из базы индукции известно, что 
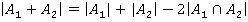, тогда 
.
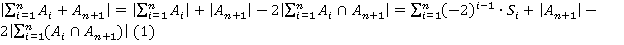Далее, преобразуем выражение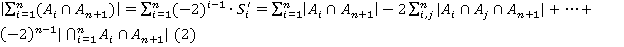 
.
В итоге, подставляя (2) в (1), получим: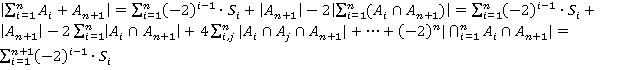 
.
Вывод индукции: предложение истинно для любых натуральных .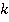
Таким образом, в соответствии с предложением 5,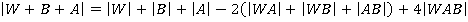 
. Так как 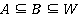, то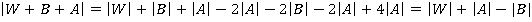 
.
Таким образом, оценка мощности множества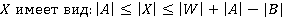 
, .
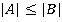Если множества 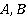представляют собой сложные выражения, то для вычисления их мощностей можно воспользоваться формулой включения-исключения
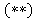, при этом необходимо знать мощности всевозможных пересечений простых множеств, составляющих сложные выражения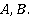 
Пример 3. Оценить мощность множества 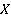, если известно, что 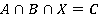, при этом 
.
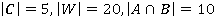Решение данного уравнения имеет вид 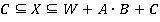, , 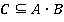тогда 
, 
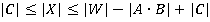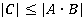. Таким образом, 
.
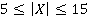Нетрудно заметить, что если построить кольцо многочленов от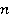 
переменных над булевым кольцом с тривиальным носителем 
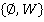(то есть над кольцом 
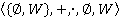), то полученное кольцо многочленов от 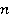переменных будет изоморфно кольцу многочленов от 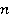переменных над 
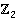(в силу изоморфизма колец 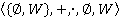и 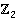, которые являются полями). Такое кольцо называют кольцом булевых многочленов (или полиномов Жегалкина).
Таким образом, в статье исследована одна из основных задач теории многочленов — нахождение корней многочленов над некоторым кольцом, в частности над булевым кольцом. Было показано, что, не смотря на свою кажущуюся простоту, уравнение вида 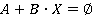над кольцом
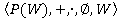, где 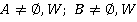, имеет не тривиальное решение в этом кольце. Это обусловлено необычными свойствами данного кольца (по сравнению, например, с кольцом целых чисел). Приведены алгоритмы решения данного уравнения и системы уравнений, основанные на теореме, связывающей булево кольцо с соответствующей булевой алгеброй. А также решена задача об оценке мощности множества, для которого задано уравнение 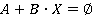над булевым кольцом с носителем конечной мощности. В дальнейшем планируется исследование многочленов в кольце
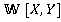, а также и в кольце 
.
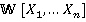Литература:
1. Владимиров Д. А. Булевы алгебры — М.: Наука, 1969. — 320 с.
2. Гуров С. И. Упорядоченные множества и универсальная алгебра (вводный курс). — М.: Издательский отдел ф-та ВМиК МГУ, 2005. — 83 с.
3. Елисеев Е. М., Елисеев М. Е. Элементы дискретной математики: Учебное пособие — Арзамас: АГПИ, 2003. — 98 с.
4. Куликов Л. Я. Алгебра и теория чисел: Учебное пособие для педагогических институтов — М.: Высшая школа, 1979. — 559 с.
5. Сангалова М. Е. Курс лекций по математической логике: Учебное пособие — Арзамас: АГПИ, 2006. — 98 с.
