В статье показано, как с помощью компьютерной модели интерференции волн от двух точечных источников, предлагаемой автором, обучающимся демонстрируют изменение интерференционной картины при изменении расстояния между источниками когерентных волн.
Ключевые слова:компьютерное моделирование, модель, учебная компьютерная модель, интерференция, когерентные волны, опыт Юнга, обучение физике.
Эта статья является продолжением наших статей, опубликованных ранее [1; 2; 3; 4; 7; 8; 10]. В ней также показано, как с помощью компьютерного моделирования можно визуализировать интерференционную картину, описываемую математическими соотношениями, для успешного изучения явления интерференции обучающимися [1; 2; 5, с. 13–18; 8].
В учебной теории интерференции волн от двух точечных источников приводится формула для расчета ширины максимумов интерференционной картины [1]:
Δx= xk+1 - xk= yλ / d,
где k — номер интерференционного максимума, y — расстояние от отрезка, соединяющего источники волн, до наблюдаемой картины распределения интенсивности вдоль прямой; λ — длина волн, испускаемых источниками; d — расстояние между этими источниками. Как правило, это выражение выводится в учебниках аналитическим способом, при этом считается, что y >> d. По этой причине на теоретическом графике зависимости интенсивности интерферируемой волны I(x) максимумы интенсивности имеют одинаковую ширину (рис. 1). Анализируя формулу, обучающиеся могут сделать вывод, согласно которому при приближении источников друг к другу (при неизменном расстоянии до линии, вдоль которой рассматривается распределение интенсивности) ширина интерференционных максимумов увеличивается (рис. 1). Если расстояние уменьшится в n раз, то ширина максимумов увеличится в n раз (в том приближении, о котором говорилось выше).
Если продемонстрировать обучающимся приведенную выше приближенную формулу для расчета ширины интерференционных максимумов и соответствующие ей графические иллюстрации, представленные на рис. 1, это не будет достаточным для формирования у обучающихся правильных и полных представлений о картине распределения интенсивности интерферируемой волны.
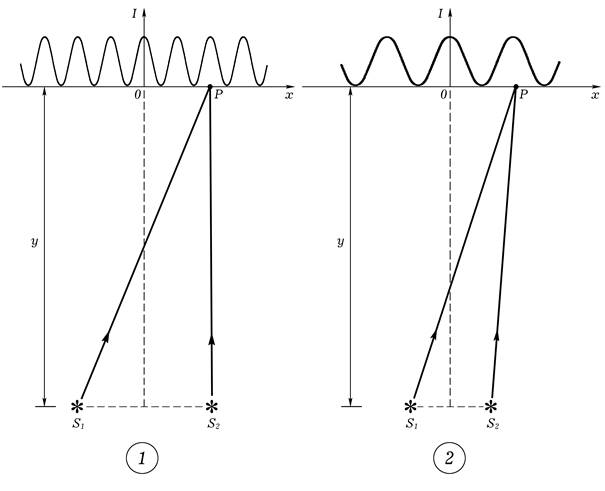
Рис. 1. Схема опыта Юнга, используемая для расчета приближенной интерференционной картины
Для того чтобы эти представления стали более полными, мы предлагаем использовать учебную компьютерную модель интерференции, достаточно подробное описание которой было приведено нами в предыдущих статьях [2; 3; 8]. Компьютерная программа, реализующая эту модель, демонстрирует обучающимся два вида распределения интенсивности интерферируемой волны: распределение вдоль отрезка прямой и распределение на плоскости (рис. 2). Первое представляет собой график зависимости I(x),второе распределение I(x, y) фактически представляет собой распределение интенсивности I на плоскости xOy, визуализированное с помощью следующего приема — каждому значению интенсивности в данной точке плоскости сопоставлены точки одного цвета, норазной яркости (чем больше значение, тем больше яркость).
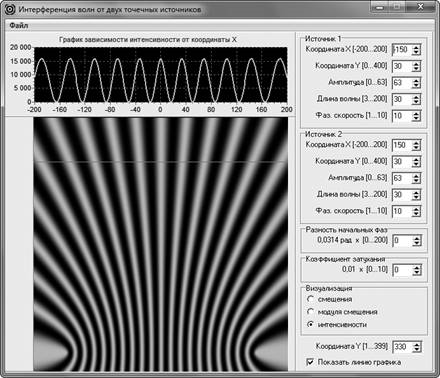
Рис. 2. Распределения интенсивности интерферируемой волны вдоль прямой и на плоскости
Программа позволяет осуществить визуализацию интерференционной картины и продемонстрировать изменение интерференционной картины при уменьшении (или увеличении) расстояния между источниками волн. Сначала обучающимся демонстрируется интерференционная картина, представленная на рис. 2, а затем — та, которая представлена на рис. 3. Анализировать результаты такого численного эксперимента значительно проще, чем результаты умозрительного эксперимента, который каждый из обучающихся должен провести, опираясь на фрагменты теории интерференции, о которых было сказано в начале этой статьи [6]. Кроме того, учащиеся видят, что максимумы не одинаковы по ширине. Картина распределения на плоскости позволяет говорить о том, что множества точек, соответствующие максимумам интенсивности, представляют собой двуполостные гиперболоиды вращения. Вряд ли преподавателю удастся об этом убедительно и доказательно рассказать, если он в своем рассуждении, предназначенном для обучающихся, будет опираться только на существенно упрощенную математическую модель, о которой говорилось в начале статьи. Отметим также, что учебный физический эксперимент, визуализирующий аналогичные рассмотренным картины распределений интенсивности при интерференции волн, довольно сложен в плане его постановки и получения наглядных экспериментальных результатов [9, с. 103–112; 10].
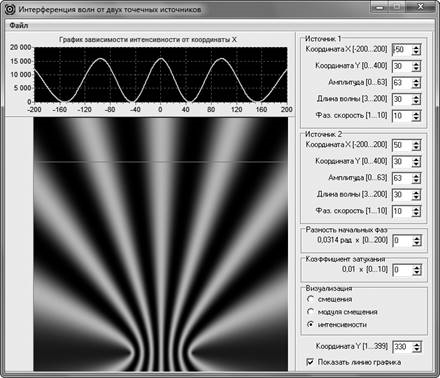
Рис. 3. Изменение вида распределений интенсивности интерферируемой волны вдоль прямой и на плоскости в случае приближения источников волн друг к другу
Литература:
1. Данилов О. Е. Демонстрация зависимости распределения интенсивности интерферируемой волны вдоль прямой от расстояния между этой прямой и отрезком, соединяющим точечные источники когерентных волн, с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 16. — С. 15–19.
2. Данилов О. Е. Демонстрация явления интерференции волн от двух точечных источников с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 13. — С. 5–10.
3. Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 9. — С. 50–58.
4. Данилов О. Е. Компьютерная модель интерференции от двух точечных источников / О. Е. Данилов // Информатика: проблемы, методология, технологии: Материалы XI Международной научно-практической конференции, Воронеж, 10–11 февраля 2011 г.: в 3 т. Т. 3. Школа-конференция «Информатика в образовании». — Воронеж: Издательско-полиграфический центр Воронежского государственного университета, 2011. — С. 87–89.
5. Данилов О. Е. Компьютерное моделирование: Волновое уравнение. Численные методы решения физических задач. Borland Pascal. Учебно-методическое пособие / О. Е. Данилов. — Глазов: ГГПИ, 2009. — 24 с.
6. Данилов О. Е. Применение имитационного моделирования механических взаимодействий при обучении физике / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2014. — № 5. — С. 97–103.
7. Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7. — С. 84–94.
8. Компьютерная модель интерференции / О. Е. Данилов. — Электрон. дан. — Сайты Google, 2011. — Режим доступа: https://sites.google.com/site/intercommod/. — Загл. с экрана.
9. Профессиональное образование: модернизационные аспекты: коллективная монография. В 9 т. Т. 4. / Р. М. Абдулгалимов, Н. А. Артеменко, С. В. Белоусов, Т, Е. Беньковская, О. М. Бородулина, О. Е. Данилов, С. И. Моднов, Т. К. Ивашковская, А. Г. Маланов, М. В. Пац, Н. В. Попова, Н. Е. Попова, Е. И. Черкашина; под ред. О. П. Чигишевой. — Ростов-н/Д: Издательство Международного исследовательского центра «Научное сотрудничество», 2014. — 267 с.
10. Danilov O. Particular didactic principles on the use of computer visualization of the fields of physical quantities in the educational process / O. Danilov // Young Scientist USA: Education. — Lulu, 2014. — P. 29–32.







