Математическое моделирование взрывного разложения энергетических материалов

Работа посвящена созданию пакета прикладных программ, позволяющего моделировать процесс взрывного разложения энергетических материалов. При моделировании процесса необходимо учитывать диффузию активных частиц и перенос энергии химической реакции в твердом теле, которые приводят к перераспределению концентраций реагентов в кристалле. Показано, что при расчете потоков реагентов дрейфовой составляющей можно пренебречь и учитывать только диффузионную составляющую переноса.

Ключевые слова: математическое моделирование, разностная схема, цепная модель реакции, взрывное разложение, энергетические материалы, азид серебра.

The aim of this article is to work out the application package, which allows to simulate the explosion decomposition process of the energetic materials. The program should take into account the active particles’ diffusion and the transport of energy of the decomposition reaction, these both cause redistribution of the reagents’ concentration in the crystal bulk. It was shown that during the calculation of the reagents’ flows one can take into account only the diffusion component and neglect of the drift component.

Keywords: simulation, difference scheme, chain reaction, explosive decomposition, energetic materials, silver azide.

Задачей математического моделирования физико-химических процессов является одновременное рассмотрение химических превращений и физических процессов, среди последних наибольшее значение имеют диффузия продуктов реакции и исходных веществ [1, c. 13, 2, c. 42], теплопроводность [3, c. 195, 4, c. 40, 5, c. 79], поглощение (выделение) и передача энергии [6, c. 127, 7, c. 686, 8, c. 69]. Исследование моделей физико-химических процессов способствует решению двух задач — выяснению механизма и выявлению роли физических процессов [9, c. 95, 10, c. 750]. Особенное значение это имеет для изучения кинетики и механизма экзотермических реакций по критическим условиям воспламенения [11, c. 341, 12, c. 55] и скоростям распространения взрывного разложения [13, c. 23, 14, c. 38, 15, c. 97]. Кроме того, такое исследование позволяет получить сведения о закономерностях переноса. Часто в этом случае методы математического моделирования позволяют получить значительно больше информации о поведении системы и механизмах, чем этого можно достичь в реальном эксперименте [16, c. 378, 17, c. 99]. Прикладной аспект проблемы определяется разработкой физико-химических основ теории оптических детонаторов на основе инициирующих и вторичных взрывчатых веществ [17, c. 99, 18, c. 7, 19, c. 631]. Целью работы является формулировка основных принципов моделирования физико-химических процессов и создание пакета прикладных программ, позволяющего моделировать процесс взрывного разложения энергетических материалов.

Основные принципы моделирования физико-химических процессов

Моделирование кинетики процесса включает в себя решение следующих основных задач:

-          построение математической модели;

-          составление краевой задачи;

-          выбор методов численного решения систем дифференциальных уравнений.

При моделировании сложных физико-химических процессов часто приходится использовать различные методы упрощения. Так, при моделировании процесса диффузии часто используют многочисленные аналогии, в первую очередь, с процессом теплопроводности. Поскольку процессы диффузии и теплопроводности описываются одинаковыми дифференциальными уравнениями, то можно воспользоваться уже готовыми решениями из теории теплопроводности. Основанное на аналогиях (физическое) моделирование хорошо тем, что, используя модель, мы можем сразу получить необходимые графические зависимости и, сравнив их с экспериментом, найти искомые параметры диффузии. Преимущество этого метода по сравнению с математическим моделированием особенно наглядно в случае сложных сред и процессов.

В качестве граничных условий при решении задач в настоящей работе использовали граничные условия третьего рода. В начальный момент времени t₀ концентрации реагентов (электронов и дырок) принимались постоянными и малыми (p ~10¹⁰ см^–3) относительно концентраций e. h. пар, реализуемых после поглощения инициирующего импульса (p ~ 10¹⁸ см^–3). Расчет прекращался после прохождения временной переменной интервала заданных значений.

Часто для решения системы дифференциальных уравнений, описывающей поведение системы, используют разностные методы. При этом система дифференциальных уравнений и граничные условия заменяются алгебраической системой конечно-разностных уравнений, решение которой дает приближенные значения решения исходной краевой задачи в узлах сетки. Такие системы сравнительно просто решаются численно обычными методами линейной алгебры.

Для решения систем уравнений в работе был использован встроенный решатель дифференциальных уравнений ode15s системы расчетов MatLab. Данный решатель использует методы Рунге-Кутта с переменным шагом по времени 1–5 порядка. Рассматриваемый класс методов имеет большое преимущество перед остальными, состоящее в том, что скорость счета слабо зависит от точности вычисления Якобиана системы, который может определяться численным дифференцированием. Эффективность пакета обусловлена удачными оценками погрешности интегрирования и тем обстоятельством, что Якобиан системы пересчитывается не на каждом шаге интегрирования. Детальное обоснование выбора решателя приведено в работе [20, c. 15].

Модель взрывного разложения азида серебра

Моделирование процесса взрывного разложения в азиде серебра осуществлялось на основе модели разветвленной твердофазной цепной реакции [20, c. 15, 21, c. 153], учитывающей диффузию носителей цепи и возможность передачи энергии химической реакции кристаллической решетке, приводящей к генерации e. h. пары в r_o — окрестности области протекания реакции. Математическая запись модели имеет вид [13, c. 23, 22, c. 130]:

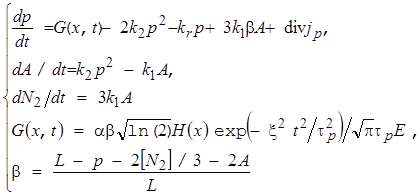                           (1)

где А — концентрация комплексов N₆, τ_p — длительность инициирующего импульса на полувысоте, Н (х) — распределение плотности энергии излучения на поверхности кристалла на расстоянии x от центра зоны облучения, L = 2·10²² см^-3 — число Лошмидта, β — доля невозбужденных узлов кристаллической решетки.

В общем случае поток дырок в (1) состоит из диффузионного и дрейфового членов:

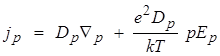                                                                               (2)

Так как внешнее поле (E_p) к кристаллу не прикладывается, дрейфовый член отличен от нуля лишь при появлении объемного заряда, характерный размер которого равен длине экранирования Дебая. При концентрациях электронных носителей заряда в момент инициирования р ~ 10¹⁸ см^-3 [23, с. 15] длина Дебая составляет:

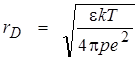 < 10 нм                                                                                      (3)

Время установления дрейфового равновесия 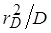 ~ 10 пс. По истечении этого времени диффузия проходит в амбиполярном режиме с коэффициентом, одинаковым для всех диффундирующих заряженных частиц [14, c. 38, 15, c. 97]:

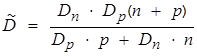,                                                                                    (4)

где D_n ≈ D_p — коэффициент диффузии электронов, n — концентрация электронов. Кроме того, в силу малости длины Дебая по сравнению с размерами образца и диаметром зоны облучения, а также быстротой установления дрейфового равновесия, можно пренебречь отклонением от электронейтральности. На стадии индукционного периода, развития и распространения реакции n > p, коэффициент амбиполярной диффузии .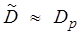

Аналитическая теория диффузии основана на дифференциальном уравнении Фика:

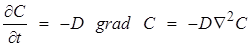,                                                                 (5)

где D — коэффициент диффузии, величина которого меняется в широких пределах: на десять порядков, от 10–⁴ до 10–¹⁴ м²/с. При моделировании коэффициент диффузии считался неизменным на всех этапах процесса. Отметим, что в общем случае, выбор системы координат, в которой осуществляется моделирование процесса зависит от симметрии эксперимента. Оператор Лапласа в декартовой системе координат имеет вид:

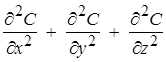                                                                                          (6)

Аппроксимируем дифференциальное уравнение диффузии с помощью разностного метода, основанного на приближенной замене производных отношениями приращений. Используем сетку с постоянным шагом, получив, таким образом, разбивку кристалла на kn ячеек (рис. 1). Необходимо перейти от уравнения (5) к соответствующему разностному уравнению, заменив лапласиан 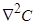 на его разностную аппроксимацию. Рассмотрим изменение количества частиц в n — ой ячейке, с учетом того, что концентрации частиц в ячейках (n-1), n, (n+1) неодинаковы и составляют C_(n-1), С_(n+1) соответственно:

Рис. 1. Одномерная сетка с постоянным шагом ∆x

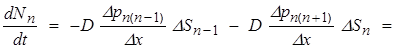
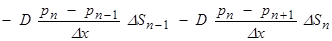                                                 (7)

где ∆x — шаг (размер ячейки), ∆S_n — площадь n — ой ячейки, p и N_n — концентрация и количество частиц в n — ой ячейке соответственно.

Перейдем от количества частиц к их концентрации:

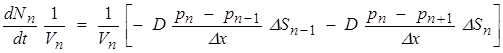
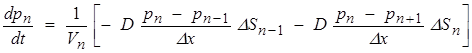              (8)

В том случае, когда кристалл симметричен, уравнение (6) будет иметь частный вид для крайних ячеек с номерами 1 и kn. Для последней ячейки поверхностная концентрация составляет бесконечно малую величину по сравнению с объемной, поскольку коэффициент рекомбинации на поверхности во много раз превышает аналогичную характеристику для объема. Полагаем, что кинетика рекомбинационного процесса на границе кристалла носит диффузионный характер.

При рассмотрении симметричного образца для уравнения изменения концентрации в первой ячейке необходим учет одного потока — на границе ячеек 1–2. Частный вид уравнения, отражающий изменение концентрации в первой ячейке:

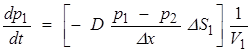                                                                        (11)

По аналогии можно записать уравнение, отражающее изменение концентрации в последней ячейке, учитывая, повышенную скорость рекомбинации частиц на поверхности образца:

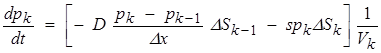,                                    (12)

где s — коэффициент поверхностной рекомбинации.

На основании уравнений (10–12), можно получить выражения для диффузии компонентов, учитывая, что ΔV_n= S_n Δx и что площадь сечения неизменна для любой рассматриваемой ячейки. В результате уравнения, отражающие изменение концентрации в ячейках n, k, 1, примут вид:

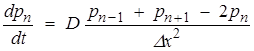,                                                                 (13)

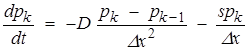,                                                                  (14)

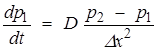.                                                                                         (15)

В декартовой системе координат объемы ячеек одинаковы на разном расстоянии от центра кристалла, следовательно, диффузия реагентов осуществляется между ячейками одинакового объема. Поэтому рассчитанные значения критической энергии инициирования и концентрации активных частиц меняются достаточно плавно.

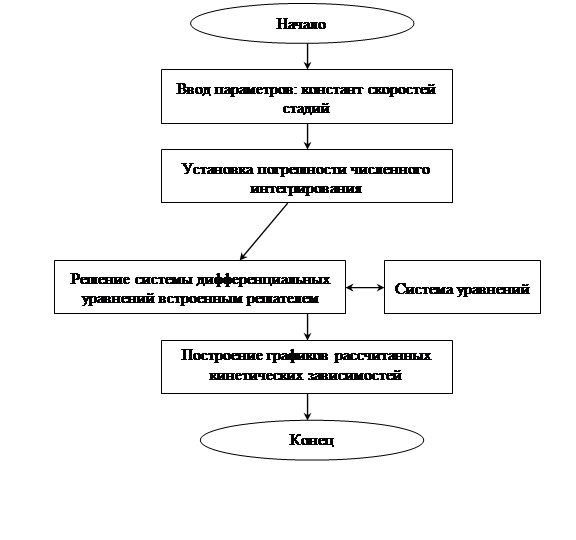
Для численного моделирования кинетических зависимостей концентраций реагентов в процессе разложения была создана программа в пакете MatLab (лицензия № 824977) создан пакет прикладных программа, блок-схема основных узлов которой приведена на рис. 2. Пакет прикладных программ позволяет решать следующие задачи:

-               рассчитывать кинетические закономерности разветвленных твердофазных цепных реакций;

-               представлять результаты расчетов в графическом виде и в виде числовых массивов;

-               сохранять полученные данные в файлы для их дальнейшего использования;

-               рассчитывать критические параметры инициирования взрывного разложения кристаллов энергетических материалов.

Функция задания правых частей системы обыкновенных дифференциальных уравнений (рис. 2) представлена ниже:

function dy = dekxA(t,y) %название функции

global kr k2 k1 kn x %передача глобальных констант пакета, одинаковых для всех программ. kr = 5·10⁶ с^-1 [24, c. 68], k2 = 4.5·10–¹² см³с^-1 [25, с. 10], k1= 2·10⁸ с^-1 [26, с. 45], kn =250 (количество ячеек), x = 5·10–⁶ см

dy = zeros(3*kn+1,1);             % a column vector

dy(1) = y(3*kn+1)*exp(-(5e7*t)^2) -2*k2*y(1)*y(1)+k1*(2e22-y(1)-2*y(2)-y(3))/2e22*3*y(2)-kr*y(1)+(y(4)-y(1))/2/x/x; %изменение концентрации дырок в первой ячейке

dy(2) = -k1*y(2)+k2*y(1)*y(1); %изменение концентрации переносчиков цепи в первой ячейке

dy(3) = 2*k1*y(2); %кинетика убыли анионов за счет химической реакции в первой ячейке

for n =2:1:kn-1 % цикл с параметром n определяет кинетику процесса в ячейках с номерами от 2 до 249 (предпоследней)

Рис. 2. Блок-схема программного комплекса расчета кинетики разветвленной твердофазной цепной реакции

dy(3*n-2) =y(3*kn+1)*exp(-(5e7*t))^2) -2*k2*y(3*n-2)*y(3*n-2)+k1*(2e22-y(3*n-2)-2*y(3*n-1)-y(3*n))/2e22*3*y(3*n-1)-kr*y(3*n-2)+(y(3*n+1)+y(3*n-5)-2*y(3*n-2)+0.5/(n-0.5)*(y(3*n+1)-y(3*n-5)))/4/x/x; % изменение концентрации дырок в ячейке с номером 3*n

dy(3*n-1) = -k1*y(3*n-1)+k2*y(3*n-2)*y(3*n-2); % изменение концентрации переносчиков цепи в в ячейках с номерами от 2 до 249

dy(3*n) =2*k1*y(3*n-1); % убыль анионов за счет химической реакции в текущей ячейке

end % окончание цикла

Результаты и выводы

Комплекс прикладных программ использован для моделирования взрывного разложения микрокристаллов азида серебра, инициированных импульсом неодимового лазера наносекундной длительности [27, с. 53]. Показано, что при размерах кристаллов меньше 10 мкм критическая плотность энергии инициирования взрывного разложения значительно возрастает, что позволяет использовать такие образцы в капсюлях оптических детонаторов. При моделировании химической реакции и расчете критических условий инициирования самоускоряющегося режима необходимо учитывать процессы переноса активных частиц и энергии химической реакции в твердом теле. В работе показано, что при расчете потоков реагентов (электронных возбуждений кристаллической решетки) дрейфовой составляющей можно пренебречь и учитывать только диффузионную составляющую переноса. Создан пакет прикладных программ, позволяющих рассчитывать кинетику процесса разложения и критические условия инициирования.

Литература:

1.         Ananyeva, M. V. Comparative analysis of energetic materials explosion chain and thermal mechanisms / M. V. Ananyeva, V. G. Kriger, A. V. Kalensii and others // Известия высших учебных заведений. Физика. — 2012. — Т.55. — № 11–3. — С. 13–17.

2.         Боровикова, А. П. Природа стадии обрыва цепи разветвленных твердофазных цепных реакций / А. П. Боровикова, М. В. Ананьева, О. В. Одинцова// Молодой ученый. — 2014. — № 15(74). — С. 41–45.

3.         Ананьева, М. В. Кинетические закономерности взрывного разложения ТЭНа, содержащего наноразмерные включения алюминия, кобальта и никеля / М. В. Ананьева, А. В. Каленский, Е. А. Гришаева и др. // Вестник КемГУ. — 2014. — № 1–1(57). — С. 194–200.

4.         Адуев, Б. П. Взрывчатое разложение ТЭНа с нанодобавками алюминия при воздействии импульсного лазерного излучения различной длины волны / Б. П. Адуев, Д. Р. Нурмухаметов, Р. И. Фурега и др. // Химическая физика. — 2013. — Т. 32. — № 8. — С. 39–42.

5.         Зыков, И. Ю. Критическая плотность энергии инициирования тэна с добавками наночастиц алюминия / И. Ю. Зыков // Международное научное издание Современные фундаментальные и прикладные исследования. — 2013. — № 1(8).– С. 79–84.

6.         Адуев, Б. П. Исследование оптических свойств наночастиц алюминия в тетранитропентаэритрите с использованием фотометрического шара / Б. П. Адуев, Д. Р. Нурмухаметов, Г. М. Белокуров и др. // Журнал технической физики. — 2014. — Т. 84. — № 9. — С. 126–131.

7.         Zvekov, A. A. Regularities of light diffusion in the compo site material pentaery thriol tetranitrate — nickel / A. A. Zvekov, M. V. Ananyeva, A. V. Kalenskii and others // Наносистемы: физика, химия, математика. — 2014. — Т. 5. — № 5. — С. 685–691.

8.         Никитин, А. П. Расчет критических параметров инициирования теплового взрыва тэна с наночастицами меди на разных длинах волн / А. П. Никитин // Международное научное издание Современные фундаментальные и прикладные исследования.– 2013. — № 4(11).– С. 68–75.

9.         Газенаур, Н. В. Зависимость показателя поглощения меди от длины волны / Н. В. Газенаур, И. Ю. Зыков, А. В. Каленский // Аспирант. –2014. — № 5. — С. 94–98.

10.     Звеков, А. А. Моделирование распределения интенсивности в прозрачной среде с Френелевскими границами, содержащей наночастицы алюминия / А. А. Звеков, А. В. Каленский, А. П. Никитин и др.// Компьютерная оптика. — 2014. — Т. 38. — № 4. — С. 749–756.

11.     Каленский, А. В. Спектральная зависимость критической плотности энергии инициирования композитов на основе пентаэритриттетранитрата с наночастицами никеля / А. В. Каленский, М. В. Ананьева, А. А. Звеков и др.// Фундаментальные проблемы современного материаловедения. — 2014. — Т. 11. — № 3. — С. 340–345.

12.     Кригер, В. Г. Влияние эффективности поглощения лазерного излучения на температуру разогрева включения в прозрачных средах / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др.// Физика горения и взрыва. — 2012. — Т. 48. –№ 6. — С. 54–58.

13.     Кригер, В. Г. Определение пространственных характеристик волны цепной реакции в азиде серебра / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Химическая физика. — 2014. — Т. 33. — № 8. — С. 22–29.

14.     Боровикова, А. П. Пространственно-временные характеристики волны горения в азиде серебра / А. П. Боровикова, А. В. Каленский, И. Ю. Зыков // Аспирант. — 2014. — № 3. — С. 37–42.

15.     Боровикова, А. П. Методика моделирования распространения взрывного разложения азида серебра / А. П. Боровикова, А. В. Каленский// Аспирант. — 2014. — № 4. — С. 96–100.

16.     Кригер, В. Г. Процессы теплопереноса при лазерном разогреве включений в инертной матрице / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Теплофизика и аэромеханика. — 2013. — Т. 20. — № 3. — С. 375–382.

17.     Каленский, А. В. Влияние длины волны лазерного излучения на критическую плотность энергии инициирования энергетических материалов / А. В. Каленский, А. А. Звеков, М. В. Ананьева и др. // Физика горения и взрыва. –2014. — Т. 50. — № 3. — С. 98–104.

18.     Ананьева, М. В. Перспективные составы для капсюля оптического детонатора / М. В. Ананьева, А. А. Звеков, И. Ю. Зыков и др. // Перспективные материалы. — 2014. — № 7. — С. 5–12.

19.     Kalenskii, A. V. The Microcenter Heat Explosion Model Modernization / A. V. Kalenskii, V. G. Kriger, A. A. Zvekov and others // Известия ВУЗов. Физика. — 2012. — Т. 55. — № 11–3. — С. 62–66.

20.     Кригер, В. Г. Механизм твердофазной цепной реакции/ В. Г. Кригер, А. В. Каленский, Ю. А. Захаров, В. П. Ципилев // Материаловедение. — 2006. — № 9. — С. 14–21.

21.     Кригер, В. Г. Инициирование азидов тяжелых металлов импульсным излучением / В. Г. Кригер, А. В. Каленский // Химическая физика. — 1995. — Т. 14. — № 4. — С. 152 - 160.

22.     Кригер, В. Г. Определение ширины фронта волны реакции взрывного разложения азида серебра / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Физика горения и взрыва. — 2012. — Т.48. — № 4. — С. 129–136.

23.     Каленский, А. В. Коэффициент захвата электронных носителей заряда на экранированном отталкивающем центре/ А. В. Каленский, М. В. Ананьева, В. Г. Кригер, А. А. Звеков // Химическая физика. — 2014. — Т. 33. — № 4. — С. 11–16.

24.     Кригер, В. Г. Диффузионная модель разветвленной цепной реакции взрывного разложения азидов тяжелых металлов / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Химическая физика. — 2009. — Т. 28. — № 8. — С. 67–71.

25.     Кригер, В. Г. Релаксация электронно-возбужденных продуктов твердофазной реакции в кристаллической решетке / В. Г. Кригер, А. В. Каленский, А. А. Звеков // Химическая физика. — 2012. — Т. 31. — № 1. — С. 18 - 22.

26.     Гришаева, Е. А. Неизотермическая модель разветвленной цепной реакции взрывного разложения энергетических материалов / Е. А. Гришаева, А. В. Каленский, М. В. Ананьева, А. А. Звеков// Фундаментальные проблемы современного материаловедения. — 2013. — Т. 10. — № 1. — С. 44–49.

27.     Ананьева, М. В. Инициирование взрывного разложения микрокристаллов азида серебра / М. В. Ананьева, А. В. Каленский // Молодой ученый. — 2014. — № 19. — С. 52–55.