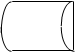
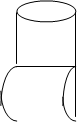
В данной статье представлены опыты с бутылкой Клейна. Поставлена проблема и решена экспериментально, прогнозирования экспериментов с разрезанием модели бутылки Клейна. Были выявлены ее свойства.
Ключевые слова: бутылка Клейна, лист Мебиуса, трехмерное пространство, топологическая поверхность.
Abstract. The article presents a series of experiments with the Klein bottle. Solves the problem of forecasting the result of the experiment with cutting the Klein bottle. We have also identified its properties.
Keywords: The Klein bottle, the Möbius strip, a three-dimensional space, topological surface.
Бутылка Клейна была описана немецким ученым Ф. Клейном в 1882 году.
С бутылкой Клейна знакомятся в высших учебных заведениях в курсе геометрии. Эта модель интересна тем, что ее свойства нельзя увидеть без проведения опытов, так как она не может существовать в нашем трехмерном пространстве. Модели, которые мы видим в магазинах, как сувенир имеют отдаленное представление о бутылки Клейна. Интересна возможность выявления свойств бутылки Клейна с помощью экспериментов.
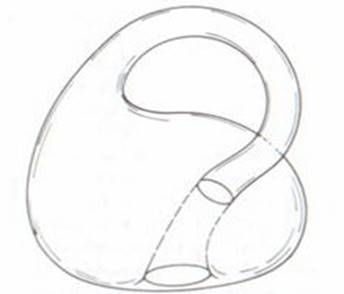
Рис.1. Бутылка Клейна
Бутылка Клейна – это неориентируемая определённая поверхность [1, с. 352]. Она частично связана с лентой Мёбиуса (прямоугольная лента, полученная склеиванием противоположных сторон с поворотом на 180 градусов [3]) и проективной плоскостью.
Изготовление бутылки Клейна





















 А
А
 |
 |
||||
 |
|||||
а) б) в)
Рис. 2. Изготовление бутылки Клейна
Сложите квадрат пополам и соедините его стороны, обозначенные пунктиром на рис.1 а). Сделайте прорезь на обращенной к вам половине квадрата, перпендикулярно склеенным сторонам рис.1 б). Между верхним краем и прорезью трубки должно быть расстояние равное четверти стороны квадрата. Перегнув модель пополам вдоль прямой А, протащите нижний край трубки сквозь прорезь, верхнее и нижнее основания трубки склейте друг с другом в соответствии со стрелками рис.1 в).
Видим, что склеить бутылку Клейна довольно сложно. Из прозрачного материала эта модель будет более наглядной. Далее проведем ряд экспериментов с бутылкой Клейна, описанных в таблице 1.
Вначале будут сделаны предположения, какой будет результат, затем проводится проверка высказанных нами предположений.
Таблица 1
Разрезание бутылки Клейна
|
№ п/п |
Эксперимент |
Предполагаемый результат |
Наблюдаемый результат |
|||
|
1 1 1 1 |
|
Зеркальные листы Мебиуса |
Высказанное предположение подтвердилось. |
|||
|
2
2 2 |
|
Лист Мебиуса
|
Высказанное предположение подтвердилось. |
|||
|
3
3 3 |
|
Три листа Мебиуса
|
В результате мы получили два листа Мебиуса и цилиндр. |
Описание опытов:
1. Склеили Бутылку Клейна и выполнили разрез посередине. Перед этим было высказано предположение, что результатом будет два листа Мебиуса. Данное высказывание подтвердилось.
2. Склеили бутылку Клейна, выполнили разрез по краю. Перед этим было высказано предположение, что получиться лист Мебиуса. Данное высказывание подтвердилось.
3. Склеили модель, выполнили два разреза по краям. Перед этим было высказано предположение, что результатом станет три листа Мебиуса. Высказанное предположение не подтвердилось. В результате были получены 2 листа Мебиуса и цилиндр.
Из проведенных нами опытов можно выделить следующие свойства бутылки Клейна:
1. Число сторон – 1.
2. Число Бетти – это число разрезов, которые можно провести так, чтобы поверхность не распалась на два отдельных куска [2, с. 507]. Так как бутылка Клейна не имеет краев (то есть поверхность замкнутая), то каждый разрез должен иметь форму какой-нибудь простой замкнутой кривой, поэтому число Бетти для нашей модели равно 2.
3. Хроматическое число (минимальное число цветов, в которые можно раскрасить модель так, чтобы концы любого ребра имели разные цвета) [5, с. 74]. Хроматическое число бутылки Клейна равно шести. Это означает, что на данной поверхности можно так расположить 6 областей разных цветов, чтобы 5 областей имели общие границы с шестой областью.
4. Бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием [6, с. 208]. Она, в отличие от листа Мёбиуса, является замкнутым многообразием, то есть компактным многообразием без края.
5. Она не может быть вложена в трёхмерное евклидово пространство Е3 (только погружена), но вкладывается в Е4.
6. Бутылка Клейна может быть получена склеиванием по краю двух лент Мёбиуса. Но в обычном трехмерном евклидовом пространстве Е3 сделать это невозможно, не создав самопересечения.
Выполняя опыты, мы наблюдали затем, что происходит с бутылкой Клейна и делали правильные предположения. В то время как изначально наши предположения могли быть неверными. Значит, именно проведенные нами опыты делают свойства построенной поверхности более доступными для понимания.
В результате проведенных опытов, мы убедились, что действительно бутылка Клейна не может существовать в трехмерном пространстве, а лишь в четырехмерном. В наше время её можно встретить в магазинах, в рекламе, а также в шоу фокусников (иллюзионист, забравшись в бутылку, остается на половину погруженным в нее) [4, с. 28]. Изготовить бутылку Клейна из стекла достаточно сложно, поэтому она имеет высокую стоимость и применяется крайне редко.
Литература:
1. Атанасян Л.С., Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. инс-ов. Ч-2. – М.: Просвещение, 1987. – 352 с.
2. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971. – 507 с.
3. Марушина Т.Д. Разрезание лент // Исследования в области естественных наук. 2014. № 7 [Электронный ресурс]. URL: http://science.snauka.ru/2014/07/7567 (дата обращения: 09.08.2014).
4. Пономарева Е.И., Первушкина Е.А. Развитие креативности школьников при обучение математике в 5-6 классах с использованием интерактивных геометрических средств // Перспективы науки. – 2011. – № 16. – С. 27-34.
5. Сангалова М.Е. Использование эксперимента при изучении топологических свойств поверхностей // Сборник научных трудов Sworld. – 2011. – Т. 23. – № 1. – С. 73 - 77.
6. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. – М.: МИРОС.КПЦ «Марта», 1992. – 208 с.