Метод естественной кластеризации данных

1. Введение

Задачей кластеризации является разбиение заданной выборки объектов на подмножества (кластеры) таким образом, чтобы каждый кластер содержал схожие объекты, а объекты разных кластеров как можно сильнее отличались друг от друга. В настоящее время существует большее количество разнообразных методов кластерного анализа. В большинстве методов отнесение объектов к одним классам, как правило, осуществляется на основании некоторой меры схожести, выраженной в виде расстояния между объектами в многомерном метрическом пространстве. Однако использование различных метрик, особенно таких распространенных как евклидово расстояние, степенное расстояние и т. д., может приводить к некорректным результатам в случае, если объекты содержат признаки различной природы, выраженные в разных шкалах или разных единицах измерения. Кроме того, такой подход не учитывает самого главного — внутренних взаимосвязей между объектами и их признаками, выраженных в виде внутренних законов, которым подчиняются объекты, и которые несут в себе истинную причину, определяющую схожесть объектов.

В работах [1,2] был предложен альтернативный подход, названный «естественной классификацией», суть которого заключается в том, что разбиение объектов на классы должно производиться в соответствии с закономерностями, которым удовлетворяют объекты. Это означает, что объекты одного класса должны подчиняться одной группе закономерностей, а объекты разных классов — разным группам закономерностей. Объекты одного класса также должны обладать некоторой целостностью, под которой понимается взаимная согласованность закономерностей каждой группы по взаимопредсказанию свойств объектов.

В данной работе предлагается использовать идеи метода естественной классификации для того, чтобы улучшить качество кластеризации популярных методов кластеризации на примере метода k-means. По аналогии с естественной классификацией предложенный методы был назван «естественной кластеризацией».

2. Метод естественной кластеризации

Метод естественной кластеризации можно разбить на следующие этапы:

-                   определение множества отношений, описывающих признаки объектов на языке логики первого порядка;

-                   обнаружение закономерностей;

-                   построение вероятностных описаний объектов;

-                   кластеризация.

Рассмотрим все перечисленные этапы.

Определение множества отношений, описывающих признаки объектов на языке логики первого порядка. Первым этапом метода является формализация различных признаков объектов и отношений между ними, важных с точки зрения эксперта, в языке логики первого порядка. Результатом формализации будет являться некоторый набор логических предикатов 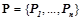. В качестве примера подобной формализации можно привести предикаты, описывающие равенство признаков определенным значениям, попадание признаков в интервал значений, сравнение значений признаков между собой и др. Отметим, что для решения более сложных задач могут быть использованы более сложные предикаты и классы гипотез [3,4]. В работе [3] описан общий способ задания различных классов гипотез для задач обнаружения закономерностей в таблицах данных.

Обнаружение закономерностей. После определения множества отношений осуществляется поиск закономерностей в терминах заданного набора предикатов. Алгоритм поиска вероятностных закономерностей основан на методологии семантического вероятностного вывода [5]. Отличительной особенностью семантического вероятностного вывода является использование понятия вероятностной закономерности, которое звучит следующим образом.

Вероятностной закономерностью называется правило 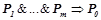, удовлетворяющее следующим условиям:

1)                 условная вероятность 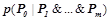 правила определена, т. е. ;

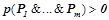2)                 условная вероятность 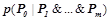 правила строго больше условных вероятностей каждого из его подправил, т. е. для любого правила 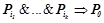, такого что 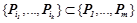, условная вероятность .

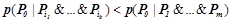Семантический вероятностный вывод позволяет находить все статистически значимые вероятностные закономерности вида .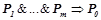

Для дальнейшего описания введем несколько определений.

Длиной правила 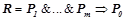 будем называть величину 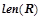, равную количеству предикатов, входящих в посылку правила.

Правило 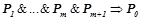 является уточнением правила 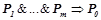, если оно получено добавлением в посылку правила  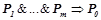произвольного предиката .

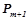Будем обозначать 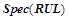 множество уточнений всех правил из 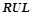, где 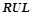 — произвольное множество правил вида , .

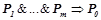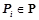Опишем алгоритм поиска закономерностей вида 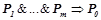 для некоторого выбранного целевого предиката .

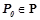На первом шаге генерируем множество 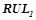 всех правил единичной длины, имеющих вид 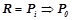, , 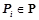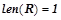. Все правила из  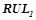проходят проверку на выполнение условий для вероятностных закономерностей 1) и 2). Правила, прошедшие проверку, будут являться вероятностными закономерностями. Обозначим  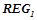множество всех вероятностных закономерностей, обнаруженных на первом шаге, т. 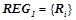е. , где 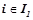, , 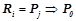, , 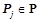 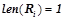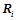— вероятностная закономерность.

На шаге 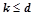 генерируется множество  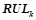всех уточнений правил, сгенерированных на предыдущем шаге, 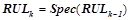. Все правила из  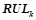проходят проверку на выполнение условий для вероятностных закономерностей 1) и 2). Обозначим  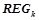множество всех вероятностных закономерностей, обнаруженных на данном шаге, т. 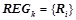е. , где 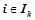, , 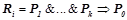, , 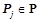 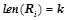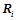— вероятностная закономерность.

На шаге 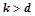 генерируется множество  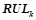всех уточнений всех вероятностных закономерностей, обнаруженных на предыдущем шаге, 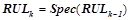. Все правила из  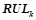проходят проверку на выполнение условий для вероятностных закономерностей. Обозначим  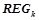множество всех вероятностных закономерностей, обнаруженных на данном шаге, т. 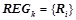е. , где 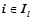, , 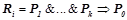, , 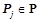 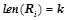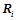— вероятностная закономерность.

Алгоритм останавливается, когда невозможно далее уточнить ни одно правило, т. е. когда 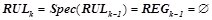. Результирующее множество всех закономерностей 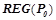, предсказывающих целевой предикат 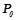, будет равно объединению всех : .

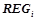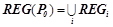Шаги алгоритма 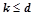 называются базовым перебором, а шаги  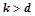— дополнительным перебором. Величина  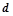называется глубиной базового перебора и является параметром алгоритма. В практических задачах глубина базового перебора обычно берется равной двум или трем.

Чтобы проверить при помощи обучающего множества, является ли некоторое правило 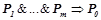 вероятностной закономерностью, необходимо проверить выполнимость вероятностных неравенств 1) и 2), и оценить его статистическую значимость.

Условная вероятность правил при выполнении алгоритма оценивается при помощи обучающего множества. Для того чтобы избежать генерации статистически незначимых правил, на практике обычно вводятся различные дополнительные критерии, оценивающие статистическую значимость. Правила, не удовлетворяющие этим критериям, отсеиваются, даже если они имеет высокую точность на обучающем множестве.

Для нахождения множества всех закономерностей  последовательно берется каждый предикат из 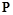 в качестве целевого и при помощи описанного алгоритма находится множество предсказывающих его закономерностей. Таким образом, множество всех закономерностей .

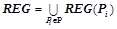Построение вероятностных описаний объектов. Следующим этапом естественной кластеризации является воссоздание вероятностных описаний объектов. При построении вероятностных описаний объектов мы основываемся на том, что характерные для объектов признаки должны быть связаны между собой взаимным предсказанием, тогда как случайные признаки таких связей не должны иметь. Процедура построения сводится к тому, что мы, используя закономерности, создаем новое описание объекта, составленное из вероятностных оценок наличия признаков, которые предсказываются по имеющемуся набору признаков реального объекта. Таким образом, в подобном вероятностном описании характерные для объекта признаки будут иметь высокие оценки, тогда как случайные признаки — низкие или нулевые.

Обозначим 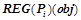 — множество закономерностей из , предсказывающих предикат 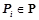 и применимых к объекту 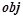. Т. е. 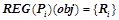, где 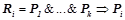, таких, что предикаты  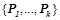принимают значение «истина» на объекте .

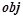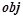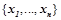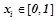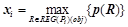Вероятностным описанием объекта  будем называть набор , , где , где 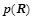 — условная вероятность правила 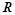. Т.е вероятностным описанием будет являться набор вещественных чисел 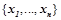, где каждое значение  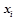представляет собой максимальную вероятность, с которой закономерности из  предсказывают предикат 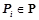 на объекте .

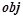Полученное таким образом описание, во-первых, будет включать все характерные для данного объекта признаки, поскольку такие признаки будут предсказываться закономерностями, во-вторых, не будет содержать случайных признаков, поскольку для таких признаков будут отсутствовать предсказывающие закономерности, и, в-третьих, будет показывать вероятность, с которой каждый признак может присутствовать в описании объекта.

Отметим также, что использование вероятностных описаний вместо исходных объектов позволяет более корректно применять различные метрики расстояний при вычислении близости между объектами, поскольку все координаты вероятностных описаний имеют одинаковые единицы измерения.

Кластеризация. Заключительным этапом является кластеризация полученных вероятностных описаний объектов. Для этих целей можно использовать различные существующие алгоритмы, однако в данной работе было решено остановиться на широко распространенном методе k-means [6]. Данный алгоритм позволяет разделить множество данных на заданное пользователем число кластеров таким образом, чтобы минимизировать расстояние между объектами кластеров до центров этих кластеров.

Поскольку алгоритм хорошо представлен в литературе, приведем только основные этапы его работы.

1.                  Выбрать начальное приближение центров всех кластеров.

2.      Отнести каждый объект выборки к ближайшему центру в соответствии с выбранной метрикой.

3.      Пересчитать центры кластеров как центры масс всех точек, входящих в соответствующие кластеры.

4.      Повторять шаги 2, 3 пока центры кластеров не перестанут изменяться.

Поскольку алгоритм k-means очень чувствителен к выбору начальных приближений центров классов, то на практике часто стараются выбрать начальные точки так, чтобы они были максимально удалены друг от друга.

В описанных ниже экспериментах была использована модификация алгоритма k-means, известная под названием k-medoids [7]. Отличие заключается в том, что на шаге 3 в качестве центра кластера вместо центра масса выбирается конкретный объект кластера, для которого сумма расстояний до всех остальных объектов кластера минимальна. В качестве метрики использовалась так называемая «манхэттенская метрика», в которой расстояние между объектами определяется как сумма модулей разностей значений их признаков.

3. Эксперименты с искусственными данными

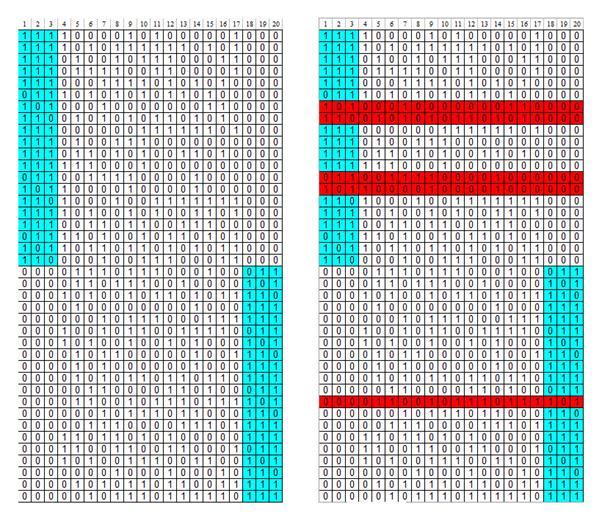
Рис. 1. Таблица с искусственными данными. Слева — исходная таблица. Справа — результаты кластеризации стандартного метода k-means

 

Проведем сравнение работы предложенного метода со стандартным методом k-means на примере решения следующей тестовой задачи. Дана таблица (рис. 1), в которой представлены 40 объектов (строки таблицы). Каждый объект описывается 20-ю бинарными признаками (столбцы таблицы). Все объекты разбиты на 2 очевидных класса: первый класс — строки с 1 по 20, которые содержат преимущественно «1» в столбцах 1–3 и «0» в столбцах 18–20, второй класс — строки с 21 по 40, содержащие преимущественно «1» в столбцах 18–20 и «0» в столбцах 1–3. Остальные столбцы с номерами 4–17 у всех строк содержат случайный шум. Таким образом, таблица данных характеризуется тем, что, во-первых, в ней отсутствует какой-либо один-единственный признак, которого было бы достаточно для однозначной классификации, а во вторых, большая часть признаков (70 % всех признаков) содержат случайную информацию. Задача состоит в том, чтобы разбить все объекты на 2 класса. Качество кластеризации будет оцениваться по тому, насколько полученные кластеры совпадут с реальными классами, встроенными в таблицу.

Результат кластеризации стандартным методом k-means показан на рисунке 1 справа. На рисунке выделены 5 строк, которые были неправильно классифицированы. Таким образом, совпадение классов составляет 87.5 %.

Результат работы предложенного метода естественной кластеризации показал 100 %-е совпадение классов. Благодаря тому, что методом были обнаружены закономерности, связывающие все значимые для классификации признаки, были построены вероятностные описания объектов, которые содержали высокие оценки только для информативных признаков (столбцы 1–3 и 18–20) тогда как для случайных признаков (столбцы 4–17) оценки были нулевые, поскольку отсутствовали предсказывающие их закономерности. Полученные таким образом вероятностные описания объектов уже легко и безошибочно разбивались на 2 класса.

4. Применение в медицинской диагностике

Предложенный метод естественной кластеризации был использован для решения задачи автоматической классификации фолликулярного рака и фолликулярной аденомы щитовидной железы. В настоящее время в вопросах дооперационной диагностики заболеваний щитовидной железы наибольшие трудности вызывает диагностика фолликулярной опухоли при попытке отличить аденому от рака. Как показывает опыт, в настоящее время совпадение цитологических и окончательных гистологических диагнозов не превышает 56 % [8]. Таким образом, встает вопрос о совершенствовании дооперационной морфологической диагностики.

Исходные данные для исследования были предоставлены цитологической лабораторией Дорожной клинической больницы Новосибирска. Данные содержали цитологические препараты 170 больных с уже известными диагнозами (70 случаев рака и 100 случаев аденомы), проанализированные по 30-и цитологическим признакам и представлены в виде таблицы. Задачей исследования является автоматическая кластеризация цитологических препаратов на 2 класса и оценка совпадения полученных классов с диагнозами этих препаратов (рак или аденома).

В соответствии с описанным выше методом из таблицы данных были извлечены закономерности, связывающие цитологические признаки по взаимному предсказанию, построены вероятностные описания объектов и проведено разбиение на 2 класса. Результаты показали, что совпадение полученных классов с диагнозами составило 94.7 %. Только у 9 препаратов из 170 принадлежность к классу не совпала с диагнозом.

Для сравнения также была проведена кластеризация препаратов стандартным методом k-means, результаты которого показали совпадение классов с диагнозами на 82.4 %. У 30 препаратов из 170 класс не совпал с диагнозом.

Таким образом, проведенное сравнение показывает, что качество кластеризации у предложенного метода значительно выше, чем у распространенного метода k-means. Кроме того, полученная высокая степень совпадения классов с диагнозами (94.7 %) позволяет сделать вывод о возможности использования предложенного метода для повышения качества дооперационной диагностики.

5. Заключение

Проведенные эксперименты показывают преимущество предложенного метода естественной кластеризации по сравнению с известным методом k-means. Кроме того, необходимо отметить, что помимо разбиения анализируемого множества данных на кластеры предложенный метод также дает и множество закономерностей, которым подчиняются объекты. Эти закономерности могут быть использованы для предсказания признаков объектов, прогнозирования новых объектов, восстановления искаженных признаков объектов, фильтрации шумов, а также для исследования самой природы связей между объектами.

6. Благодарности

Данные цитологического исследования препаратов больных подготовила и предоставила д. м.н. Полоз Т. Л. .

 

Литература:

 

1.      Витяев Е. Е., Морозова Н. С., Сутягин А. С., Лапардин К. А. Естественная классификация и систематика как законы природы // Анализ структурных закономерностей. — Новосибирск, 2005. — Вып. 174: Вычислительные системы. — С. 80–92.

2.      Демин А. В., Витяев Е. Е. Метод построения «естественной» классификации // Информационные технологии в гуманитарных исследованиях. — Новосибирск: ИАЭТ СО РАН, 2010. — Вып. 15. — С. 16–22.

3.      Демин А. В., Витяев Е. Е. Разработка универсальной системы извлечения знаний «Discovery» и ее применение // Вестник НГУ, серия: Информационные технологии. — 2009. — Т. 7. — Вып. 1. — С. 73–83.

4.      Демин А. В., Витяев Е. Е. Реализация универсальной системы извлечения знаний «Discovery» и ее применение в задачах финансового прогнозирования // Информационные технологии работы со знаниями: обнаружение, поиск, управление. — Новосибирск, 2008. — Вып. 175: Вычислительные системы. — С. 3–47.

5.      Витяев Е. Е. Извлечение знаний из данных. Компьютерное познание. Модели когнитивных процессов. — Новосибирск: НГУ, 2006. — 293 с.

6.      MacQueen J. Some methods for classification and analysis of multivariate observations // In Proc. 5th Berkeley Symp. Оn Math. Statistics and Probability. University of California Press. — 1967. — pp. 281–297.

7.      Kaufman L., Rousseeuw P. J. Clustering by means of Medoids // In Statistical Data Analysis Based on the l–Norm and Related Methods, ed. by Y. Dodge. — 1987. — pp. 405–416.

8.      Пупышева Т. Л. Морфометрия клеток фолликулярных пролифератов щитовидной железы в тонкоигольных аспиратах // Новости клинической цитологии России. — 2002. — Т.6. — № 1–2. — С.24–26.

---