Основы профессионального развития личности специалиста закладываются в вузе, начиная с первых лет обучения, в процессе усвоения специальных, общепрофессиональных, образовательных и естественно — научных предметов. Математика и физика относятся к циклу естественно — научных дисциплин и составляют фундамент инженерного образования. Они предоставляет широкие возможности для формирования профессиональных качеств личности инженера — строителя. С точки зрения развития профессиональной направленности у будущих специалистов, требования к математической подготовке инженера-строителя предполагают не только вооружение студентов определенным набором математических знаний и методов, но и предусматривают рассмотрение их практических приложений.
Целью нашего исследования является выявление уровня развития профессиональной направленности у студентов строительных специальностей первого и второго курсов вуза при изучении естественно научных дисциплин, а именно математики и физики. Нашей задачей было сравнить результаты, полученные студентами при выполнении тестовой работы и результаты, полученные на занятиях по математики и физике, где преподаватели используют задачи прикладного характера.
Учащимся предлагается тест, содержащий задачи профессионального направления, для выполнения которого необходимы знания физики и математики. Проверка смогут ли студенты применить свои знания в нестандартных, для данных предметов, задачах и является для них ведущим фактором. Результаты тестирования, в баллах, представлены в Таблице 1.
Таблица 1
|
№ учащегося |
Баллы |
|
1 |
45 |
|
2 |
38 |
|
3 |
50 |
|
4 |
29 |
|
5 |
43 |
|
6 |
55 |
|
7 |
36 |
|
8 |
48 |
|
9 |
60 |
|
10 |
58 |
|
11 |
33 |
|
12 |
40 |
Также преподавателями были проведены контрольные работы по дисциплинам математика и физика, содержащие стандартные задачи с использованием тех тем, что фигурировали в тесте. Результаты их выполнения также выставлены в баллах. Данные представлены в Таблице 2.
Таблица 2
|
№ учащегося |
Баллы по математике |
Баллы по физике |
|
1 |
42 |
44 |
|
2 |
51 |
37 |
|
3 |
46 |
58 |
|
4 |
35 |
45 |
|
5 |
58 |
56 |
|
6 |
49 |
53 |
|
7 |
38 |
50 |
|
8 |
59 |
57 |
|
9 |
54 |
48 |
|
10 |
47 |
51 |
|
11 |
40 |
46 |
|
12 |
56 |
39 |
Далее мы установим, насколько близки полученные оценки студентов при выполнении профессиональных задач, с оценками при выполнении стандартных задач дисциплин естественнонаучного цикла. С помощью ранговой корреляции коэффициента Спирмена мы сравним, насколько студенты справились с поставленными задачами. Является ли их изучение естественно научных дисциплин нацеленным на развитие профессиональной подготовки.
Составим таблицу экспериментальных данных, необходимых для расчета коэффициента корреляции Спирмена. Таблицу с рангами.
Таблица 3
|
№ учащегося |
Ранги тестирования (х1) |
Ранги экспериментальных оценок преподавателя по математики (х2) |
Ранги экспериментальных оценок преподавателя по физике (х3) |
D1 (х1-х2) |
D2 (х1-х3) |
D12 |
D22 |
|
1 |
6 |
9 |
10 |
-3 |
-4 |
9 |
16 |
|
2 |
9 |
5 |
12 |
4 |
-3 |
16 |
9 |
|
3 |
4 |
8 |
1 |
-4 |
3 |
16 |
9 |
|
4 |
12 |
11 |
9 |
1 |
3 |
1 |
9 |
|
5 |
7 |
2 |
3 |
5 |
4 |
25 |
16 |
|
6 |
3 |
6 |
4 |
-3 |
-1 |
9 |
1 |
|
7 |
10 |
12 |
6 |
-2 |
4 |
4 |
16 |
|
8 |
5 |
1 |
2 |
4 |
3 |
16 |
9 |
|
9 |
1 |
4 |
7 |
-3 |
-6 |
9 |
36 |
|
10 |
2 |
7 |
5 |
-5 |
-3 |
25 |
9 |
|
11 |
11 |
10 |
8 |
1 |
3 |
1 |
9 |
|
12 |
8 |
3 |
11 |
5 |
3 |
25 |
9 |
Нас интересует, насколько тесно связаны результаты тестирования с экспериментальными оценками по математике и физике. Проведем расчет Pэксп для двух дисциплин.
Рэмп 1 =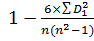 =0,45
=0,45
Pэмп 2= 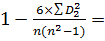 0,48
0,48
Находим по таблице критическое значение Ркр при n=12
Pкр (12; 0,05)=0,58
Получаем, что наши Рэмп 1 и Рэмп 2 не превышают Ркр. Полученный результат говорит о том, что оценки тестирования и экспериментальные оценки преподавателей отличаются незначительно. Следовательно, чем выше оценки у студентов по изучаемым дисциплинам, чем больше у них знаний по необходимым темам, тем выше их подготовка для решения профессиональных задач.
Литература:
1. Гребенев И. В., Ермолаева Е. И., Круглова С. С. Математическая подготовка абитуриентов — основа получения профессионального образования в университете // Наука и школа. 2012. № 6. С. 27–30.
2. Ермолаева Е. И. Проблемы усвоения математических знаний студентами технических вузов// Актуальные проблемы гуманитарных и естественных наук. 2010. № 7. С. 270–272.
3. Ермолаева Е. И., Куимова Е. И. О важности фундаментальной математической подготовки студентов по направлению строительство// Известия Пензенского государственного педагогического университета им. В. Г. Белинского. 2011. № 26. С. 463–467.
4. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах// Молодой ученый. 2013. № 12 (59). С. 3–6.
5. Титова Е. И., Чапрасова А. В. Коэффициент Спирмена для установления связи школьной и вузовской успеваемости по математике// Вестник магистратуры № 10(37), 2014г.







