В статье описываются особенности создания программ многомерных интервально-логических регуляторов на языках стандарта IEC 61131–3 второй редакции.
Ключевые слова: многомерная система управления, интервально-логический регулятор, языки программирования стандарта IEC 61131–3.
Многомерные интервально-логические регуляторы [1, с. 30] с переменными в виде совокупности аргументов двузначной логики (МИЛР) являются ступенью развития нечётких регуляторов в плане увеличения быстродействия автоматических систем управления и компенсации взаимного влияния контуров регулирования [2, с. 77].
В настоящее время практическое применение МИЛР сдерживается в связи с отсутствием надежных и эффективных алгоритмов их работы и, как следствие, испытаний в разных областях науки и техники.
Рассмотрим особенности программной реализации отдельных элементов (интервализаторов и деинтервализаторов) МИЛР на языках программирования контроллеров, описанных в международном стандарте IEC 61131–3.
На рис. 1, а и 1, б изображена числовая ось непрерывных физических величин #IN, #OUT с расположенными на ней термами #OUT_1 — #OUT_N, #IN_1 — #IN_N интервализатора и деинтервализатора МИЛР соответственно.
Для реализации алгоритмов интервализации МИЛР на языках стандарта IEC 61131–3 следует использовать программные элементы сравнения для установки принадлежности какой-либо входной переменной МИЛР тому или иному интервалу значений. При этом не обязательно устанавливать степень принадлежности, т. к. это значение постоянно и равно единице.
Для реализации алгоритма деинтервализации на языках стандарта IEC 61131–3 требуется выполнить проверку условия: IF #IN_N = TRUE, при выполнении которого выходной переменной #OUT будет присвоено соответствующее значение из числового интервала терма МИЛР, значение которого равно логической единице. Чёткое значение переменной #OUT определяется как функция f (#IN_N-1, #IN_N). В данном случае также необязательно указывать степень принадлежности переменной, т. к. это значение равно 1.
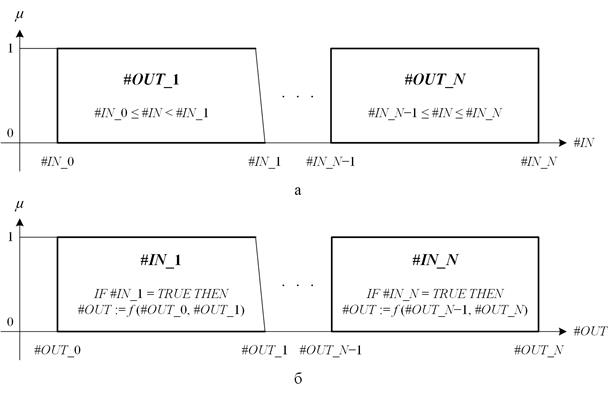
Рис. 1. Способ интерпретации непрерывных величин в виде совокупности термов: интервализатора (а) и деинтервализатора (б) МИЛР
Язык FBD (от англ. Function Block Diagram — диаграмма функциональных блоков) — представляет собой графический язык для программирования схем, состоящих из совокупности функциональных блоков, связанных между собой через входы и выходы.
Пример реализации алгоритма интервализации непрерывной физической величины IN в диапазоне значений IN_0 — IN_N на языке FBD в среде TRACE MODE 6 изображен на рис. 2, откуда видно, что FBD-программа, по сути, представляет собой цепочку последовательно выполняемых функциональных блоков, предназначенных для отработки определенных функций ("<" — сравнение, «Х||Y» — логическое ИЛИ, "!Х» — логическое НЕ, «MOVE» — пересылка значения).
Из рис. 2 следует, что с увеличением числа термов непрерывной физической величины IN в интервализаторе происходит пропорциональное увеличение числа стандартных функциональных блоков (сравнения, инверсии и др.).
Такая структура программы МИЛР в некоторой степени затрудняет дальнейшее редактирование интервализаторов в плане повышения суммарного числа термов непрерывных физических величин МИЛР и повышает её громоздкость.
Язык LAD (от англ. LAdder Diagram — многоступенчатая диаграмма) — представляет собой графический язык для программирования релейно-контактных схем, где логические выражения описываются в виде реле, и, в плане реализации алгоритмов интервализации и деинтервализации МИЛР, практически идентичен языку FBD.
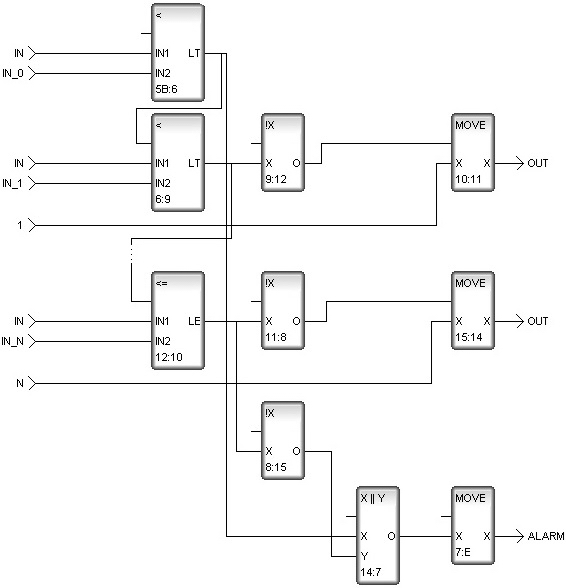
Рис. 2. Пример интервализации МИЛР на языке FBD в среде TRACE MODE
На рис. 3 изображен пример реализации алгоритма деинтервализации непрерывной физической величины OUT в числовом диапазоне значений OUT_0 — OUT_N на языке LAD в среде SIMATIC STEP 7 в процессе имитации и мониторинга переменных МИЛР.
В качестве функции деинтервализации выбрана функция для определения среднего арифметического двух аргументов (блок DIV_R). В блоке ADD_R выполнятся суммирование крайних значений интервалов термов, которые необходимо задавать непосредственно в структуре деинтервализатора.
Язык IL (от англ. Instruction List — список инструкций) — представляет собой текстовый язык для программирования мнемонических инструкций, внешне похожий на Assembler, который предоставляет гораздо больший набор инструкций, чем любой графический язык программирования, определённый стандартом IEC 61131–3.
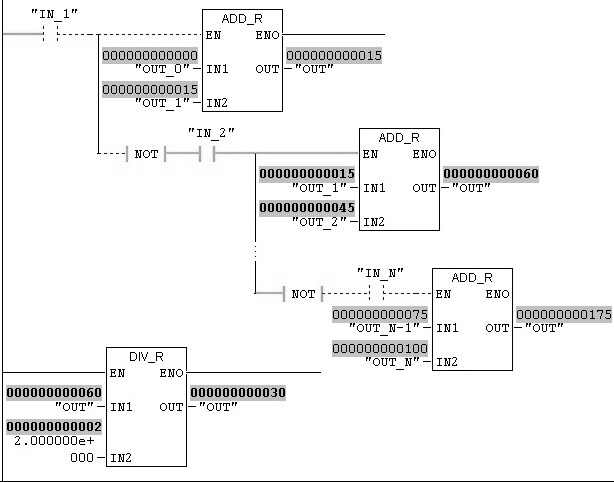
Рис. 3. Пример деинтервализации МИЛР на языке LAD в среде SIMATIC STEP 7

Рис. 4. Пример реализации STEP-TIME алгоритма интервализации МИЛР на языке программирования STL в среде разработки SIMATIC STEP 7
На рис. 4 изображен пример реализации STEP-TIME алгоритма интервализации непрерывной физической величины IN в числовом диапазоне значений IN_0 — IN_N на языке IL в среде разработки SIMATIC STEP 7. Необходимо отметить, что модификация языка IL в инструментальной среде SIMATIC STEP 7 имеет наименование STL (от англ. STatement List — лист операторов), а в среде TRACE MODE — Техно IL.
Текстовый язык высокого уровня ST (от англ. Structured Text — структурированный текст): Техно ST — в среде TRACE MODE и SCL — в среде SIMATIC STEP 7, объединяет в себе синтаксис языка Pascal и элементы, типичные для контроллеров, такие, как «вход (input)" и «выход (output)".
На рис. 5 представлен пример реализации блока логического вывода (БЛВ) на языке SCL в среде разработки SIMATIC STEP 7.

Рис. 5. Пример реализации БЛВ МИЛР на языке SCL в среде SIMATIC STEP 7
Программы, написанные на текстовых языках (IL и ST) в ряде случаев практически невозможно транслировать на графические языки (FBD и LAD), определённые стандартом IEC 61131–3, но программы, написанные на графических языках, свободно транслируются на текстовые языки. Таким образом, для полноценной реализации МИЛР-программ наиболее оптимальным вариантом будет выбор текстовых языков стандарта IEC 61131–3.
Литература:
1. Антипин А. Ф. Об одном способе анализа структуры многомерного четкого логического регулятора // Прикладная информатика. 2012. № 5. С. 30–36.
2. Антипин А. Ф. Сравнительный анализ быстродействия дискретно-логического регулятора // Программные продукты и системы. 2010. № 1. С. 75–77.







