Работа посвящена моделированию взрывного разложения микрокристаллов азида серебра, инициированного импульсом неодимового лазера наносекундной длительности. Показано, что при размерах кристаллов меньше 10 мкм критическая плотность энергии инициирования взрывного разложения значительно возрастает, что позволяет использовать такие образцы в капсюлях оптических детонаторов.
Ключевые слова: цепная модель реакции, взрывное разложение, оптический детонатор, азид серебра.
This work is devoted to the simulation of the azide silver microcrystals’ explosion decomposition, initiated by the nanosecond duration pulse of the Nd:Yag laser. It was shown that for crystals, which sizes do not exceed 10μm, the critical initiation energy density considerably increases. This fact allows to use such a samples as a cap of the optical detonators.
Keywords: chain reaction, explosive decomposition, optical detonator, silver azide.
Экспериментальные исследования кинетики процессов, приводящих к взрывному разложению энергетических материалов (ЭМ), интенсивно проводились последние пятьдесят лет. Исследования процессов взрывного разложения начинались с изучения наиболее простой системы — образцов азида серебра (АС). Азид серебра является наиболее изученным среди ЭМ, несмотря на это, причины высокой чувствительности АС к действию физических полей различной природы остаются дискуссионными [1, c. 95, 2, c. 23, 3, c. 38]. Различные группы авторов интерпретируют экспериментальные закономерности взрывного разложения с позиций микроочаговой модели теплового взрыва [4, c. 195, 5, c. 39, 6, c. 68] и вариантов моделей цепного взрыва [7, c. 14, 8, c. 97]. С позиций моделей цепного взрыва был объяснен ряд закономерностей взрывного разложения кристаллов азида серебра (АС) импульсом неодимового лазера [9, c. 15, 10, c. 5]. Вместе с тем остаются дискуссионными как сам механизм разложения, так и природа отдельных стадий. Актуальность исследования определяется необходимостью разработки оптических детонаторов на основе инициирующих и вторичных взрывчатых веществ [11, c. 5, 12, c. 79, 13, c. 341]. Первыми созданы оптические детонаторы на основе азидов серебра и свинца. Недостатком использования таких оптических детонаторов является их высокая чувствительность к лазерному импульсу, удару, трению и нагреву. Целью работы является моделирование взрывного разложения микрокристаллов АС, определение размерных характеристик азида серебра, перспективных для применения в оптическом детонаторе.
Математическая модель
В работе [9, с. 14] предложена модель твердофазной цепной реакции, способной привести к взрывному разложению азида серебра:
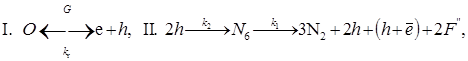 (1)
(1)
где 2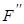 — комплекс, состоящий из двух анионных вакансий, с локализованными на них электронами. Первая стадия - генерация электронно-дырочных (e.h.) пар внешним излучением G (зарождение цепи). Обратная стадия - рекомбинация e. h. пар на объемных и поверхностных локальных центрах (обрыв цепи). Скорость рекомбинации носителей лимитируется захватом дырки на нейтральном центре: Vr ≈ kr·p [14, с. 45, 15, с. 43]. Стадия развития цепи (вторая реакция) - взаимодействие двух радикалов N30, локализованных в соседних узлах кристаллической решетки, с образованием комплекса N6. Константа скорости реакции образования N6 оценена как константа рекомбинации на отталкивающем центре [16, с. 12], k2 ≈ 10–11 ÷ 10–12 см3с-1. Далее комплекс N6 распадается на молекулярный азот (N2) и 2F-центра с выделением энергии, идущей на генерацию активных частиц — стадия разветвления цепи. Константа скорости этой реакции k1 ≈ 107 ÷ 108 с-1 оценена в работе [17, c. 19, 18, с. 607].
— комплекс, состоящий из двух анионных вакансий, с локализованными на них электронами. Первая стадия - генерация электронно-дырочных (e.h.) пар внешним излучением G (зарождение цепи). Обратная стадия - рекомбинация e. h. пар на объемных и поверхностных локальных центрах (обрыв цепи). Скорость рекомбинации носителей лимитируется захватом дырки на нейтральном центре: Vr ≈ kr·p [14, с. 45, 15, с. 43]. Стадия развития цепи (вторая реакция) - взаимодействие двух радикалов N30, локализованных в соседних узлах кристаллической решетки, с образованием комплекса N6. Константа скорости реакции образования N6 оценена как константа рекомбинации на отталкивающем центре [16, с. 12], k2 ≈ 10–11 ÷ 10–12 см3с-1. Далее комплекс N6 распадается на молекулярный азот (N2) и 2F-центра с выделением энергии, идущей на генерацию активных частиц — стадия разветвления цепи. Константа скорости этой реакции k1 ≈ 107 ÷ 108 с-1 оценена в работе [17, c. 19, 18, с. 607].
Из всех реагентов, рассматриваемых в модели (1), передвигаться по кристаллу (и диффундировать) за время развития взрывного разложения способны только электронные носители заряда. Коэффициент диффузии для дырок и электронов, составляет Dp ≈ Dп ≈ 0.25 см2/с [10, c. 6].
Рассмотрим инициирование прямоугольного монокристалла размерами a´b´c. Точку отсчета декартовой системы координат поместим в одной из вершин кристалла так, чтобы ребра образца совпадали с осями координат x, y, z и отсекали на них отрезки a, b, c соответственно. Импульс излучения падает перпендикулярно передней грани образца (x = 0), и имеет сечение значительно большее, чем данная грань кристалла (Su >> bc), что обеспечивает равномерную освещенность поверхности образца. Рассмотрим влияние поверхности образца на кинетику развития цепной реакции инициирования АС импульсным излучением. С учетом влияния поверхности система дифференциальных уравнений, описывающих кинетику процесса, будет иметь вид:
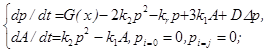 (2)
(2)
где, 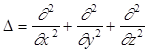 — оператор Лапласа в прямоугольной системе координат, i = x, y, z для j = a, b, c — соответственно, A — концентрация комплексов N6.
— оператор Лапласа в прямоугольной системе координат, i = x, y, z для j = a, b, c — соответственно, A — концентрация комплексов N6.
Результаты расчетов
Как показали результаты расчета, после действия импульса в образце устанавливается распределение реагентов по кристаллу, соответствующее стоячей волне, что позволяет упростить (2):
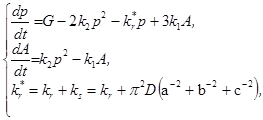 (3)
(3)
где 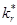 — эффективная константа «рекомбинации» с учетом влияния поверхности. Величина константы скорости поверхностной рекомбинации (ks) зависит только от размеров образца и коэффициента диффузии носителей, физически это означает, что при большой скорости поверхностной рекомбинации лимитирующей стадией процесса является приток частиц к поверхности образца [10, c. 7]. Подробный анализ решения системы (3) с
— эффективная константа «рекомбинации» с учетом влияния поверхности. Величина константы скорости поверхностной рекомбинации (ks) зависит только от размеров образца и коэффициента диффузии носителей, физически это означает, что при большой скорости поверхностной рекомбинации лимитирующей стадией процесса является приток частиц к поверхности образца [10, c. 7]. Подробный анализ решения системы (3) с 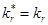 проведен в работах [19, c. 158]. Зависимость критической плотности энергии инициирования от размеров образца при малых длительностях импульса имеет вид:
проведен в работах [19, c. 158]. Зависимость критической плотности энергии инициирования от размеров образца при малых длительностях импульса имеет вид:
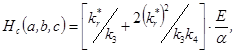 (4)
(4)
где Е — ширина запрещенной зоны и a — коэффициент поглощения являются фундаментальными характеристиками и слабо изменяются от кристалла к кристаллу. Из (4) следует, что с уменьшением величины минимального размера кристалла определяющего поверхностную рекомбинацию на максимальных по площади гранях критическая плотность энергии возрастают.
При больших длительностях импульса критическим параметром перехода реакции разложения АС в самоускоряющийся режим становится плотность мощности импульса. Зависимость критической плотности мощности инициирования от размеров образца определяется выражением [19, c. 158]:
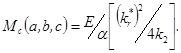 (5)
(5)
Обозначив за z коэффициент, учитывающий вклад остальных граней образца, получаем следующее выражение для определения эффективной константы рекомбинации 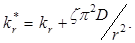
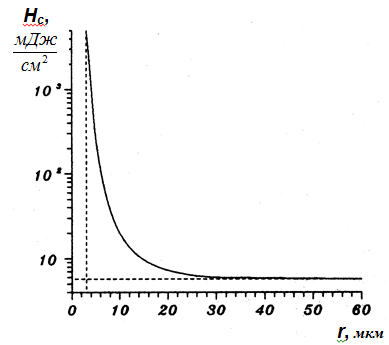
Рис. 1. Рассчитанная по системе (2) зависимость критической плотности энергии инициирования АС импульсным излучением от характерного размера образца
Максимальное значение z возможно у кубического кристалла (a = b = c), а в случае уже четырехкратного превышения длин максимальных ребер образца над минимальными (4a £ b, 4a £ c), значение z можно принять за единицу. Физически это означает, что поверхностное время жизни реагентов определяется рекомбинацией на максимальных по площади гранях и можно пренебречь диффузией носителей к другим граням. В проведенном рассмотрении предполагалось, что скорость рекомбинации носителей на различных кристаллографических гранях одинакова, в противном случае существенен учет диффузии носителей только к рекомбинационно-активным граням, что дополнительно понижает размерность задачи. Размерные эффекты будут существенно сказываться при 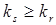 , что соответствует размерам кристалла 10 мкм.
, что соответствует размерам кристалла 10 мкм.
На рисунке 1 показана рассчитанная по системе (2) зависимость критической плотности энергии инициирования от характерного размера образца. При r< 10 мкм значение критической плотности энергии резко повышается и при r = 1 мкм Hc @5Дж/cм2. При таких больших плотностях возбуждения меняется характер кинетики начальных стадий процесса: разложение образца (по анионной подрешетке) достигает значительной величины уже на стадии индукционного периода, следовательно, необходим учет выгорания, что будет сделано в дальнейшем.
Таким образом, интервал размеров кристалла, в котором критическая плотность энергии инициирования зависит от r, не зависит от параметров инициирующего импульса, а определяются физико-химическими характеристиками кристаллов: коэффициентом диффузии электронных носителей заряда, константами скоростей элементарных стадий развития и обрыва цепи. Проведенное исследование открывает возможность направленно регулировать чувствительность АС за счет изменения размеров микрокристаллов. Повышенные значения пороговой плотности энергии инициирования взрывного разложения кристаллов АС менее 10 мкм позволяют использовать их в качестве капсюлей оптического детонатора.
Литература:
1. Адуев, Б. П. Дивакансионная модель инициирования азидов тяжелых металлов/ Б. П. Адуев, Э. Д. Алукер, А. Г. Кречетов// Физика горения и взрыва. — 2004. — Т. 40. — № 2. — С. 94–99.
2. Кригер, В. Г. Определение пространственных характеристик волны цепной реакции в азиде серебра./ В. Г. Кригер, А. В. Каленский, А. А. Звеков, М. В. Ананьева, А. П. Боровикова, И. Ю. Зыков// Химическая физика. — 2014. — Т. 33. — № 8. — С. 22–29.
3. Боровикова, А. П. Пространственно-временные характеристики волны горения в азиде серебра/ А. П. Боровикова, А. В. Каленский, И. Ю. Зыков// Аспирант. — 2014. — № 3. — С. 37–42.
4. Ананьева, М. В. Кинетические закономерности взрывного разложения ТЭНа, содержащего наноразмерные включения алюминия, кобальта и никеля / М. В. Ананьева, А. В. Каленский, Е. А. Гришаева, И. Ю. Зыков, А. П. Никитин// Вестник КемГУ. — 2014. — № 1–1(57). — С. 194–200.
5. Адуев, Б. П. Взрывчатое разложение ТЭНа с нанодобавками алюминия при воздействии импульсного лазерного излучения различной длины волны / Б. П. Адуев, Д. Р. Нурмухаметов, Р. И. Фурега, А. А. Звеков, А. В. Каленский// Химическая физика. — 2013. — Т.32. — № 8. — С. 39–42.
6. Никитин, А. П. Расчет критических параметров инициирования теплового взрыва тэна с наночастицами меди на разных длинах волн/ А. П. Никитин// Международное научное издание Современные фундаментальные и прикладные исследования.– 2013. — № 4(11).– С. 68–75.
7. Anan’eva, M.V. Comparative analysis of energetic materials explosion chain and thermal mechanisms / M. V. Anan’eva, V. G. Kriger, A. V. Kalenskii, A. A. Zvekov, A. P. Borovikova, E. A. Grishaeva, I.Yu. Zycov // Известия высших учебных заведений. Физика. — 2012. — Т.55. — № 11–3. — С. 13–17.
8. Боровикова, А. П. Методика моделирования распространения взрывного разложения азида серебра / А. П. Боровикова, А. В. Каленский// Аспирант. — 2014. — № 4. — С. 96–100.
9. Кригер, В. Г. Механизм твердофазной цепной реакции/ В. Г. Кригер, А. В. Каленский, Ю. А. Захаров, В. П. Ципилев// Материаловедение. — 2006. — № 9. — С. 14–21.
10. Кригер, В. Г. Пороговая энергия инициирования азида серебра эксимерным лазером/ В. Г. Кригер, А. В. Каленский, В. В. Коньков// Материаловедение. — 2003. — № 7. — С. 2–8.
11. Ананьева, М. В. Перспективные составы для капсюля оптического детонатора/ М. В. Ананьева, А. А. Звеков, И. Ю. Зыков, А. В. Каленский, А. П. Никитин// Перспективные материалы. — 2014. — № 7. — С. 5–12.
12. Зыков, И. Ю. Критическая плотность энергии инициирования тэна с добавками наночастиц алюминия/ И. Ю. Зыков// Международное научное издание Современные фундаментальные и прикладные исследования. — 2013. — № 1(8).– С. 79–84.
13. Каленский, А. В. Спектральная зависимость критической плотности энергии инициирования композитов на основе пентаэритриттетранитрата с наночастицами никеля/ А. В. Каленский, М. В. Ананьева, А. А. Звеков, И. Ю. Зыков// Фундаментальные проблемы современного материаловедения. — 2014. — Т.11. — № 3. — С. 340–345.
14. Гришаева, Е. А. Неизотермическая модель разветвленной цепной реакции взрывного разложения энергетических материалов / Е. А. Гришаева, А. В. Каленский, М. В. Ананьева, А. А. Звеков// Фундаментальные проблемы современного материаловедения. — 2013. — Т.10. — № 1. — С. 44–49.
15. Боровикова, А. П. Природа стадии обрыва цепи разветвленных твердофазных цепных реакций/ А. П. Боровикова, М. В. Ананьева, О. В. Одинцова// Молодой ученый. — 2014. — № 15(74). — С. 41–45.
16. Каленский, А. В. Коэффициент захвата электронных носителей заряда на экранированном отталкивающем центре/ А. В. Каленский, М. В. Ананьева, В. Г. Кригер, А. А. Звеков// Химическая физика. — 2014. — Т. 33. — № 4. — С. 11–16.
17. Кригер, В. Г. Релаксация электронно-возбужденных продуктов твердофазной реакции в кристаллической решетке / В. Г. Кригер, А. В. Каленский, А. А. Звеков // Химическая физика. — 2012. — Т.31. — № 1. — С. 18 - 22.
18. Каленский, А. В. Моделирование граничных условий при квантово-химических расчетах азидов металлов в кластерном приближении / А. В. Каленский, Л. Г. Булушева, В. Г. Кригер, Л. Н. Мазалов// Журнал структурной химии. — 2000. — Т. 41. — № 3. — С. 605–608.
19. Кригер, В. Г. Инициирование азидов тяжелых металлов импульсным излучением / В. Г. Кригер, А. В. Каленский // Химическая физика. — 1995. — Т. 14. — № 4. — С. 152–160.
[1] Работа выполнена при финансовой поддержке РФФИ (грант № 14–03–00534 А) и Министерства образования и науки РФ (госзадание № 2014/64).







