В статье описывается способ построения многомерных систем управления на основе интервально-логических регуляторов с компенсацией взаимного влияния контуров регулирования.
Ключевые слова: многомерная система управления, интервально-логический регулятор, компенсация взаимного влияния контуров регулирования.
Известно [1, с. 100], что к многомерным системам управления относятся системы, у которых имеется несколько взаимосвязанных управляемых и управляющих физических величин, например, системы автоматического регулирования (САР) напряжения или частоты синхронного генератора, САР частоты вращения двигателей переменного тока и т. д.
Многомерная система управления (СУ) предполагает наличие многомерного объекта управления (МОУ), который характеризуется входными управляющими переменными и возмущающими воздействиями, выходными (регулируемыми) и промежуточными (внутренними) переменными, что являются, по существу, векторными величинами, зависящими от времени.
На рис. 1 приведена сокращённая структурная схема многомерной СУ, где векторы u, f и y образуют соответствующие пространства управляющих, возмущающих и регулируемых величин; вектор заданий g в каждый момент времени t образует пространство заданных величин; МР — многомерный регулятор [2, c. 75].
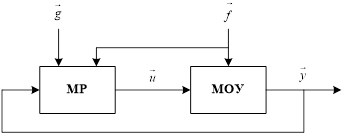
Рис. 1. Схема многомерной системы управления
Основной проблемой систем, относящихся к классу многомерных, является значительное взаимное влияние их параметров при поддержании значений регулируемых величин в требуемом числовом диапазоне. Кроме того, многомерные системы характеризуются рядом особенностей, к которым можно отнести высокую сложность при большом числе каналов, высокий порядок соответствующих дифференциальных уравнений, трудности при определении структуры регуляторов и обеспечении требуемых динамических свойств и т. д. Очевидно, что при разработке многомерных регуляторов основной проблемой является развязка каналов. В связи с этим при их синтезе необходимо учитывать перекрёстные связи. Задачей синтеза многомерной системы управления, в первую очередь, является исключение взаимного влияния каналов за счет введения дополнительных связей, то есть важно настроить каждый контур регулирования с учётом влияния смежных контуров.
В многомерном нечётком интервально-логическим регуляторе (МИЛР), разработанном автором, каждому терму T непрерывной физической величины x на заданном отрезке универсальной числовой оси отводится отдельный участок, который не перекрывается соседними термами. Данное обстоятельство позволяет каждое чёткое значение непрерывной физической величины представить одним и только одним термом, что наиболее адекватно идентифицирует эту величину в виде совокупности аргументов двузначной логики.
На рис. 2 представлены варианты интерпретации непрерывной физической величины x совокупностью термов T, где для каждого терма однозначно определён покрываемый им отрезок числовой оси. Так, на рис. 2, б) терм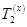 
покрывает
на оси отрезок 
.
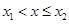При прямом характере определения принадлежности термов непрерывной величины x (рис 2, а, в) терм-множество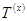 
аналитически можно представить в виде
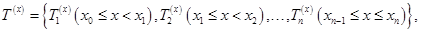
а его рекуррентную форму в виде
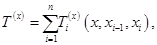
где знак суммы обозначает совокупность термов непрерывной физической величины x.
При обратном характере определения принадлежности термов непрерывной величины x (рис 2, б, г) терм-множество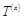 
аналитически можно представить в виде
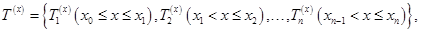
а его рекуррентная форма останется неизменной.
Значения x0 и xn определяют диапазон распределения термов T непрерывной величины x на числовой оси.
Так как термы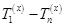 
представляют собой однозначно определённые множества, их функции принадлежности 
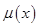будут иметь прямоугольную форму. Значение функций принадлежности будет равно единице для всех термов T непрерывной величины x. Это обстоятельство указывает на то, что термы T являются по своей природе булевыми переменными, которые принимают значение равное логической единице на тех участках числовой оси непрерывной физической величины x, где функция принадлежности термов равна 1, и, наоборот, логическому нулю, где функция принадлежности термов равна 0.
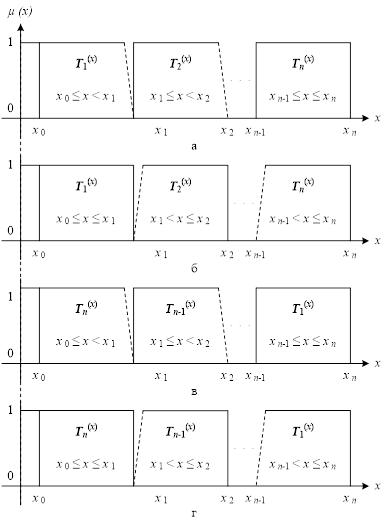
Рис. 2. Способ интерпретации непрерывной физической величины x в виде совокупности термов T с прямым (а, б) и обратным (в, г) порядком распределения термов, и с прямым (а, в) и обратным (б, г) характером определения принадлежности термов
Концепция построения СУ на основе МИЛР состоит из следующих положений:
1) текущее и заданное значения непрерывных величин сравниваются единожды — в условной части системы интервализаторов (фаззификаторов) в процессе их интерпретации эквивалентными совокупностями термов;
2) для повышения быстродействия процедуры интервализации (фаззификации) непрерывных величин её необходимо прервать после определения терма, значение которого равно логической единице;
3) в любой момент t существует один и только один терм в совокупности термов T, определяющих непрерывную величину, значение которого равно логической единице. Значения остальных термов T в указанной совокупности в момент t равны логическому нулю. Это положение следует из факта, что любая непрерывная величина в каждый момент времени t может иметь одно и только одно чёткое значение;
4) в любой момент t система продукционных правил, относящаяся к конкретной регулируемой непрерывной величине, содержит одно и только одно правило, антецедент которого равен логической единице. В связи с этим, в каждом цикле сканирования достаточно определить только «истинное» правило, а не обрабатывать систему правил целиком, что может быть достигнуто в результате введения соответствующего механизма [3, с. 33].
Отличительной особенностью МИЛР от других нечетких регуляторов является деление системы продукционных правил (СПП) на регулирующую и компенсационную составляющие (РСПП и КСПП соответственно).
Компенсационная СПП позволяет решить главную проблему синтеза многомерных регуляторов, и служит для исключения в установившемся режиме взаимного влияния контуров регулирования друг на друга.
На рис. 3 представлена упрощённая схема СУ на базе МИЛР с компенсацией влияния на отдельно взятый контур всех остальных контуров регулирования, где З(t), Z(t), U(t) — векторы задающих, регулируемых и регулирующих параметров соответственно, а TЗZ и UT — векторы их термов; XБ и YБ — дискретные входные и выходные сигналы МОУ соответственно; БЛВ — блок логического вывода.
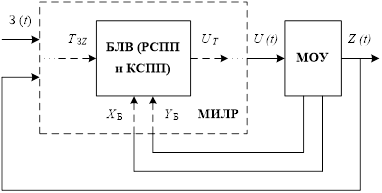
Рис. 3. Схема СУ на базе МИЛР с компенсацией взаимного влияния контуров
Источником информации при разработке СПП МИЛР являются экспериментально снятые зависимости задающего и регулируемого параметров в автономном и многосвязном режимах работы. В связи с тем, что в условной части продукционных правил имеется возможность использовать термы, как входных, так и выходных параметров, информацию для разработки КСПП предлагается получать из двух и более экспериментов при работе МИЛР с реальным МОУ. В ходе первого эксперимента снимаются зависимости управляющих воздействий от задающих параметров в автономном режиме работы контуров регулирования МИЛР, что достигается в результате отключения всех контуров, кроме того, на котором в данный момент времени t снимается указанная зависимость. В ходе второго и, при необходимости, последующих экспериментов для каждого контура регулирования при одинаковых значениях задающего параметра снимаются те же зависимости, но при работе остальных контуров регулирования МИЛР в штатном режиме.
На рис. 4 приведены графики зависимости управляющего воздействия Ui от задающего параметра Зi i-го канала МИЛР: Uai — в автономном (сепаратном) режиме, Umi — в режиме взаимного влияния контуров. Кривая Umi приведена для i-го контура регулирования МИЛР. Аналогичные зависимости требуется получить для остальных контуров регулирования МИЛР. На рис. 4 заштрихованная площадь характеризует степень влияния на i-ый контур остальных (n-i) контуров регулирования МИЛР. Эта характеристика в более лаконичной и удобной форме представлена на рис. 5 в виде разностной функции
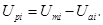
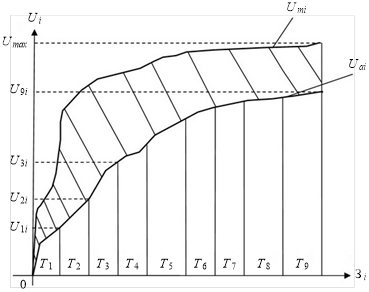
Рис. 4. Графики зависимости Ui от задающего параметра Зi i-го канала МИЛР
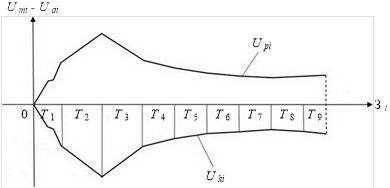
Рис. 5. Графики разностной функции Uрi и функции компенсации Uki влияния (n-i) контуров на i-й контур регулирования МИЛР
Смысл компенсации взаимного влияния контуров регулирования МИЛР заключается в выработке при помощи специальной системы правил функции, характеризующей степень влияния на i-ый контур остальных контуров регулирования МИЛР. Функция Uki является зеркальным отображением экспериментально полученной функции Uрi относительно оси абсцисс Зi. При точном отображении функция Uki скомпенсирует влияние (n-i) контуров на i-ый контур регулирования МИЛР [4, с. 32].
Для интерпретации Uki в виде совокупности аргументов двузначной логики используются термы Т1, …, Т9, которые вырабатываются из условий:
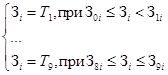или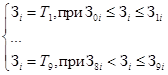 
в зависимости от характера (прямой или обратный) определения принадлежности термов.
СПП, реализующая компенсирующую функцию Uki для i-го контура регулирования МИЛР с помощью термов Т1, …, Т9, имеет следующий вид:
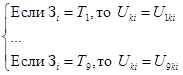
В общем случае количество термов T для представления функции Uki определяется точностью регулирования и разрешающей способностью программируемого контроллера, ресурсы которого задействованы при разработке МИЛР.
Воспроизведение компенсирующих функций для остальных контуров регулирования производится аналогично.
Предложенный способ позволяет повысить характеристики регулирования, а также расширить область применения МИЛР.
Литература:
1. Артамонов Д. В., Семенов А. Д. Основы теории линейных систем автоматического управления: Учебное пособие. — Пенза: Изд-во Пенз. гос. ун-та, 2003. — 135 с.
2. Антипин А. Ф. Сравнительный анализ быстродействия дискретно-логического регулятора // Программные продукты и системы. 2010. № 1. С. 75–77.
3. Антипин А. Ф. Особенности программной реализации многомерных логических регуляторов с переменными в виде совокупности аргументов двузначной логики // Автоматизация и современные технологии. 2014. № 2. С. 30–36.
4. Антипин А. Ф. Об одном способе анализа структуры многомерного четкого логического регулятора // Прикладная информатика. 2012. № 5. С. 30–36.
