В статье описаны наиболее распространенные индексы пространственно-территориальных сопоставлений, изложены результаты их исследования, определено соответствие требованиям.
Ключевые слова: статистика, индексы пространственно-территориальных сопоставлений.
На практике достаточно часто возникает потребность в сравнении уровней экономических явлений, наблюдаемых на различных территориях.
Наука, в частности статистика, решает эту задачу с помощью индексов пространственно-территориальных сопоставлений [1].
Индексы пространственно-территориальных сопоставлений — это индексы, которые позволяют сравнить между собой уровни одних и тех же экономических явлений, наблюдающихся на разных территориях.
Таким образом, рассмотрение этих индексов, по нашему мнению, более чем обоснованно.
Во-первых, в последнее время в статистике относительные показатели все чаще стали называть индексы (например, темп роста — индекс роста и т. п.). В предлагаемой работе межрегиональные сопоставления предлагается делать на основании относительных показателей, а, следовательно, требования, предъявляемые к индексам территориально-пространственных сопоставлений, целесообразно использовать для относительных показателей.
Во-вторых, выполнение требований позволит оценить и сгладить отраслевые различия в структуре развития регионов, или в случае невозможности сглаживания, исключить данные регионы или показатели из анализа.
В-третьих, территориальные сопоставления нередко необходимо осуществлять одновременно для группы субъектов, поэтому необходимо согласовывать индексы, исчисленные для всей группы областей.
Основные требования к территориальным индексам, а, следовательно, и для базисных темпов роста можно сформулировать следующим образом.
1. Характерность весов, то есть для показателей двух регионов А и Б в качестве весов должны использоваться показатели этих стран А и Б (или средние из них), показатели какой-либо третьей страны.
2. Независимость от выбора базисной страны (требование обратимости индексов во времени, адаптированное к территориальным сопоставлениям):
,
где IА/Б — индекс цен (физического объема) страны А по отношению к стране Б;
IБ/А — индекс цен (физического объема) страны Б по отношению к стране А.
3. Транзитивность, то есть:
где IА/В — индекс цен (физического объема) страны А по отношению к стране В;
IБ/В — индекс цен (физического объема) страны Б по отношению к стране В.
Суть требования транзитивности состоит в том, что индекс, полученный для некоторой пары стран А и Б путем прямого сопоставления их цен (физического объема), должен быть равен этому же индексу, полученному косвенным путем, то есть делением индекса IА/В на индекс IБ/В.
4. Аддитивность. Индексы цен (физического объема), рассчитанные для всей совокупности товаров и услуг, должны быть четко согласованы с индексами, исчисленными для всех групп этой совокупности.
5. Требование факторной пробы, которое означает, что произведение индекса цен и индекса физического объема должно быть равно индексу стоимости:
.
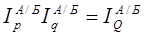В теории и практике международных сопоставлений различают прямые парные и многосторонние сопоставления. Каждые имеют свою специфику, поэтому для их проведения используют различные формулы индексов.
Прямые парные сопоставления проводятся для какой-либо изолированной пары стран (например, для России и США), на которые не влияют показатели третьих стран. Для таких сопоставлений важным является требование характерности весов, факторной пробы и независимости от выбора базисной страны. Это важно учитывать и при сопоставлении отдельных территорий (регионов), имеющих специфическую специализацию.
Многосторонние сопоставления проводятся одновременно для группы регионов.
Для межстрановых сопоставлений использует паритеты покупательной способности (ППС) валют, для сопоставления данных социально-экономического развития регионов внутри страны, т. е. в условиях действия одной валюты, достаточно использовать индекс потребительских цен или индексы цен производителей различных видов экономической деятельности (ВЭД) (промышленностью строительство и т. д.).
Учитывая, что в некоторых работах используется сопоставление ВРП для проведения многосторонних сопоставлений целесообразно использовать формулы ЭКШ, Гири-Камиса, Уолша и Джерарди, которые удовлетворяют требованию транзитивности.
Наиболее часто используется формула ЭКШ[1], которая представляет собой среднюю геометрическую из индексов Фишера для любой пары сравниваемых территорий А и Б, исчисленных косвенным путем, т. е. через третью территорию j:
, (1)
где 
– индекс Фишера для территорий А и Б; 
– индекс Фишера для территории А и j; 
– индекс Фишера для территории j и Б; n — число территорий, участвующих в сопоставлении.
Недостатком формулы (1) является то, что она не удовлетворяет требованию аддитивности. Этого недостатка нет у формулы Гири-Камиса, которая позволяет исчислять средние межтерриториальные цены на различные группы товаров, выраженные в единицах валюты страны, по отношению друг к другу:
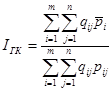, (2)
где qij– количество i-го товара в j-ом регионе;
pij– цена i-го товара в j-ом регионе;
– средняя по стране цена i-го товара.
Недостатком формулы является то, что она не удовлетворяет требованию характерности весов.
Еще один метод территориальных сопоставлений, для которого разработана особая форма индекса, носит название метода Уолша, формула которого имеет следующий вид:
, (3)
где 
– средний индекс цен для i-ой товарной группы в регионе А по сравнению с регионом Б; 
– средняя доля i-ой товарной группы для всей совокупности территорий, принимающих участие в сопоставлении.
По формуле (2) рассчитывается средний геометрический индекс, взвешенный по средним весам для группы территорий, участвующих в сопоставлении; в качестве этих средних весов выступают средние (для всей совокупности регионов) доли товарных групп в соответствующих показателях (например, в ВВП). Формула удовлетворяет требованиям транзитивности и независимости от выбора базисной страны, но не удовлетворяет требованию аддитивности, а также в меньшей мере, чем индексы ЭКШ, удовлетворяет требованию характерности весов.
В практике международных сопоставлений ВВП, проводимых в рамках ЕС, в течение нескольких лет применялся метод Джирарди, в основе которого лежит исчисление индексов физического объема выпуска и валового регионального продукта (ВРП) различных регионов с помощью оценки ВРП в средних ценах, получаемых по формуле средней геометрической простой. Этот метод похож на метод Гири-Камиса, однако, в отличие от него средние цены исчисляются здесь по формуле средней геометрической простой (а не по формуле средней арифметической взвешенной, как в методе Гири-Камиса).
При территориальном сопоставлении макроэкономических показателей и стоимостных показателей социально-экономического развития широко применяется метод цепных индексов, когда в рамках некоторой группы регионов интересующий показатель (например, ВРП) сравнивается с этим показателем какой-либо одной базисной территории, тогда анализируемые показатели каждой из этой группы регионов, кроме базисного, сравниваются с помощью цепных индексов, то есть по отношению к базисной территории.
Наиболее распространенным методом построения территориальных весов в практике, особенно для межрегиональных сравнений, является метод стандартных весов. Этот метод заключается в том, что значение индексируемой величины взвешиваются не по всем весам отдельной территории, а по суммарным весам изучаемых регионов.
Литература:
1. Коржова Г. И. Разработка теоретических предложений по совершенствованию методики оценки органов исполнительной власти регионов РФ и местного самоуправления [Текст] / Г. И. Коржова, В. В. Коварда, О. А. Сусликова // Молодой ученый. — 2014. — № 5. — С. 270–272.
[1] В названии использованы начальные буквы фамилий трех статистиков, предложивших этот индекс: венгров Элтетэ и Кэвеша и поляка Шульца
