Проведены исследования переходных процессов при распространении волн напряжений в сферическом теле в случае когда контактные усилия и закон расширения зоны контакта заменены заданной подвижной ударной нагрузкой. Разработан и реализован алгоритмучета разгрузки.
Ключевые слова: контактная задача, ударная нагрузка, упруго-пластическая сфера, волна разгрузки, переходной процесс, подвижная нагрузка.
Axisymmetric dynamic problem of loading of the elastic-plastic sphere under the action of the movable load
The study of transient processes in the propagation of waves of tension both in the spherical body when the contact forces and the law of extension of the contact zone are replaced by the given mobile shock. Developed and implemented accounting unloading.
в процессе исследования рассматривается осесимметричная нестационарная задача о нагружении сферического тела подвижной нагрузкой, распространяющейся по ее внешней поверхности со скоростью γ.
Задача о деформировании твердых тел с подвижными нагрузками тесно примыкает к задачам соударения [1], являясь их первым приближением. Это следует из того, что в некоторых случаях воздействие одного тела на другое может быть заменено заданной нагрузкой, интенсивность и закон распространения которой определяется из геометрических, физических или каких-либо иных соображений.
Материальные точки сферического тела имеющего в сечении форму кольца с внутренним 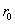 и внешним
и внешним 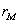 радиусами, относятся к сферической системе координат
радиусами, относятся к сферической системе координат 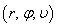 . Из за осевой симметрии движение точек тела, достаточно рассмотреть в меридиональной плоскости
. Из за осевой симметрии движение точек тела, достаточно рассмотреть в меридиональной плоскости 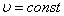 . Определим в ней расчетную область, имеющую форму прямоугольника (рис. 1).
. Определим в ней расчетную область, имеющую форму прямоугольника (рис. 1).
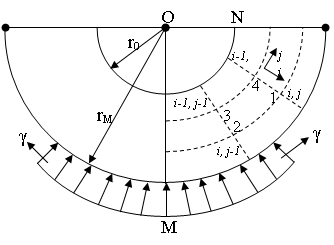
Рис. 1
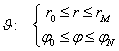
где 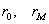 — соответственно внутренний и внешний радиусы сферической оболочки;
— соответственно внутренний и внешний радиусы сферической оболочки;
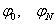 — боковые границы сферы.
— боковые границы сферы.
Алгоритм расчета пространственной задачи основан на лагранжевых конечных элементах (кэ) и обобщенный алгоритм совпадает с алгоритмом описанным в работе [1]. При этом расчетная область разбивается на элементарные ячейки прямоугольной формы регулярной сеткой координатных линий [2]:
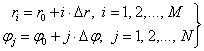 (1)
(1)
где 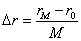 ,
, 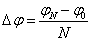 — шаги сетки разбиения.
— шаги сетки разбиения.
Объем элемента равен объему тела вращений ячейки расчетной области вокруг оси симметрии на единичный угол.
Внутри каждого элемента неизвестные функции перемещений с составляющими
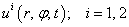
представляются в виде разложения
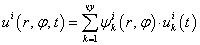 , (2)
, (2)
где 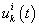 — узловые значения составляющих перемещений;
— узловые значения составляющих перемещений;
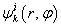 — специальным образом подобранные функции координат со следующими свойствами:
— специальным образом подобранные функции координат со следующими свойствами:
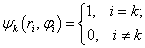
выбор которых обусловлен непрерывностью перемещений между узлами;
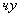 — число узлов в элементе;
— число узлов в элементе;
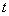 — время.
— время.
Вычисляя соответствующие производные по пространственным переменным, из (2) можно получить выражения для компонент тензора малых деформаций [3]:
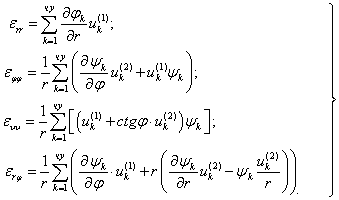 (3)
(3)
Связь напряжений и деформаций устанавливается на основании законов деформационной теории пластичности [3] в виде
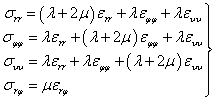 (4)
(4)
Здесь обобщенные модули являются функциями инвариантов тензора деформаций:
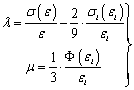 ,
,
где 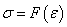 — закон сжимаемости;
— закон сжимаемости;
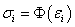 — закон эластичности;
— закон эластичности;
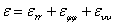 — относительная объемная деформация;
— относительная объемная деформация;
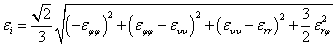 — интенсивность деформаций.
— интенсивность деформаций.
В решении задачи могут быть самопроизвольные разрывы (скачки) и сохранение внутренней энергии теряется, даже когда некоторые другие законы сохранения массы и моменты выполняются. Здесь используется такой прием как рассеивание энергии, с помощью искусственной вязкости. Последняя учитывается в уравнении движения дискретной модели как добавок к действующим напряжениям:
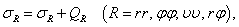
где 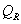 — компоненты псевдовязкостных напряжений.
— компоненты псевдовязкостных напряжений.
Уравнения движения выводятся на основе вариационного принципа Гамильтона-Остроградского и имеют следующий вид:
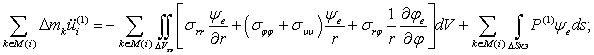
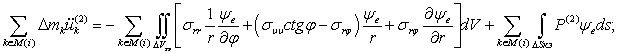
Здесь 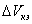 — объем элемента;
— объем элемента;
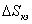 — площадь поверхности элемента;
— площадь поверхности элемента;
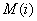 — множество кратных элементов в узле с номером i;
— множество кратных элементов в узле с номером i;
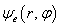 — функции формы;
— функции формы;
e — локальный номер i в элементе k;
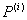 — заданные составляющие поверхностного давления;
— заданные составляющие поверхностного давления;
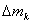 — доля общей массы элемента, сосредоточенная в его k-м узле с весом
— доля общей массы элемента, сосредоточенная в его k-м узле с весом 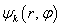 ;
;
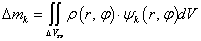 , где
, где 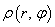 — плотность среды в элементе.
— плотность среды в элементе.
При расчетах полагаем, что границы расчетной области свободны от усилий:
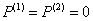 при
при 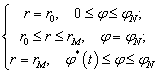 ,
,
кроме части внешней границы, на которой задано давление
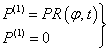 при
при 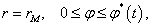 где координата крайней точки подвижной нагрузки определяется из уравнения
где координата крайней точки подвижной нагрузки определяется из уравнения
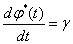
Условия симметричности удовлетворяются с помощью ряда ячеек за осью симметрии, куда засылаются параметры из смежных ячеек среды, т. е. на оси симметрии выполняются условия:
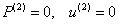 .
.
Рассматриваются варианты, когда экспериментальные связи между инвариантами, тензора напряжений и деформаций аппроксимируются линейными и квадратичными функциями.
Особое место занимает случай, когда кривая разгрузки не совпадает с кривой нагружения. В этом случае для замыкания задачи необходимо определить значения объёмной деформации 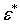 и интенсивности деформаций
и интенсивности деформаций 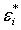 , соответствующие началу разгрузки. Для этого на каждом временном слое в каждом элементе для каждого узла интегрирования проверяется выполнение условий:
, соответствующие началу разгрузки. Для этого на каждом временном слое в каждом элементе для каждого узла интегрирования проверяется выполнение условий:
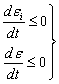 ,
,
при которых соответствующие значения объемной деформации и интенсивности деформаций принимаются за 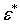 и
и 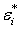 . При этом процессе разгрузки будет происходить до тех пор, пока соответствующие значения
. При этом процессе разгрузки будет происходить до тех пор, пока соответствующие значения 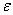 и
и 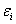 не будут превосходить
не будут превосходить 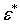
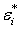 .
.
Экспериментальные кривые, характеризующие объемное сжатие и деформацию сдвига, аппроксимируются следующим образом:
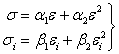 в случае нагрузки;
в случае нагрузки;
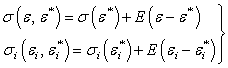 в случае разгрузки.
в случае разгрузки.
Здесь напряжения отнесены к величине 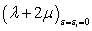 и безразмерные величины согласно экспериментам имеют значения:
и безразмерные величины согласно экспериментам имеют значения:
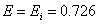 ,
, 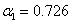 ,
, 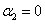 ,
, 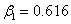 ,
, 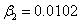 (5) (нелинейно-упругий материал).
(5) (нелинейно-упругий материал).
Расчеты проводились на сетке 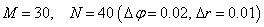 с заданной нагрузкой в виде
с заданной нагрузкой в виде 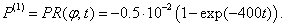
На рис. 2 и 3 показаны графики изменения компонент напряжений 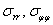 на оси симметрии в точках с координатами (1, 0), (0.95, 0), (0.9, 0)
на оси симметрии в точках с координатами (1, 0), (0.95, 0), (0.9, 0)
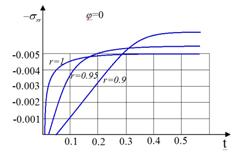
Рис. 2.
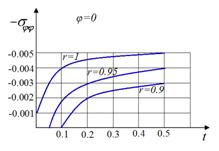
Рис. 3.
На рис. 4 приведены графики изменения координаты пересечения фронтов продольной волны (кривая 1) и волны разгрузки (кривая 2) с осью симметрии. Численные эксперименты показывает, что скорость волны разгрузки вдвое меньше скорости продольной волны в сечении 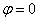 .
.
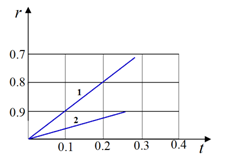
Рис. 4.
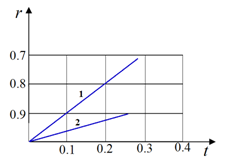
Рис. 5.
Влияния искусственной вязкости можно проследить на рис. 5.
При расчетах без искусственной вязкости (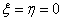 — сплошная кривая) в зонах больших градиентов скоростей деформаций и напряжений имеют место колебания указанных величин. Для сравнения на последнем рисунке приведена пунктирная кривая, полученная с использованием искусственной вязкости (
— сплошная кривая) в зонах больших градиентов скоростей деформаций и напряжений имеют место колебания указанных величин. Для сравнения на последнем рисунке приведена пунктирная кривая, полученная с использованием искусственной вязкости (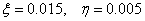 ). При этом экспериментальные кривые аппроксимируются в виде квадратичной функции с параметрами (5). Расчет проведен на сетке М=50, N=40 (
). При этом экспериментальные кривые аппроксимируются в виде квадратичной функции с параметрами (5). Расчет проведен на сетке М=50, N=40 (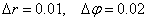 ) при
) при 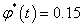 .
.
Как показывают расчеты, применение искусственной вязкости позволит значительно уменьшить амплитуду колебаний и при некоторых значениях коэффициентов 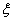 и
и 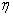 добиться полного их сглаживания.
добиться полного их сглаживания.
Литература:
1. Савурбаев А., Дангалов Н. А., Шертойлоков Г. М., Эшонкулов Ш. У. Алгоритм расчета переходного процесса при ударе цилиндрического кольца о жесткое полупространство. Молодой учёный. № 8 (67).июнь, 2014 г. с. 246–249.
2. Зенкевич О. Метод конечных элементов в технике. М., «Мир»,1975.
3. Рахматуллин Х. А., Сагомонян А. Я., Алексеев Н. А. Вопросы динамики грунтов. М. изд-во МГУ, 1964.







