Разработана методика проведения экспериментов по растяжению плоских круглых мембран нормальным давлением. Экспериментальные данные сопоставляются с результатами теоретических исследований. Для расчета эластомерных мембран предлагается использовать нелинейную теорию тонких оболочек.
Ключевые слова: эластомеры, экспериментальные данные, мембрана, деформации, напряжения, упругий потенциал.
Широкое применение в промышленности нашли такие конструкционные материалы, как эластомеры, обладающие нелинейными механическими свойствами. Изделия из них могут испытывать большие, до нескольких сотен процентов, деформации без разрушения. Соответственно, при расчете изделий из эластомеров используется нелинейная теория упругости [11–13, 15–17, 19]. Эластомеры применяются для изготовления мембран, оболочек, силовых и уплотнительных элементов. В расчетах нелинейная связь между напряжениями и деформациями здесь задается с помощью упругого потенциала. В теории тонких оболочек с использованием статической гипотезы Кирхгофа 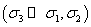 , закон упругости для несжимаемого материала принимает вид
, закон упругости для несжимаемого материала принимает вид
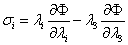
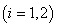 ,
,
где 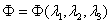 — упругий потенциал, являющийся для изотропного материала функцией кратностей удлинений
— упругий потенциал, являющийся для изотропного материала функцией кратностей удлинений 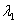 ,
, 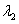 и
и 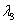 ,
, 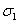 и
и 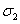 — напряжения, действующие в срединной поверхности. Для несжимаемого материала должно выполняться условие несжимаемости:
— напряжения, действующие в срединной поверхности. Для несжимаемого материала должно выполняться условие несжимаемости: 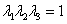 . На сегодняшний день предлагаемые в литературных источниках потенциалы строятся эмпирически на основе экспериментальных данных, а не на основе статистической теории. К числу таких потенциалов относятся потенциалы Муни — Ривлина, Бартенева — Хазановича, Джента — Томаса, Исихары, Бидермана, Александера, Харт — Смита, Огдена [15, 22]. Некоторые из них достаточно часто используются при решении конкретных задач [13, 15, 20–26, 29, 34, 39]. Ниже будет использоваться степенной потенциал, предложенный К. Ф. Черныхом (типа Огдена):
. На сегодняшний день предлагаемые в литературных источниках потенциалы строятся эмпирически на основе экспериментальных данных, а не на основе статистической теории. К числу таких потенциалов относятся потенциалы Муни — Ривлина, Бартенева — Хазановича, Джента — Томаса, Исихары, Бидермана, Александера, Харт — Смита, Огдена [15, 22]. Некоторые из них достаточно часто используются при решении конкретных задач [13, 15, 20–26, 29, 34, 39]. Ниже будет использоваться степенной потенциал, предложенный К. Ф. Черныхом (типа Огдена):
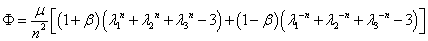 , (1)
, (1)
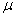 — линейный модуль сдвига,
— линейный модуль сдвига, 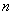 — параметр.
— параметр.
Из этого потенциала следуют потенциалы Бартенева-Хазановича (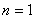 ,
,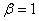 ), неогуковский (
), неогуковский (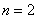 ,
, 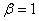 ), Муни-Ривлина (
), Муни-Ривлина (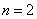 ). Теоретическое сопоставление этих потенциалов на основе экспериментальных данных проводилось в [15].
). Теоретическое сопоставление этих потенциалов на основе экспериментальных данных проводилось в [15].
Для определения механических характеристик эластомеров используются различные методики, основанные, как правило, на одноосном и двухосном растяжении образцов. Авторами работы были поставлены эксперименты по одноосному растяжению резиновых образцов в виде плоских мембран. В качестве испытуемых образцов брались полосы листовой резины различной марки (ГОСТ: ТУ 38.105.116–81, ТУ 38.305.05379–95) шириной от 55 мм до 120 мм, длиной от 150 мм до 400 мм, толщиной от 0.5 мм до 13 мм. Специально изготовленная установка технически позволяла растягивать образец длиною в 200 мм в 6 раз. При таких деформациях в окрестности зажимов в деформируемом образце напряженное состояние значительно отличается от однородного состояния. Состояние близкое к однородному реализуется в окрестности центральной части растянутого образца. В качестве базовой длины образца была принята длина в 200 мм. На недеформированный образец наносилась прямоугольная сетка (с квадратной ячейкой 5х5 мм) с помощью специально изготовленного для этих целей штампа для визуального контроля над искажением сетки на поверхности деформированного образца.
Образец зажимался в зажимы на краях, один край жестко закреплялся, а на втором прикладывалась нагрузка, растягивающая образец. При заданной нагрузке измерялось расстояние между «контрольными» метками, нанесенными на поверхность недеформированного образца на расстоянии 100 мм друг от друга. Нагрузка измерялась специально изготовленным динамометром. В общей сложности эксперименты по одноосному растяжению были проведены на 8 марках резин. Надо отметить, что остаточные деформации во всех экспериментах не превышали 1 %, т. е. для теоретического анализа можно использовать нелинейную теорию упругости. Характерная зависимость «нагрузка-деформация» для испытанных марок резин приведена на рис. 1 — символом  отмечены экспериментальные точки.
отмечены экспериментальные точки.
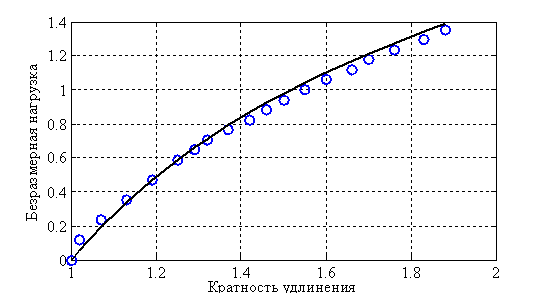
Рис. 1. Зависимость «безразмерная нагрузка — кратность удлинения» для одноосно растянутой резиновой полосы
Для упругого потенциала (1) зависимость «напряжение-деформация» в случае одноосного растяжения задается соотношением
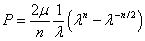 ,
,
где 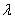 — относительное удлинение образца, значение параметра
— относительное удлинение образца, значение параметра 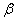 принималось равным единице. Экспериментальные данные аппроксимировались этой зависимостью с помощью метода наименьших квадратов. Для случая рис. 1 были получены следующие значения параметров:
принималось равным единице. Экспериментальные данные аппроксимировались этой зависимостью с помощью метода наименьших квадратов. Для случая рис. 1 были получены следующие значения параметров: 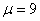 кг/см²,
кг/см², 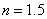 . Расчетной зависимости на рис. 1 соответствует сплошная линия. Для всех испытуемых образцов (8 марок резин) параметр
. Расчетной зависимости на рис. 1 соответствует сплошная линия. Для всех испытуемых образцов (8 марок резин) параметр 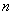 лежал в диапазоне от 1.2 до 1.8, а параметр
лежал в диапазоне от 1.2 до 1.8, а параметр 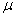 — от 1.5 до 100. Эти результаты согласуются с полученными в [15] данными.
— от 1.5 до 100. Эти результаты согласуются с полученными в [15] данными.
Для проведения экспериментов по растяжению плоских мембран была разработана методика их растяжения нормальным давлением и краевыми нагрузками, аналогичная предложенной в [15] для растяжения прямоугольных мембран. Растяжение мембран производилось по следующей схеме (рис. 2).

Рис. 2. Вид сбоку на установку, предназначенную для растяжения круглой мембраны нормальным давлением
В жёстком листе из оргстекла или металла вырезалось круглое отверстие. На жёсткую платформу, в которую вмонтировывались два металлических штуцера для подключения манометра и входного клапана, клалась листовая резина. Сверху устанавливался лист с вырезанным круглым отверстием. Платформа и лист с отверстием жёстко соединялись друг с другом. В данной методике для уменьшения эффекта «выползания» материала из «захватов» между листом резины и листом с отверстием устанавливался лист с отверстием из мелкой наждачной бумаги. Собранная конструкция устанавливалась на фоне стенки с масштабно-координатной сеткой. Через клапан (рис. 2) с помощью насоса небольшими порциями подавался воздух, который и создавал давление на мембрану. Для измерения давления использовались как циферблатный, так и водяной манометры. В процессе нагружения мембраны давлением велась съёмка цифровой камерой, по снимкам после компьютерной обработки цифровых изображений строилась форма мембраны при известном давлении. Фотосъёмка велась на расстоянии от 650 мм до 900 мм от стенки, а образец устанавливался на расстоянии около 110 мм от стенки с масштабно-координатной сеткой. Предлагаемый метод проведения экспериментального исследования по растяжению круглой мембраны нормальным давлением позволяет сопоставить результаты по одноосному растяжению с результатами по растяжению мембраны нормальным давлением для резин одной и той же марки из одного и того же «листового» материала.
Растяжению нормальным давлением подвергались «круглые» мембраны, изготовленные из листовой резины (толщина листов 1.2, 1.5 и 2 мм), что и в экспериментах по одноосному растяжению полос. Диаметры внутренних контуров 75 мм или 100 мм. На рис. 3 представлен вид на деформированную мембрану сбоку при разных значениях давления, отмеченных на рисунке цифрами (0.24 атм., 0.40 атм., 0.32 атм.).

Рис. 3. Вид на деформированную нормальным давлением круглую мембрану при различных давлениях (0.24 атм., 0.40 атм., 0.32 атм.)
На рис. 4 показана характерная зависимость «безразмерное давление-безразмерный прогиб в центре мембраны» — экспериментальные точки отмечены символом 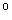 . В качестве «безразмерного прогиба» использовалось отношение прогиба мембраны в центре (
. В качестве «безразмерного прогиба» использовалось отношение прогиба мембраны в центре (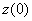 ) к радиусу опорного контура
) к радиусу опорного контура 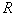 (
(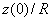 ), а в качестве давления — отношение произведения давления
), а в качестве давления — отношение произведения давления 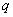 на радиус опорного контура к произведению модулю сдвига
на радиус опорного контура к произведению модулю сдвига 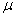 на толщину недеформированной мембраны
на толщину недеформированной мембраны 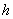 (
(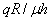 ). Во всех поставленных экспериментах зависимость «нагрузка-деформация» имела точку максимума. Точка максимума (рис. 4) достигалась практически сразу после выхода мембраны в окрестности зоны защемления за точки опорного контура (рис. 3,
). Во всех поставленных экспериментах зависимость «нагрузка-деформация» имела точку максимума. Точка максимума (рис. 4) достигалась практически сразу после выхода мембраны в окрестности зоны защемления за точки опорного контура (рис. 3, 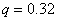 ).
).
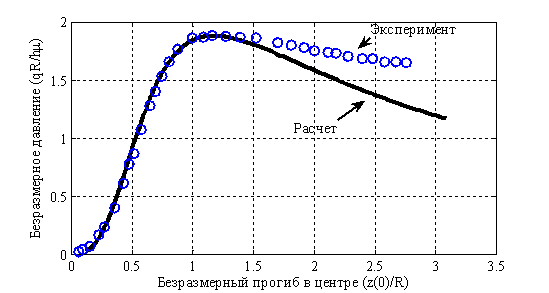
Рис. 4. Расчетная и экспериментальная зависимости «безразмерное давление – безразмерный прогиб» для круглой мембраны, растянутой нормальным давлением
В качестве моделей мембран и оболочек использовалась нелинейная безмоментная теория оболочек. Уравнения равновесия осесимметричной деформации оболочки вращения для случая нормального давления имеют следующий вид [13, 15]:
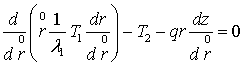 ,
,
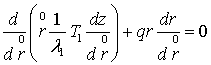 ,
,
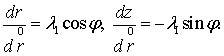
В этих соотношениях 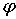 — угол между осью вращения и нормалью к срединной поверхности в деформированной конфигурации,
— угол между осью вращения и нормалью к срединной поверхности в деформированной конфигурации, 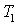 и
и 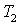 — усилия, действующие в срединной поверхности в меридиональном и окружном направлениях, а
— усилия, действующие в срединной поверхности в меридиональном и окружном направлениях, а 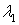 и
и 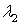 — кратности удлинений.
— кратности удлинений.
Связь между усилиями и кратностями удлинений для упругого потенциала (1) с 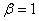 задается соотношениями
задается соотношениями
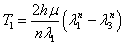 ,
, 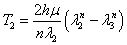 .
.
В качестве граничных условий рассматривались следующие:
при 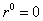 :
: 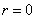 ,
, 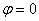 ;
;
при 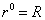 :
: 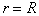 ,
, 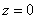 .
.
Предлагаемая система нелинейных уравнений решалась с применением двух алгоритмов, разработанных для решения краевых задач для нелинейных уравнений в частных производных [3–6, 14, 16, 18]. В одном случае осуществлялась дискретизация дифференциальных операторов конечными разностями. Полученная система нелинейных алгебраических уравнений решалась с применением метода простой итерации. В другом случае краевая задача сводилась к решению задачи Коши для системы обыкновенных дифференциальных уравнений. Полученные обоими методами теоретические результаты дали хорошее совпадение с экспериментальными. На рис. 2 расчетной зависимости (неогуковский потенциал, 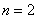 ) соответствует сплошная линия.
) соответствует сплошная линия.
Как следует из анализа экспериментальных и теоретических результатов по одноосному растяжению и двухосному растяжению нормальным давлением образцов, изготовленных из одного и того же «листового» материала, такие зависимости, как «напряжение-деформация» описываются различными потенциалами. Это можно объяснить тем, что внутренняя перестройка макромолекул образцов при одноосном и двухосном неоднородном напряженных состояниях происходит по разному. Возможно также, что по интегральным характеристикам типа «напряжение-деформация» для двухосного напряженного состояния строить упругий потенциал не вполне корректно. Вместе с этим теоретические результаты достаточно хорошо согласуются с экспериментальными результатами (рис. 4).
Физические свойства мембран могут быть и неоднородными — при их изготовлении могут возникать внутренние жесткие включения разного размера, внутренние микропоры и трещины, поверхностные дефекты. Решение математических задач с особенностями такого рода разработаны, для линейных уравнений теории упругости [1, 2, 7–10, 27, 28, 30–33, 35–37, 41]. Толщина в разных частях мембраны может быть разной. При больших деформациях искажения в напряженно-деформированном состоянии могут возникать и в зонах закрепления мембран. Неоднородности такого рода в нелинейной теории упругости, в отличие от линейной теории [10], практически, не исследовались. При расчете мембран, работающих в различных средах и при разных температурных режимах можно в первом приближении использовать методы расчета, разработанные [34, 38–40, 42, 43] в рамках линейной теории упругости.
Литература:
1. Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.
2. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. — 2014. — № 3 (62). — С. 1–6.
3. Гасратова Н. А., Бойцов Д. С., Габриелян Л. А., Тюганова Т. М. Математическая модель иммунного ответа организма млекопитающих на поражение кожи ожогом // Молодой ученый. — 2014. — № 12 (71). — С. 1–7.
4. Гасратова Н. А., Бойцов Д. С., Крылова В. А., Гаврилова А. В. Модель Базыкина-Свирежева хищник-жертва // Молодой ученый. — 2014. — № 12 (71). — С. 8–12.
5. Гасратова Н. А., Столбовая М. В., Бойцов Д. С., Степанова Д. С Математическая модель хищник-жертва на линейном ареале // Молодой ученый. — 2014. — № 11. — С. 1–10.
6. Гасратова Н. А., Столбовая М. В., Неверова Е. Г., Бербер А. С. Математическая модель «ресурс-потребитель» // Молодой ученый. — 2014. — № 10 (69). — С. 5–14.
7. Гасратова Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 101–106.
8. Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.
9. Даль Ю. М., Пронина Ю. Г. Деформация шаровой поры в нелинейно-упругом теле // Известия Российской академии наук. Серия физическая. — 2006. — Т. 70. — № 9. — С. 1341–1343.
10. Даль Ю. М., Пронина Ю. Г Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
11. Кабриц С. А. Мальков В. М., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
12. Кабриц С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала // Известия Российской академии наук. Механика твердого тела. — 2001. — № 1. — С. 38.
13. Кабриц С. А., Черных К. Ф. Нелинейная теория изотропно упругих тонких оболочек с учетом поперечного сдвига // Известия Российской академии наук. Механика твердого тела. — 1996. — № 1. — С. 124.
14. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226–232.
15. Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
16. Колпак Е. П. Mathlab: методы вычислений учебное пособие / Е. П. Колпак; Санкт-Петербургский гос. ун-т. Санкт-Петербург, 2007.
17. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
18. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4 (63). — С. 20–30.
19. Мальков В. М., Кабриц С. А., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
20. Мальков В. М., Малькова Ю. В. Анализ сингулярности напряжений в нелинейной задаче Фламана для некоторых моделей материала // Прикладная математика и механика. — 2008. — Т. 72. — № 4. — С. 652–660.
21. Мальков В. М., Малькова Ю. В. Исследование нелинейной задачи Фламана // Известия Российской академии наук. Механика твердого тела. — 2006. — № 5. — С. 68–78.
22. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для материала Бартенева-Хазановича // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 1–2. — С. 49–55.
23. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для несжимаемого материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 4. — С. 73–82.
24. Мальков В. М., Малькова Ю. В. Плоская задача нелинейной упругости для гармонического материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 3. — С. 114–126.
25. Мальков В. М., Малькова Ю. В. Плоские задачи о сосредоточенных силах для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 83–96.
26. Мальков В. М., Малькова Ю. В. Плоские задачи упругости для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 3. — С. 93–106.
27. Мальков В. М., Малькова Ю. В., Иванов В. А. Бесконечная плоскость с круговым включением, имеющим отслоение на части границы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 152–165.
28. Мальков В. М., Малькова Ю. В. Трещина в форме дуги окружности, расположенная вблизи поверхности раздела материалов // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2010. — № 1. — С. 93–104.
29. Мальков В. М., Малькова Ю. В., Степанова В. А. Двухкомпонентная плоскость из материала Джона с межфазной трещиной, нагруженной давлением // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2013. — № 3. — С. 113–125.
30. Пpонина Ю. Г. Оценка долговечности упpугой тpубы под действием пpодольной силы и давления в условиях pавномеpной повеpхностной коppозии // Деформация и разрушение материалов. — 2009. — № 2. — С. 41–45.
31. Пронина Ю. Г. Периодическая задача о точечных воздействиях в упругой полуплоскости с отверстиями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 3. — С. 118–128.
32. Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.
33. Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
34. Пронина Ю. Г Механохимическая коррозия полого цилиндра из идеального упруго-пластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2006. — № 3. — С. 121–130.
35. Пронина Ю. Г. Влияние поверхностных факторов на напряженно-деформированное состояние твердых тел с отверстиями // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербургский государственный университет. Санкт-Петербург, 2010.
36. Пронина Ю. Г. Краевая дислокация и сосредоточенная сила в упругой полуплоскости с отверстиями и краевыми вырезами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 4. — С. 120–124.
37. Пронина Ю. Г. О сосредоточенных воздействиях у границы упругой пластины // Труды ЦНИИ им. акад. А. Н. Крылова. — 2010. — № 53. — С. 117–122.
38. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
39. Пронина Ю. Г. Равномерная механохимическая коррозия полой сферы из идеального упругопластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2009. — № 1. — С. 113–122.
40. Пронина Ю. Г. Расчет долговечности упругой трубы под действием продольной силы, давления и осесимметричного нагрева в условиях равномерной коррозии // Проблемы прочности и пластичности. — 2009. — № 71. — С. 129–135.
41. Dal' Yu. M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57–60.
42. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
43. Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364.







