Рассмотрена причина возникновения ошибки, возникающей в результате выполнения преобразования в пространство лучей, применяемого к однородным кольцевым антенным решёткам (ОКАР). Исследован характер её зависимости при различных конфигурационных параметрах ОКАР. Приведены соответствующие зависимости.
Введение. Кольцевые антенные решётки (АР) находят свое применение в различных областях, например в таких как многоантенные коммуникационные передатчики, навигация и электронная разведка. Более того, однородная кольцевая антенная решётка (ОКАР) имеет одинаковые характеристики, не зависящие от углов прихода волн, излучённых источником радиоизлучения (ИРИ), и может одновременно оценивать углы азимута и места. Для того чтобы иметь возможность работать с вычислительно‑эффективными пеленгационными алгоритмами, к ОКАР применяется так называемый переход в пространство лучей. Он преобразует вектор отклика ОКАР к необходимой структуре Вандермонда, после чего для определения координат ИРИ могут быть применены методы, подобные алгоритму Root-MUSIC и ESPRIT [1], [2].
Преобразование в пространство лучей работает только при выполнении некоторых условий конфигурации АР, которые могут быть трудновыполнимы для некоторых практических приложениях. Например, когда используется ОКАР с малым количеством элементов (от шести до десяти), остаточная ошибка, вызванная преобразованием в пространство лучей, вносит смещение в оценки определения координат ИРИ.
Цель статьи — рассмотреть причины возникновения ошибки, вызванной переходом в пространство лучей и исследовать характер изменения её величины при различных конфигурационных параметрах ОКАР.
1. Модель сигнала
Рассмотрим ОКР, состоящую из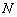 
антенных элементов. Предположим, что излучают 
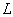источников 
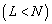. Передатчики излучают узкополосные сигналы с направлений 
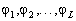, где 
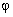— азимут. Более того предположим, что доступно 
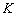выборок сигнала. Выходная матрица 
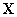размера 
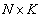может быть записана следующим образом:
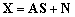(1)
где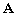 
— это матрица отклика ОКАР, размера 
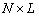пространстве элементов, 
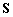–сигнальная матрица или матрица источников размера 
, 
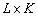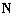— матрица шума, размера 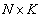. Шум смоделирован как стационарный, с нулевым средним, пространственный и временной белый комплексный гауссовский процесс. Матрица отклика в пространстве элементов для ОКАР записывается как 
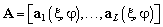, каждый вектор которой составлен из векторов
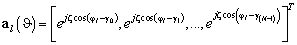(2)
для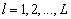 
. Здесь 
, 
, 
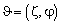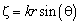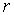— радиус решётки, 
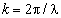волновое число, 
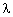— длина волны, 
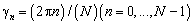— угловое положение антенных элементов. Угол места 
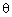измеряется вниз по оси 
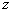. Азимут 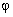измеряется против часовой стрелки по оси 
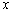; см. рисунок 1.
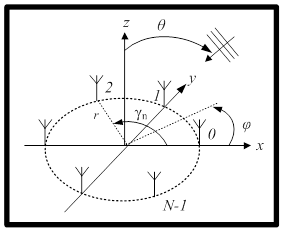
Рис. 1. ОКАР с 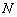элементами
2. Режим возбуждения фазовой моды
В этом разделе, рассматривается режим или принцип возбуждения фазовой модой [1], [2]. Сначала рассматривается непрерывная кольцевая апертура. Такая модель не может быть реализована на практике, но это самая подходящая конфигурация для применения принципа возбуждения фазовой моды, которая не приводит к появлению ошибок. Затем рассматривается дискретная АР, которую можно реализовать на практике.
2.A. Непрерывная кольцевая апертура
В случае непрерывной кольцевой апертуры, любая функция возбуждения является периодической по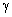 
с периодом 
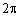и поэтому может быть представлена рядом Фурье [1], [2], [3]. Генерируемая функция возбуждения 
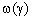может быть определена, используя обратное преобразование Фурье 
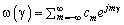, где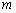 
‑ая фазовая мода 
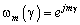представляется как пространственная гармоника возбужденной решётки, 
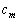— соответствующий коэффициент ряда Фурье, а 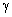представляет угловое положение точки, которая передвигается непрерывно в кольцевой апертуре.
Интегрируя пространственную гармонику возбуждённой решётки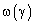 
по всей непрерывной кольцевой решётке, мы можем вычислить нормированную диаграмму направленности в дальней зоне 
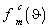, которая для 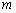‑ой фазовой моды вычисляется как [1], [2]:
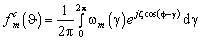(3)
Выражение (3) также может быть представлено с помощью функции Бесселя:
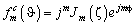(4)
где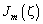 
— это функция Бесселя первого рода порядка .
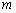Диаграмма направленности в дальней зоне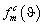 
имеет схожее с функцией возбуждения азимутальное отклонение 
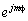. Это свойство позволяет использовать для синтеза диаграммы направленности режим возбуждения фазовой моды [1]. Вместо амплитудной и угломестной зависимости диаграммы направленности в дальней зоне она выражается через функцию Бесселя. Поэтому в данной кольцевой апертуре может возбуждаться только ограниченное число фазовых мод. Наивысший порядок моды 
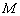— наименьшее целое число, максимально близко расположенное к 
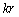. Таким образом, порядок мод будет 
.
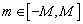2.Б. ОКАР
ОКАР — это случай решётки с непрерывной апертурой при конечном числе элементов решетки, равномерно распределённых по всей длине окружности; см. рисунок 1.
Для ОКАР, нормированный весовой вектор формирования луча, который возбуждает решётку фазовой модой 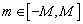[1], [2]:
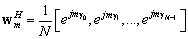(5)
где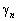 
— это угловое положение 
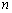‑го элемента, 
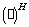знак эрмитова сопряжения. Тогда:
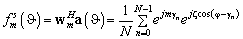(6)
где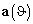 
— вектор отклика в пространстве элементов (2). Для моды порядка 
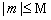, выражение (6) может быть переписано [1], [2]:
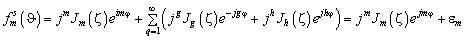(7)
где переменная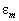 
отображает сумму, приведённую выше, а индексы 
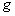и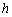 
определяются как 
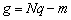и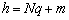 
.
Выражение (7) состоит из двух слагаемых. Первое слагаемое называется основной компонентой и идентично описанию диаграммы направленности решётки в дальней зоне для непрерывной антенной решётки. Второе слагаемое 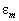называется остаточной компонентой, возникающей из‑за дискретизации непрерывной апертуры на 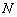элементов. Эта компонента известна как искажающая мода высокого порядка, порядок которой необходимо минимизировать для получения максимально приближенных к идеальным (непрерывной апертуре) характеристикам [2].
Обратите внимание, что, несмотря на то, что остаточная компонента 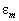представляет собой сумму из бесконечного количества элементов, только первый элемент, с индексом 
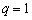, является значительным [1].
3. Анализ влияния параметров ОКАР на величину остаточной компоненты
Рассмотрим более детально выражения для остаточной компоненты (7). Очевидно, что она зависит от угла места и азимута. Следовательно, систематическая ошибка в оценках определения координат не является постоянной, а зависит от угла прихода сигнала. На рисунке 3 показана угловая зависимость остаточной компоненты как функци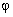и и 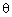. Значение 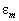уменьшается при изменении угла места с 
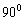до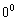 
, в то время как она ведет себя подобно синусоиде при изменении азимута.
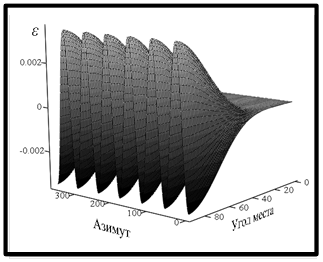
Рис. 2. Зависимость величины остаточной компоненты от координат ИРИ
Проанализируем поведение остаточной компоненты как функции различных параметрах конфигурации ОКАР. Очевидно, что чем ближе приближение к непрерывной апертуре, тем меньше становиться остаточная компонента. Принято, что остаточная компонента в (7) может рассматриваться как достаточно малая, если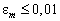 
[2].
На рисунке 3, отображена остаточная компонента как функция радиуса, для ОКАР с различным количеством элементов. Интересно отметить, что поскольку 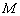пропорционально 
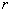(наименьшее целое число или эквивалентное 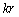), каждый раз, когда изменяется значение 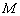, происходит скачок функции.
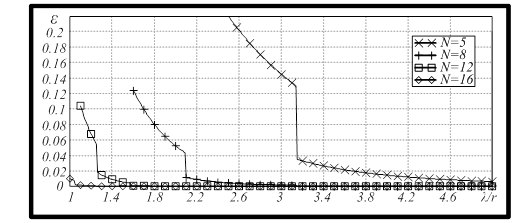
Рис. 3. Зависимость величины остаточной компоненты от радиуса ОКАР при различном количестве элементов
Из графиков, приведённых на рисунке 3, следует, что для фиксированного радиуса ОКАР, величина остаточной компоненты уменьшается при росте числа элементов ОКАР. Однако, при фиксированном количестве элементов, при увеличении радиуса, величина остаточной компоненты возрастает.
На рисунке 4 отображены численные результаты, показывающие зависимость остаточной компоненты от обоих параметров: числа элементов и радиуса решётки.
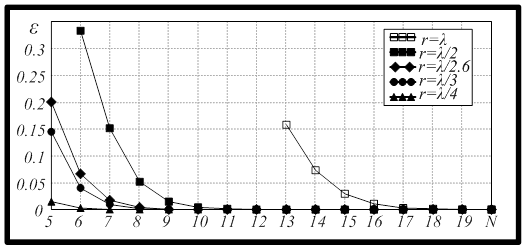
Рис. 4. Зависимость величины остаточной компоненты от количества элементов ОКАР при фиксированных значения радиуса
Из графиков, приведённых на рисунке 4, следует, что для фиксированного количества элементов решётки величина остаточной компоненты растёт при увеличении радиуса. Однако для фиксированного радиуса она уменьшается при увеличении количества элементов решётки.
Заключение. Применение вычислительно эффективных корреляционных алгоритмов пеленгования к ОКАР требует перехода в пространство лучей, который порождает ошибку, вызванную дискретной структурой ОКАР. Была рассмотрена причина возникновения ошибки, а также исследован характер её зависимости при различных конфигурационных параметрах ОКАР.
Литература:
1. C. P. Mathews and M. D. Zoltowski, “Eigenstructure techniques for 2‑D angle estimation with uniform circular arrays, ”IEEE Trans. Signal Process., vol. 42, no. 9, pp. 2395–2407, Sep. 1994.
2. F. Belloni and V. Koivunen, “Unitary root-MUSIC technique for uniform circular array,” in Proc. 3rd Int. Symp. Signal Process. Inf. Technol. (ISSPIT), Darmstadt, Germany, Dec. 14–17, 2003.
3. F. Belloni, A. Richter, and V. Koivunen, “Reducing excess variance in beamspace methods for uniform circular array,” in Proc. IEEE Work shop Statist. Signal Process. (SSP), Bordeaux, France, Jul. 17–20, 2005.
