Аннотация. В статье кратко описана методика учебного исследования явления интерференции волн от двух точечных источников с помощью компьютерной модели данного явления. Компьютерную программу, моделирующую интерференцию, предлагается использовать для объяснения результатов опыта Юнга.
Ключевые слова: визуализация, демонстрация явления, компьютерная визуализация, моделирование, компьютерное моделирование, модель, учебная компьютерная модель, физическая модель, предметная модель, интерференция, когерентные волны, опыт Юнга.
Моделированием называют такой метод познания, который подразумевает построение новых или выбор готовых моделей и изучение их в целях получения новых (в случае учебных моделей – субъективно новых) фактов и знаний об изучаемых объектах. В зависимости от того, что из себя представляют эти модели, научное моделирование может быть:
· предметным;
· мысленным;
· физическим;
· предметно-математическим;
· абстрактно-математическим (символьным).
Под предметным моделированием чаще всего понимают исследование характеристик объекта с помощью создания его уменьшенной копии с характеристиками, свойственными оригиналу. Это могут быть геометрические, физические, динамические, функциональные и другие свойства объекта. Мысленное моделирование осуществляется с помощью мысленных образов объекта, которые в определенных ситуациях могут вообще не иметь аналогов в реальном мире. Физическим моделированием в данном случае мы называем воспроизведение тех или иных физических процессов, протекающих в природе, в искусственно созданных условиях [1]. При предметно-математическом моделировании возможно проведение исследования, во время которого опытным путем изучается какой-либо объект физической природы, отличный от реально интересующего исследователя, но описываемый теми же математическими соотношениями, что и моделируемый объект. Абстрактно-математическое моделирование предполагает создание знаковых или символьных моделей, которыми могут являться формулы, схемы, чертежи и т. п. Процесс моделирования может быть автоматизирован с помощью вычислительной техники. В этом случае говорят о компьютерном моделировании [2; 3; 4; 5; 7; 8].
При обучении физике знания об объекте исследования могут быть усвоены обучающимися путем наблюдения за этим объектом и экспериментирования с ним. Но не всегда интересующие обучающего характеристики объекта легко поддаются выявлению и быстрому усвоению знаний о них обучающимися. Возникает методическая необходимость использовать при обучении не сам объект исследования, а его учебную модель. Учебная модель – это объект со своей структурой и функцией, отображающий некоторые элементы структуры и функции оригинала [11, с. 162]. Мы в своей работе используем учебные компьютерные модели, специально созданные нами для изучения обучающимися тех или иных физических явлений и процессов [2; 3; 4; 5; 7; 8; 9]. Эти модели представляют собой учебные модели (компьютерные программы), работа с которыми осуществляется с помощью компьютерной техники, которая в данном случае выполняет роль как устройства автоматизации вычислений, так и устройства, позволяющего визуализировать свойства объектов исследования, не поддающиеся непосредственному наблюдению [5; 6; 7; 8].
Рассмотрим, каким образом может быть организован учебный процесс по изучению явления интерференции с помощью компьютерной модели этого явления. Отметим, что данный компьютерный (вычислительный) эксперимент может сочетаться с учебным натурным экспериментом, подтверждающим те же положения теории явления интерференции [9; 10; 12]. Итак, при знакомстве обучающихся с явлением интерференции когерентных волн от двух точечных источников им демонстрируют следующую иллюстрацию (рис. 1), с помощью которой осуществляется вывод формулы, указывающей примерное расположение максимумов интерференционной картины вдоль прямой, параллельной отрезку, соединяющему источники. В результате использования некоторых приближенных математических выражений, которые мы опустим в этой работе, получается следующая формула, определяющая расположение максимумов интенсивности интерферируемой волны [9]:
xk,max = kyλ / d, k = 0, ±1, ±2, …,
где xk,max – координата максимума интенсивности, k – порядок максимума интенсивности, y – расстояние от источников до интерференционной картины (одномерного распределения интенсивности, представленного в виде графика), λ – длина волны, d – расстояние между источниками. Учитывая это, можно получить формулу, определяющую расстояние между соседними максимумами интерференционной картины [9]:
Δx = yλ / d.
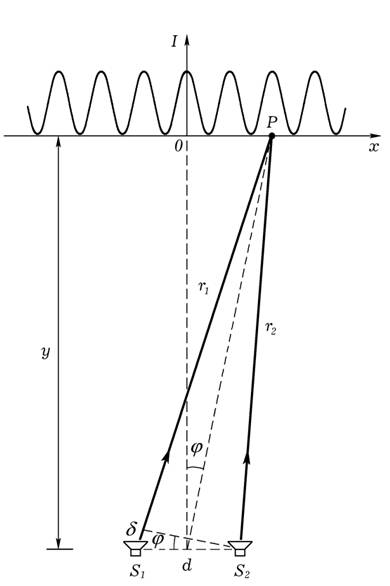
Рис. 1. Схема для расчета приближенной интерференционной картины от двух точечных источников волн
Вообще говоря, обучающиеся должны знать, что интерференционная картина в данном случае не является плоской или одномерной. При интерференции двух одинаковых сферических волн (а именно такими и будут волны от точечных источников) поверхностями равных разностей фаз являются гиперболоиды вращения с фокусами в точках расположения источников волн [2]. Иными словами, распределения характеристик интерферируемой волны будут четырехмерными (каждой точке распределения будут соответствовать три пространственные координаты и четвертый параметр – характеристика волны в этой точке). В таком виде визуализация распределений для учебных целей невозможна, так как слишком сложна для восприятия обучающимися. В этом случае в научной визуализации, как правило, используют такой известный прием, как снижение размерности [2]. Поэтому при создании моделирующей явление программы мы избавились в первом случае от одной, а во втором случае от двух пространственных координат, получив соответственно трехмерное и двумерное представления картины интерференции. Трехмерное представление распределения характеристик результирующей волны на координатной плоскости мы изображаем, сопоставив каждому значению характеристики интерферируемой волны в данной точке экрана соответствующий оттенок одного цвета, например, зеленого (светлые оттенки соответствуют большим значениям, темные – меньшим значениям). Такое распределение уже можно изобразить на экране для последующего анализа, причем его изображение будет двумерным, что делает его более понятным для обучающихся (рис. 2). Кроме того, на экран выводится распределение характеристики волны вдоль некоторой прямой, расположение которой задается пользователем программы. Оно размещается над первым распределением и позволяет осуществить количественную оценку исследуемого явления. В программе предусмотрено, что характеристиками волны могут выступать смещение, модуль смещения и интенсивность волны в данной точке пространства. Выбор характеристики, распределения которой выводятся в данный момент времени на экран, также осуществляется пользователем.
Предлагаемая нами программа предоставляет преподавателю возможность познакомить обучающихся с одним из современных методов исследования – компьютерным моделированием. При этом следует отметить, что при моделировании достаточно часто представляют интерес не абсолютные, а относительные значения величин, характеризующих моделируемый объект. В нашем случае, также, в первую очередь, для обучающихся будут важны относительные распределения смещения, модуля смещения и интенсивности волны на плоскости и вдоль прямой в волновом поле. А наиболее важным будет то, каково соотношение этих величин для рассматриваемых нами волн, то есть равны ли эти величины, а если не равны, то какая из них больше (или меньше) и во сколько раз [2]. Иными словами, моделирование в предлагаемой нами программе не связано с каким-то определенным типом волн, оно лишь отражает наиболее общие закономерности волновых явлений.
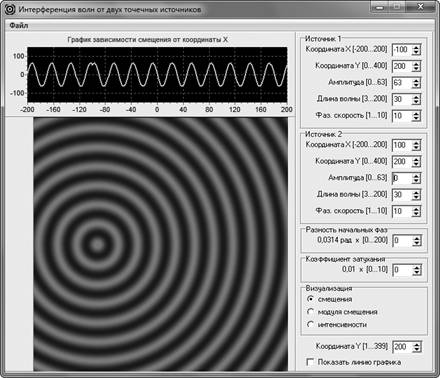
Рис. 2. Демонстрация волны от первого источника
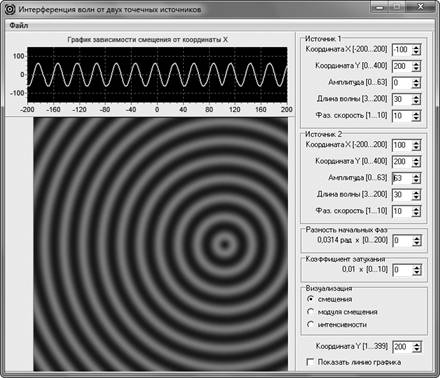
Рис. 3. Демонстрация волны от второго источника
Методика изучения явления с помощью компьютерного моделирования заключается в следующем. Сначала моделируют распределения смещения волны от первого источника (рис. 2). Выясняют, что моделируемая волна является сферической, так как наблюдается двумерное распределение, где линии равных фаз представляют собой окружности с центром в точке расположения источника волны. С помощью одномерного распределения (графика зависимости смещения от пространственной координаты) можно легко убедиться, что данная волна является еще и гармонической. После этого моделируют распределения смещения уединенной волны, распространяющейся от второго источника (рис. 3). Волна должна иметь ту же длину волны, как и та, что наблюдалась в первом случае. Отметив, что волны являются когерентными, преподаватель может создать проблемную ситуацию, задав вопрос о том, что будет наблюдаться, если обе эти волны будут распространяться в данном месте пространства одновременно при том же расположении источников волн. После дискуссии демонстрируется результат наложения волн (рис. 4). При этом важно обратить внимание на то, что между источниками когерентных волн возникла так называемая стоячая волна. Наблюдаемые динамические картины распределений смещения результирующей волны позволяют сформировать у учащихся наглядный образ явления интерференции.
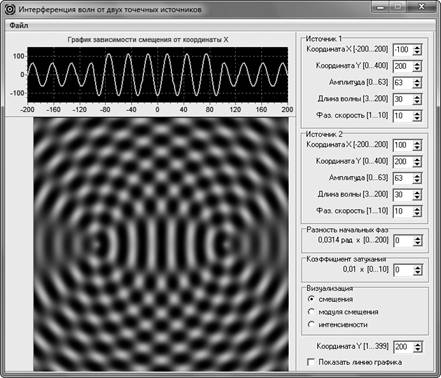
Рис. 4. Демонстрация наложения волн от двух источников
После этого моделируют распределение интенсивности результирующей волны (рис. 5). Такое моделирование помогает сформировать понятие интенсивности волны, как некоторой усредненной по времени характеристики, так как обучающиеся видят, что в случае демонстрации распределений интенсивности волны картины распределений становятся статичными. На этом этапе формируется понятие максимумов и минимумов интерференционной картины. Методика формирования этих понятий известна, поэтому приводить ее в этой статье мы не будем. Отметим только то, что сначала на экран выводится распределение интенсивности между источниками волн (рис. 5), а затем – расположенное на некотором удалении от них (рис. 6) [2].
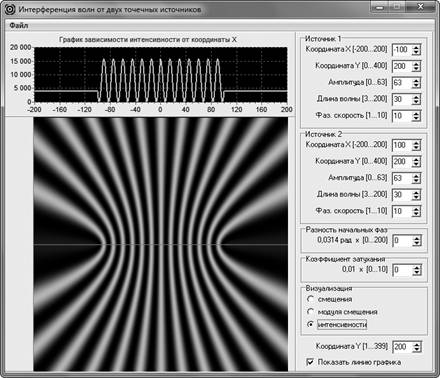
Рис. 5. Демонстрация интерференционной картины (распределений интенсивности результирующей волны вдоль отрезка прямой, соединяющего источники волн, и на плоскости)
В дальнейшем возможно исследование зависимости интерференционной картины (распределения интенсивности) от условий виртуального эксперимента. Следует отметить, что наблюдаемые графические картины распределений будут отличаться от картин, приведенных в учебниках. Это объясняется тем, что картины, изображенные в учебниках, получены аналитическим путем, когда считалось, что расстояние от источников до наблюдаемой интерференционной картины является «очень большим» по сравнению с расстоянием между источниками, в то время, как в рассматриваемых моделях оно соизмеримо с ним [2].
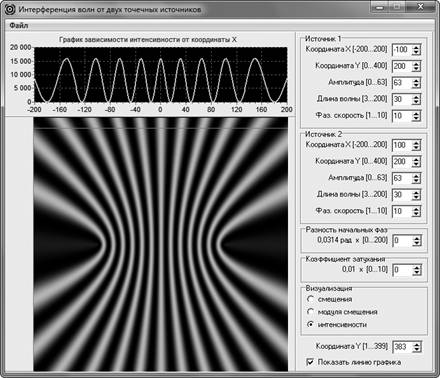
Рис. 6. Демонстрация интерференционной картины вдоль отрезка прямой, удаленного от источников волн на некоторое расстояние
ЛИТЕРАТУРА
1. Данилов О. Е. Изучение веса и невесомости с помощью модели упругого тела / О. Е. Данилов // Учебная физика. – 2001. – № 6. – С. 3-7.
2. Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2013. – № 9. – С. 50-58.
3. Данилов О. Е. Компьютерное моделирование движения молекул газа / О. Е. Данилов // Проблемы учебного физического эксперимента: Сборник научных и методических работ. Выпуск 2. – Глазов: ГГПИ, 1996. – С. 78-80.
4. Данилов О. Е. Компьютерное моделирование колебательного движения. Численные методы решения задач: учебно-методическое пособие / О. Е. Данилов, А. Ю. Трефилова. – Глазов: Глазов. гос. пед. ин-т, 2012. – 36 с.
5. Данилов О. Е. Обучение компьютерному моделированию на примере создания компьютерной модели кругового математического маятника / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2013. – № 10. – С. 80-87.
6. Данилов О. Е. Педагогические исследования по доказательству эффективности применения метода компьютерного сканирования полей при обучении физике / О. Е. Данилов // Инновации в образовании. – 2014. – № 6. – С. 147-158.
7. Данилов О. Е. Применение имитационного моделирования механических взаимодействий при обучении физике / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2014. – № 5. – С. 97-103.
8. Данилов О. Е. Учебная компьютерная модель дифракции / О. Е. Данилов // Теория и практика образования в современном мире: материалы IV междунар. науч. конф. (г. Санкт-Петербург, январь 2014 г.). – СПб.: Заневская площадь, 2014. – С. 198-199.
9. Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2013. – № 7. – С. 84-94.
10. Данилов О. Е. Экспериментальное изучение интерференции звука на зеркале Ллойда с помощью компьютерных технологий / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2014. – № 4. – С. 89-94.
11. Смирнов А. В. Методика применения информационных технологий в обучении физике: учеб. пособие для студ. высш. пед. учеб. заведений / А. В. Смирнов. – М.: Издательский центр «Академия», 2008. – 240 с.
12. Danilov O. Particular didactic principles on the use of computer visualization of the fields of physical quantities in the educational process / O. Danilov // Young Scientist USA: Education. – Lulu, 2014. – P. 29-32.







