Работа посвящена задаче реконструкции трехмерных сцен по стереоизображениям. Предложена модель сопоставления изображений с учетом эпиполярных ограничений, которая позволяет избежать процедуры ректификации, вносящей дополнительные искажения.
Ключевые слова: модель, стереоизображения, эпиполярная геометрия
Задачей настоящей работы является построение модели реконструкции 3D сцен, позволяющей избежать проективных преобразований стереоизображений до начала этапа поиска соответствующих точек. Данная модель является обобщением методов и алгоритмов, предложенных автором в работах [1–4]. Эта модель должна предусматривать возможность поиска соответствующих точек непосредственно на исходных стереоизображениях. Построение такой модели связано с двумя принципиально важными аспектами проблемы.
Эпиполярные линии на стереоизображениях описываются уравнением прямой, поэтому координаты соответствующих точек на них — вещественные числа. В то же время соответствующие фрагменты на стереоизображениях характеризуются функциями распределения яркости на дискретном множестве отсчетов изображений и могут быть определены лишь с точностью до величины межпиксельного расстояния. В связи с указанной проблемой в рамках общей модели учета эпиполярных ограничений возникают следующие две задачи.
1. Разработка метода и численного алгоритма поиска соответствующих фрагментов с дискретными отсчетами яркостей изображений на стереоизображениях с использованием множества заданных на эпиполярных прямых точек, имеющих вещественные координаты.
2. Разработка и исследование вычислительной схемы поиска соответствующих фрагментов в некоторой окрестности эпиполярной линии путем учета близости этого фрагмента к ней.
В первом случае мы предполагаем реализацию схемы, в которой сначала задается некоторое множество точек с вещественными координатами на эпиполярных прямых, и для этих точек подбираются наиболее подходящие соответствующие фрагменты изображений с использованием специально формируемых для этой цели дескрипторов. Во втором случае наиболее «похожие» соответствующие фрагменты подбираются в некоторой окрестности эпиполярных линий с учетом их близости к эпиполярным линиям.
В обоих случаях для реализации указанных схем учет эпиполярных ограничений должна быть известна фундаментальная матрица. Если известны параметры камер, фундаментальная матрица может быть вычислена точно. Если параметры камер не известны, эта матрица может быть оценена по соответствующим точкам на этих же стереоизображениях.
Общая модель реконструкции трехмерных сцен с учетом эпиполярных ограничений строится следующим образом. Предполагается, что заданы два стереоизображения: 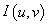 ,
, 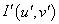 заданных размеров. Каждый отсчет (пиксел) изображения имеет целочисленные координаты u и v и характеризуется значением яркости. Для указанной пары изображений считаются известными (заданными):
заданных размеров. Каждый отсчет (пиксел) изображения имеет целочисленные координаты u и v и характеризуется значением яркости. Для указанной пары изображений считаются известными (заданными):
1) Фундаментальная матрица 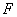 (или уравнения эпиполярных линий) и определяемые ими допустимые множества точек
(или уравнения эпиполярных линий) и определяемые ими допустимые множества точек 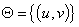 ,
, 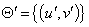 , среди которых ищутся соответственные, где
, среди которых ищутся соответственные, где 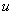 ,
, 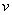 ,
, 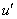 и
и 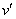 — координаты этих точек.
— координаты этих точек.
2) Правило формирования окрестностей (фрагментов изображений) 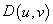 и
и 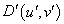 для точек
для точек 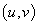 ,
, 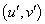 из допустимого множества в виде множества целочисленных отсчетов и критерий близости
из допустимого множества в виде множества целочисленных отсчетов и критерий близости
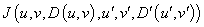 (1)
(1)
этих фрагментов.
Задача сопоставления изображений состоит в поиске соответствующей точки 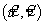 для точки
для точки 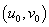 путем решения задачи минимизации:
путем решения задачи минимизации:
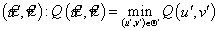 , (2)
, (2)
где
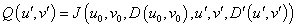 . (3)
. (3)
Эта модель может иметь различные формы в зависимости от способа реализации п. 1 и 2 модели. Рассмотрим некоторые частные случаи реализации эпиполярных ограничений.
Основное эпиполярное ограничение записывается в виде равенства (4)
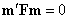 . (4)
. (4)
Это соотношение можно также представить в виде:
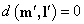 , (5)
, (5)
где 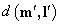 — расстояние от точки
— расстояние от точки 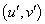 до эпиполярной прямой
до эпиполярной прямой 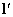 , соответствующей точке
, соответствующей точке 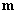 :
:
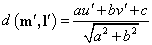 (6)
(6)
(здесь 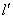 представлена как
представлена как 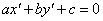 ). Учет эпиполярных ограничений может быть осуществлен, по крайней мере, двумя различными способами.
). Учет эпиполярных ограничений может быть осуществлен, по крайней мере, двумя различными способами.
Ограничение в виде равенства:
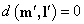 . (7)
. (7)
Это равенство накладывает строгое условие на соблюдение эпиполярных ограничений. В большинстве случаев, данное требование может быть выполнено только в случае вещественных координат сопоставляемых точек. Кроме того, фундаментальная матрица в этом случае должна быть вычислена точно.
Ограничение в виде неравенства:
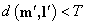 . (8)
. (8)
Это ограничение создает «полосу» вдоль эпиполярной линии, внутри которой может быть найдена соответственная точка. Этот способ учета эпиполярных ограничений требует выбора порога, что может представлять некоторые трудности.
Эпиполярные ограничения могут также задаваться в виде требования близости к эпиполярной линии. Учет этих требований может быть реализован, например, в виде весового коэффициента штрафа:
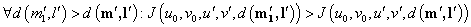 . (9)
. (9)
В этом случае величина критерия зависит от величины расстояния от точки до эпиполярной линии. При этом зависимость должна быть монотонно возрастающей. В данном случае наиболее подходящей является форма записи эпиполярного ограничения в виде соотношений (5), (6). В этом представлении величина «невязки» не зависит от абсолютных координат выбранных точек, в отличие от исходного способа записи (4).
Вид используемого критерия и способы реализации эпиполярных ограничений, в свою очередь, определяют способ восстановления трехмерной модели. Далее рассмотрим два способа определения координат точек сцены в рамках предложенной модели. Вначале рассмотрим случай, когда соответствующие точки 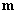 и
и 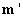 на стереопаре изображений левого и правого вида соответственно точно принадлежат эпиполярным линиям. Ясно, что при этом их координаты, скорее всего, будут вещественными (не целыми) числами.
на стереопаре изображений левого и правого вида соответственно точно принадлежат эпиполярным линиям. Ясно, что при этом их координаты, скорее всего, будут вещественными (не целыми) числами.
Рассмотрим первый вариант учета эпиполярных ограничений, когда для заданных точно на эпиполярных прямых точек подбираются наиболее похожие дискретные окрестности. Для начала формально запишем все элементы метода, входящие в предложенную модель.
1) Множества сопоставляемых точек 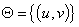 и
и 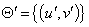 представляют собой набор точек, выбранных с фиксированным шагом на соответствующих эпиполярных линиях. Множество эпиполярных линий задается таким образом, чтобы получить «облако» точек восстанавливаемой сцены с требуемым разрешением.
представляют собой набор точек, выбранных с фиксированным шагом на соответствующих эпиполярных линиях. Множество эпиполярных линий задается таким образом, чтобы получить «облако» точек восстанавливаемой сцены с требуемым разрешением.
2) В качестве окрестности для каждой вещественной точки 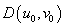 выбираются вершины единичного квадрата, внутрь которого попадает эта точка.
выбираются вершины единичного квадрата, внутрь которого попадает эта точка.
3) В качестве дескриптора выступает интерполированная яркость и интерполированные градиенты по направлениям, рассчитанные по окрестности выбранной точки.
4) Критерий качества 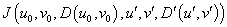 задается в виде нормы разности соответствующих дескрипторов по сопоставляемым точкам и соседним с ними, расположенным на той же эпиполярной прямой.
задается в виде нормы разности соответствующих дескрипторов по сопоставляемым точкам и соседним с ними, расположенным на той же эпиполярной прямой.
5) Эпиполярные ограничения в задаче минимизации учитываются в виде равенства (7), т. е. соответствия устанавливаются только между точками, расположенными на соответствующих эпиполярных прямых.
Вычислительный алгоритм, выполняемый при указанных условиях, реализован и исследован в работах автора [1–3].
В ситуации, когда направления эпиполярных линий примерно одинаковы, что характерно, например, для космических стереоизображений, более подходящим является второй способ учета эпиполярных ограничений. При этом принимаются во внимание следующие условия.
1) Множество сопоставляемых точек 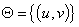 и
и 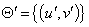 представляет собой множество дискретных отсчетов на изображениях в окрестностях эпиполярных линий, определяемых неравенством (8).
представляет собой множество дискретных отсчетов на изображениях в окрестностях эпиполярных линий, определяемых неравенством (8).
2) В качестве сопоставляемого фрагмента изображения 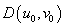 для точки
для точки 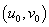 принимается область вокруг этой точки с заданными фиксированными размерами и формой.
принимается область вокруг этой точки с заданными фиксированными размерами и формой.
3) Дескриптором для точки 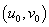 является множество значений яркостей отсчетов из области
является множество значений яркостей отсчетов из области 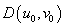 в окрестности этой точки.
в окрестности этой точки.
4) Критерий 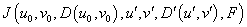 представляет собой меру сходства двух фрагментов, которая учитывает значения координат, интенсивностей отсчетов, а также близость точки к соответствующей эпиполярной линии.
представляет собой меру сходства двух фрагментов, которая учитывает значения координат, интенсивностей отсчетов, а также близость точки к соответствующей эпиполярной линии.
В условиях 1 и 4 содержатся эпиполярные ограничения, задаваемые соотношением (8), а также накладывается требование близости к эпиполярной линии. Вычислительный алгоритм, соответствующий указанным условиям, исследован автором в работе [4].
Использование предложенной модели реконструкции позволяет избежать применения в явном виде ректификации и связанных с ней искажений изображений. Вместе с тем, эпиполярные ограничения, задающие решение в одной плоскости позволяют получить достаточно высокое качество реконструкции сцены
Автор выражает благодарность научному руководителю, д.т.н., профессору Фурсову В. А. за помощь при подготовке настоящей работы и ряд важных замечаний. Работа выполнена при поддержке РФФИ (проекты № 12–07–00581, № 13–07–12030 офи_м, № 13–07–13166).
Литература:
1. Гошин Е. В. Реконструкция 3D-сцен на пучках эпиполярных плоскостей стереоизображений / В. А. Фурсов, С.А Бибиков, Е. В. Гошин // Мехатроника, Автоматизация, Управление — М., № 9(150), 2013. — C. 19–24.
2. Гошин Е. В. Реконструкция 3D-сцен по неректифицированным стереоизображениям с прореживающей фильтрацией / В. А. Фурсов, Е. В. Гошин // «Известия Самарского научного центра РАН» — М., № 9(150), 2013. — C. 19–24.
3. Goshin Ye.V. 3D Scene Reconstruction From Unrectified Stereo Images / V. A. Fursov, Ye.V. Goshin // 11th International Conference on Pattern Recognition and Image Analysis: New Information Technologies (PRIA-11–2013). — 2014. — С. 190–193.
4. Гошин Е. В. Информационная технология реконструкции цифровой модели местности по стереоизображениям / В. А. Фурсов, С.А Бибиков, Е. В. Гошин // Компьютерная оптика — Самара, Том 38, № 2, 2014.. — C. 19–24







