Осуществляется параметрическая идентификация транспортно-логистической компании как системы массового обслуживания (многокритериальная система). Определяются основные характеристики процессов обслуживания, а также производится оценка качества функционирования всей обслуживающей системы. Приводится иллюстрация на примере системы с заданными параметрами.

Ключевые слова: перевозка грузов, транспортно-логистическая компания, система массового обслуживания, многокритериальная оптимизация.

Организация функционирования обслуживающей системы одними качественными методами принципиально невозможна и требует применения количественных методов решения. Только количественные методы позволяют обоснованно судить о том, что данный способ организации лучше или хуже другого, что данная обслуживающая система справляется с обслуживанием лучше всех возможных и т. д. Во многих случаях оценка их деятельности может производиться методами, широко используемыми в теории систем массового обслуживания (отыскание основных характеристик процессов обслуживания; оценка качества функционирования всей обслуживающей системы; разработка математических методов и др.). Так, в задачах автосервиса такие методы используются для определения среднего числа машин, нуждающихся в ремонте в данный момент; установления числа автомашин, выходящих из строя за определенный промежуток времени (зависит от времени года, от состояния дорог в данном районе, от квалификации водителей, соблюдения графиков профилактических осмотров и ряда других случайных факторов). Поэтому необходимо знать их вероятностные характеристики [1…6]. Существенным является определение числа требований (несправных машин), которое может быть и очень большим. Поток требований, нуждающихся в обслуживании и поступающих в обслуживающую систему, рассматривается как входящий в систему поток;покидающий обслуживающую систему — как выходящий (требования, поступающие в обслуживающую систему, могут покидать ее и не обслуженными).

Аналогичные задачи возникают и при оценке деятельности транспортно-логистических компаний (оптимизация транспортных издержек; оптимизация маршрутов перевозки грузов; расчет транспортных расходов; организация и обеспечение доставки товаров, экономическое обоснование вариантов доставки, независимо от объема груза и др.), которые рассмотрим более подробно.

Так, пусть автотранспортная компания имеет в своем распоряжении 5 автомашин и обеспечивает круглосуточную срочную доставку грузов (при ограниченном числе заявок на доставку; отказ в обслуживании при количестве заявок >10 (максимальная длина очереди — 10; прием заявок прекращается пока не будет обслужена одна очередная заявка, и очередь уменьшится)). Поток заявок предполагается простейшим, среднее количество заявок в час 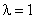. Вероятность поступления ровно  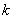заявок за время :

.

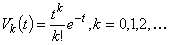При показательном законе распределения времени доставки груза (время обслуживания; зависит: от того, где находится груз, куда его необходимо доставить, вида груза, времени суток, качества дороги и т. д.) параметр 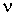 будет равен единице, если на удовлетворение одной заявки требуется один час.

Определим показатели работы компании (вероятность того, что все машины заняты; среднюю длину очереди и др.). Здесь требованием на обслуживание является заявка на доставку груза; обслуживающий аппарат — автомашина; обслуживание — доставка груза; число обслуживающих аппаратов системы (компании) 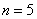, максимальная длина очереди 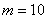; наибольшее число заявок обслуживаемых и ожидающих обслуживания .

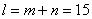Вероятность того, что все машины заняты, есть

;

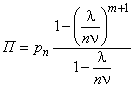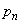 — вероятность того, что занято точно  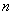обслуживающих аппаратов при условии, что общее число требований, находящихся на обслуживании не превосходит числа обслуживающих аппаратов, определяется (при 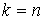) в соответствии с

, ;

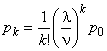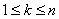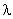- среднее число требований, поступающих в систему за единицу времени;

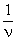 — среднее время обслуживания одной автомашиной одного требования;

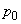 — вероятность того, что все обслуживающие машины свободны,

;

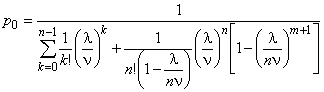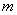 — наибольшая допустимая длина очереди;

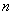 — число обслуживающих автомашин.

С учетом 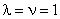,  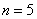получим

;

.

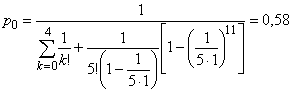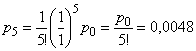Имеем

;

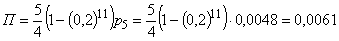вероятность полной загруженности компании мала.

Качество обслуживания определится средней длиной очереди (среднее число требований, ожидающих начало обслуживания)

;

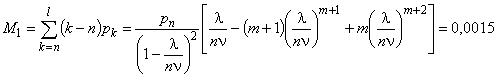практически очереди не будет.

Таким образом, при выбранных значениях (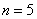,,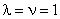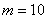) заказчик практически не получит отказа в обслуживании, однако и загрузка машин будет незначительна (задаваясь иными значениями 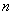,,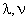, 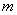можно скорректировать работу компании в необходимом направлении).

Литература:

1.      Данилов А. М., Гарькина И. А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. — Пенза: ПГУАС. –2014. — 168 с.

2.      Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.

3.      Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие. — Пенза: ПГУАС. — 2010. — 228 с.

4.      Гарькина И. А., Данилов А. М., Королев Е. В., Смирнов В. А. Преодоление неопределенностей целей в задачах многокритериальной оптимизации на примере разработки сверхтяжелых бетонов для защиты от радиации / Строительные материалы — Наука. — 2006. — № 8. — С.23–26.

5.      Гарькина И. А., Данилов А. М., Петренко В. О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. –2013. –№ 2 (41). –С. 123–129.

6.      Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. –2013. –№ 5. –С. 42–45.