В статье рассмотрена нестационарная пространственно-двумерная модель транспорта наносов в прибрежной зоне водоемов, учитывающая следующие физические параметры и процессы: пористость грунта, критическое значение касательного напряжения, при котором начинается перемещение наносов, турбулентный обмен, динамически изменяемую геометрию дна и функцию возвышения уровня, ветровые течения, трение о дно. Выполнена дискретизация предложенной модели транспорта наносов. Показано, что построенные разностные схемы обладают первым порядком погрешности аппроксимации относительно шага по временной переменной и вторым — относительно шагов по пространственным переменным.
Ключевые слова: транспорт наносов, разностные схемы, аппроксимация, погрешность.
Введение. При конструктивном преобразовании рельефов следует учитывать динамику процессов образования берега, исследовать формирование профиля дна в прибрежных акваториях под воздействием волновых процессов. Процесс перемещения наносов волнового поля вдоль берега относят к одному из важнейших явлений прибрежной зоны водоема [1, 2].
Для достоверного прогноза динамических явлений береговой зоны возникает необходимость в построении математических моделей процессов переноса вещества на мелководье под воздействием поверхностных гравитационных волн, играющих важную роль в прогнозировании возможного вмешательства в экосистему, в анализе текущей ситуации, в принятии оперативных решений по преодолению антропогенных воздействий [2, 4].
Одним из наиболее эффективных методов исследования реальных процессов гидродинамики в настоящее время является численное моделирование. Для задач математического моделирования гидродинамических процессов в водоемах актуальной остается проблема построения и практического использования вычислительно-эффективных методов, применение которых позволяло бы получать достаточно точное приближенное численное решение. Математическое моделирование природных систем, в том числе мелководных водоемов, дополняет, а во многих случаях позволяет исключить дорогостоящие натурные эксперименты с реальной экосистемой [4, 5, 6].
Непрерывная модель. Уравнения процесса перемещения наносов запишем в дивергентном виде [7, 8]: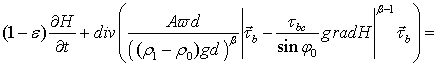 
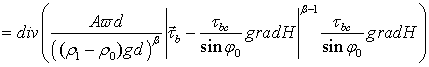. (1)
где Н — глубина дна, отсчитываемая от невозмущенной поверхности водоема; 
‒ пористость грунта; x, y — горизонтальные декартовы координаты;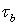 
‒ касательное напряжение на дне; 
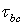‒ критическое значение касательного напряжения, при котором начинается перемещение наносов; А и 
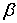— безразмерные постоянные (в настоящей работе А равна 19,5, 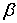равна 3), 
‒ частота волны; d ‒ характеристика осадков; 
— плотности твердых частиц и воды;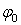 
— угол естественного откоса грунта в воде; 
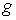— ускорение свободного падения; 
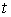— время.
Введем обозначение: 
С учетом ограничений на касательные напряжения на дне расчетной области данное выражение запишем в виде [5, 9]: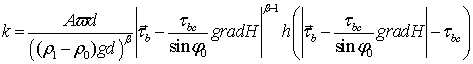 
, (2)
где 
— функция Хэвисайда.
Записав уравнение (1) с учетом (2), имеем:
(3)
Уравнение (3) дополним начальным условием: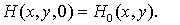 
(4)
На границе отсутствует поток, вызванный влиянием гравитационных сил:
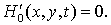(5)
Таким образом, имеем непрерывную двумерную математическую модель формирования наносов в прибрежной зоне водоема (1)-(5).
Дискретизация двумерной математической модели транспорта наносов. Следующим этапом разработки двумерной математической модели процессов перемещения наносов в прибрежной зоне является построение дискретной модели по непрерывному аналогу. Построим разностную схему, аппроксимирующую уравнение (3) с соответствующими граничными и начальными условиями (4)-(5).
Расчетная область вписана в прямоугольник. Покроем область равномерной прямоугольной расчетной сеткой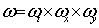 
[10, 11]:
,
,
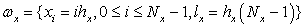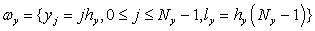где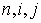 
— индексы по временной координате и пространственным координатным направлениям 
,
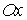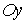соответственно; 
— шаги по временной координате и пространственным координатным направлениям 
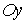соответственно; 
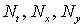— количество узлов по временной координате и пространственным координатным направлениям 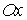, 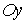соответственно; 
— длина расчетной области по временной координате и пространственным координатным направлениям 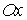, 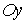соответственно.
Для получения дискретной модели воспользуемся интегро-интерполяционным методом [11, 12]. Для этого запишем уравнение (3) в следующем виде:
, (6)
где 
Интегрируя уравнение (6) по области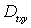 
:
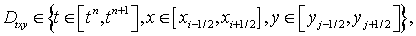имеем:
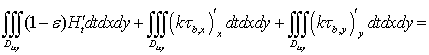
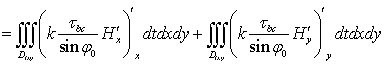. (7)
Вычислим каждый из полученных интегралов в отдельности.
Найдем значение первого интеграла, стоящего в левой части уравнения (7):
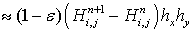, где 
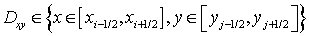. (8)
Найдем значение второго интеграла, стоящего в левой части уравнения (7):
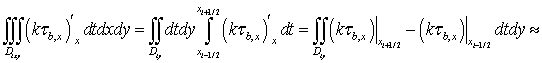
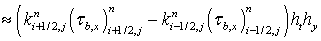. (9)
Аналогичным образом можно записать значение третьего интеграла, стоящего в левой части уравнения (7):
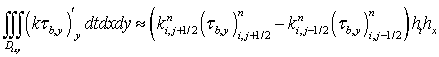. (10)
Найдем значение первого интеграла, стоящего в правой части уравнения (7):
. (11)
Обозначим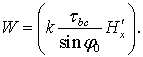 
Проинтегрируем выражение на отрезке 
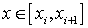, имеем: 
. (12)
Левую часть равенства (10) запишем в виде: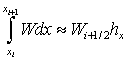 
.
Преобразуем правую часть выражения (12):
.
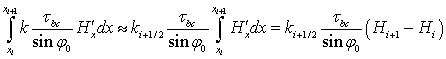Таким образом, выражение (12) можно записать в виде:
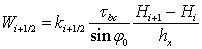. (13)
Подставим (13) в (12), в результате получим:
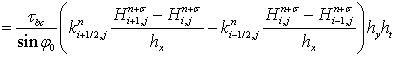, (14)
где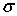 
— вес схемы [13].
Аналогично получим значение второго интеграла, стоящего в правой части уравнения (7):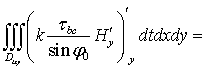 
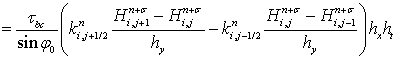. (15)
Подставив выражения (8)-(10), (14)-(15) в уравнение (7), имеем:
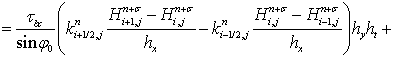
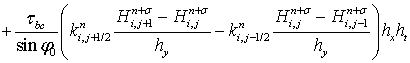. (16)
Разделив выражение (16) на 
, получим дискретную модель транспорта наносов:
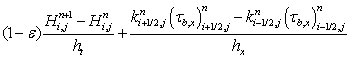
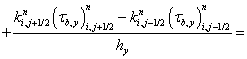
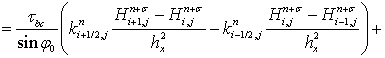
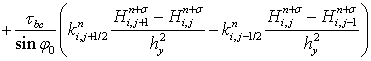, (17)
где 
, 
,
Найдем значение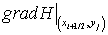 
. Обозначим 
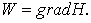Проинтегрируем данное выражение по области 
: 
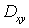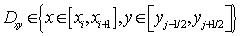, в результате получим: 
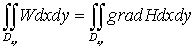. (18)
Левую часть данного выражения запишем в виде: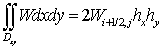 
.
Правую часть выражения (18) запишем в виде:
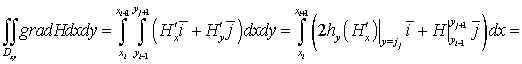
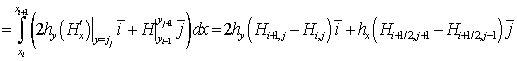
Таким образом, выражение (18) можно записать в следующем виде:
, (19)
где 
— единичные вектора, направленные вдоль координатных осей 
соответственно.
Аналогичным образом можно получить следующую аппроксимацию:
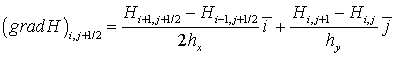. (20)
Таким образом, уравнение (17) с аппроксимациями (18)-(19) задают дискретную модель транспорта наносов.
Погрешность аппроксимации конечно-разностной схемы. Найдем погрешность аппроксимации дискретной модели транспорта наносов. Запишем следующие разложения в ряд Тейлора относительно точки 
с координатами 
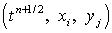[10, 12].
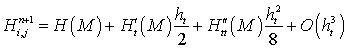, (21)
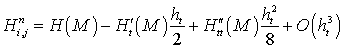. (22)
При помощи разложений (21)-(22) можно вычислить порядок погрешности аппроксимации первого слагаемого в дискретной математической модели транспорта наносов (17).
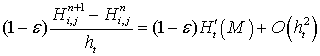. (23)
Для расчета погрешностей оставшихся слагаемых модели трансорта наносов (17) понадобятся разложения в ряд Тейлора относительно точки 
,
.
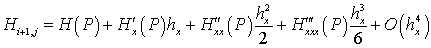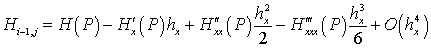Найдем погрешность аппроксимации для следующего выражения:
.
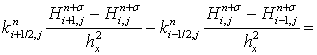
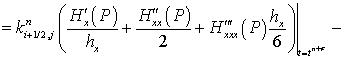
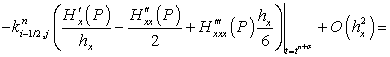
Принимая во внимание следующие равенства:
,
, получим:
.
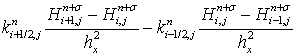
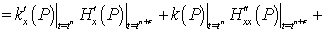
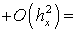
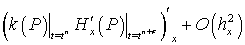Таким образом, 
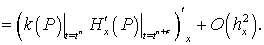(24)
Найдем погрешность аппроксимации для следующего оператора:
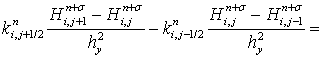
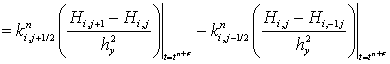
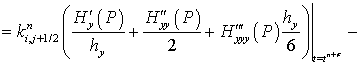
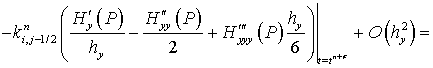
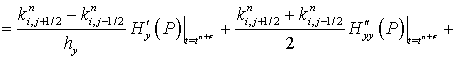
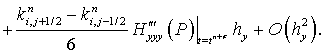
Принимая во внимание следующие равенства:
получим:
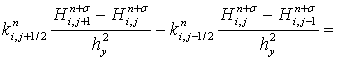
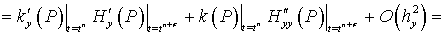
(25)
Таким образом, погрешность аппроксимации данного оператора 
Нетрудно убедиться, что выражения (24) и (25) обладают вторым порядком погрешности аппроксимации по пространственной координате.
В результате получим следующее выражение:
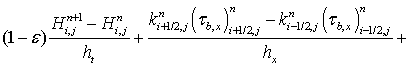
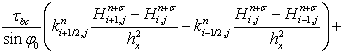
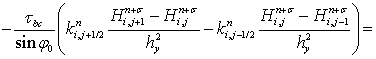
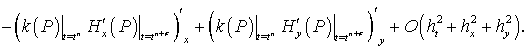
Принимая во внимание следующие равенства:
, 
,
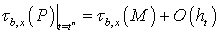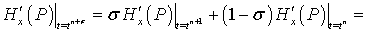
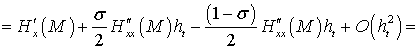
, получим первый порядок погрешности аппроксимации по временной переменной.
Повышение порядка погрешности дискретизации до второго по времени приводит к необходимости решения систем нелинейных уравнений, что негативно сказывается на скорости вычисления. Следует также отметить, что кроме выражений 
, 
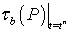все остальные операторы аппроксимированы со вторым порядком погрешности аппроксимации при условии 
.
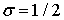Вычислим погрешность аппроксимации коэффициентов 
.
Для этого найдем погрешность дискретизации поля градиента глубины в точках 
и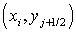 
. Погрешность дискретизации поля градиента глубины в точке : .
Принимая во внимание следующие равенства:
, 
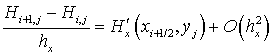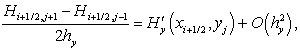
получим погрешность аппроксимации поля градиента глубины:
.
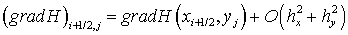Аналогичным образом можно получить аппроксимацию поля градиента глубины в точке :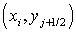 
.
Из выражения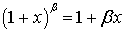 
, при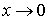 
следует равенство порядков погрешности аппроксимации полей 
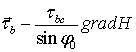и коэффициентов 
.
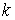В итоге получаем второй порядок погрешности аппроксимации по пространственным координатам для поля коэффициентов .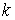
Таким образом, общий порядок погрешности аппроксимации математической модели транспорта наносов равен 
.
Литература:
1. Леонтьев И. О. Прибрежная динамика: волны, течения, потоки наносов. М.: Геос., 2001. 272с.
2. Сухинов А. И. Прецизионные модели гидродинамики и опыт применения в предсказании и реконструкции чрезвычайных ситуаций в Азовском море//Известия ТРТУ. — 2006. № 3 (58). С. 228–235.
3. Якушев Е. В., Сухинов А. И. Комплексные океанологические исследования Азовского моря в 28-м рейсе научно-исследовательского судна «Акванавт» // Океанология, 2003, т. 43, № 1, с.44–53.
4. Сухинов А. И., Чистяков А. Е., Проценко Е. А. Математическое моделирование транспорта наносов в прибрежной зоне мелководных водоемов// Матем. моделирование. 2013. Т. 25.№ 12. С.65–82.
5. Сухинов А. И., Никитина А. В., Чистяков А. Е., Семенов И. С. Математическое моделирование условий формирования заморов в мелководных водоемах на многопроцессорной вычислительной системе//Вычислительные методы и программирование. -2013. -Т. 14. С. 103–112.
6. Проценко Е. А., Чистяков А. Е., Программная реализация математической модели распространения поверхностных волн // Альманах современной науки и образования. -2013. -№ 1 (65). С. 170–173.
7. Проценко Е. А. Модель и алгоритмы решения задачи о транспорте наносов // Известия Южного федерального университета. Технические науки. 2009. Т. 97. № 8. С. 71–75.
8. Проценко Е. А. Двумерная конечно-разностная модель формирования наносов в прибрежной зоне водоема и ее программная реализация// Инженерный вестник Дона. 2010. Т. 13. № 3. С. 23–31.
9. Проценко Е. А. Программная реализация математической модели транспорта наносов в прибрежной зоне водоема// Вестник Таганрогского государственного педагогического института. 2012. № 1. С. 48–55.
10. Самарский А. А. Теория разностных схем. М. Наука, 1989.
11. Сухинов А. И. Двумерные схемы расщепления и некоторые их приложения. -М.: МАКС Пресс, 2005. -408 с.
12. Сухинов А. И., Чистяков А. Е., Фоменко Н. А. Методика построения разностных схем для задачи диффузии-конвекции-реакции, учитывающих степень заполненности контрольных ячеек // Известия Южного федерального университета. Технические науки. 2013. № 4. С. 87–98.
13. Сухинов А. И., Чистяков А. Е., Бондаренко Ю. С. Оценка погрешности решения уравнения диффузии на основе схем с весами//Известия ЮФУ. Технические науки. -2011. -№ 8 (121). С. 6–13.
