Турбулентное горение неперемешанных горючих газов, истекающих из прямоугольного сопла, находит широкое применение в самых различных областях техники — от обычных огнетехнических устройств ряда процессов химической технологии. В этом случае изучение их аэротермодинамических характеристик, с учетом кинетики процесса, представляет большой интерес. В тоже время детальное исследование горения неперемешанных газов, истекающих, из произвольного прямоугольного сопла практически отсутствует.
В рамках метода эквивалентной задачи теории теплопроводности расчет турбулентного диффузионного факела, истекающего из сопла прямоугольной формы, может дать удовлетворительные результаты, по-видимому, лишь в дальней области струи, где движение близко к осесимметричному [1].
[1].
В данной работе исследовано влияние соотношения сторон прямоугольного сопла (L) [3] и соотношение между исходными значениями скорости струи и спутного потока m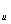 , а также влияние начальных значений тангенциальной скорости w на параметры факела.
, а также влияние начальных значений тангенциальной скорости w на параметры факела.
Существенной особенностью спутного струйного движения является его неавтомодельность, поэтому исследование таких течений может быть проведено путем численного решения более полной исходной системы уравнений на основе приближенных методов расчета. Рассмотрим реагирующую струю, вытекающую из сопла прямоугольной формы размером 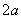 и
и 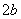 и распространяющуюся в спутном (затопленном) потоке воздуха. В качестве начала координат декартовой системы выберем центр начального сечения струи: ось
и распространяющуюся в спутном (затопленном) потоке воздуха. В качестве начала координат декартовой системы выберем центр начального сечения струи: ось 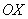 , направленной вдоль струи, а оси
, направленной вдоль струи, а оси 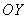 и
и 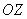 параллельны сторонам сопла. Предположим, что течение симметрично относительно оси
параллельны сторонам сопла. Предположим, что течение симметрично относительно оси 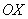 и плоскостей
и плоскостей 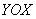 ,
, 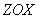 , которые образуют границу области интегрирования и которые позволяют рассматривать только одну четверть прямоугольной струи. В качестве горючего газа рассматривалась пропана- бутановая смесь, разбавленная инертным газом, а окислителем является воздух [3].
, которые образуют границу области интегрирования и которые позволяют рассматривать только одну четверть прямоугольной струи. В качестве горючего газа рассматривалась пропана- бутановая смесь, разбавленная инертным газом, а окислителем является воздух [3].
Параметры горючей струи и окислителя на срезе сопла задавались однородными и ступенчатыми значениями, а давления между собой равны.
Система дифференциальных уравнений, описывающая рассматриваемый процесс и граничные условия, метод решения аналогичны тем, которые приведены в работах [3÷4].
Рассматривалось диффузионное горение смеси пропана — бутана в воздухе со следующими исходными данными:
I. Зона окислителя: II. Зона горючего:
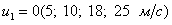 ;
; 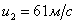 ;
;
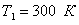 ;
; 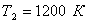 ;
;
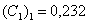 ;
; 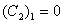 ;
; 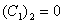 ;
; 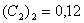 ;
;
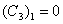 ;
; 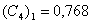 ;
; 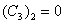 ;
; 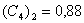 ;
;
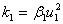
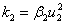
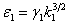
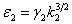
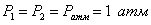 ;
; 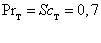 :
:
Кроме того, набор эмпирических констант, входящих в «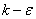 » модели турбулентности брались такими, как в работе [5].
» модели турбулентности брались такими, как в работе [5].
Некоторые численные результаты, касающиеся исследований влияния соотношения сторон прямоугольного сопла и спутности струи, т. е. параметра m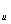 , а также входных условий на параметры диффузионного горения, приведены в виде графиков на рисунках 1÷3.
, а также входных условий на параметры диффузионного горения, приведены в виде графиков на рисунках 1÷3.
Выявлены, что для сопла (a:b)=(1:2) конфигурации трехмерного турбулентного диффузионного факела при различных значениях режимного параметра m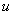 , 0
, 0 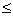 m
m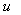
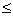 0,41, что при 0
0,41, что при 0 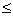 m
m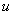
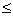 0,164 длина факела увеличивается, а дальше, с увеличением m
0,164 длина факела увеличивается, а дальше, с увеличением m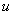 (m
(m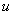
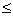 0,41) происходит укорачивание длины факела, что подтверждается экспериментальными материалами работы [1]. Увеличение параметра спутности m
0,41) происходит укорачивание длины факела, что подтверждается экспериментальными материалами работы [1]. Увеличение параметра спутности m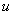 от нуля до 0,082 приводит к увеличению длины факела на один калибр от в выходного сечения сопла.
от нуля до 0,082 приводит к увеличению длины факела на один калибр от в выходного сечения сопла.
Обзор существующих литературных источников, особенно экспериментальных материалов, также подтверждает полученные нами результаты.
При распространении струи в затопленном потоке ширина зоны смещения наибольшая, а при увеличении спутности ширина зоны смещения становится уже, что приводит к быстрому затуханию продольной скорости (рис. 1). На рис. 2 в различных режимных параметрах m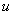 , приведены изменения кинетический энергии турбулентности в разных сечениях струи, соответственно по осям
, приведены изменения кинетический энергии турбулентности в разных сечениях струи, соответственно по осям 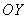 (сплошная линия) и
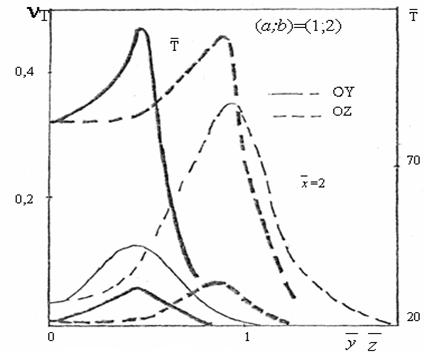
(сплошная линия) и 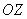 (пунктирная линия, mu=0,082), а жирные сплошная и пунктирная соответствуют при mu=0,41. На рис.3 в двух режимных параметрах mu, приведены изменения коэффициента кинематической турбулентной вязкости и температуры в разных сечениях струи по осям
(пунктирная линия, mu=0,082), а жирные сплошная и пунктирная соответствуют при mu=0,41. На рис.3 в двух режимных параметрах mu, приведены изменения коэффициента кинематической турбулентной вязкости и температуры в разных сечениях струи по осям 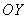 (сплошная линия) и
(сплошная линия) и 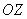 (пунктирная линия при mu=0,082), а жирные сплошные и пунктирные относятся к mu=0,41.
(пунктирная линия при mu=0,082), а жирные сплошные и пунктирные относятся к mu=0,41.
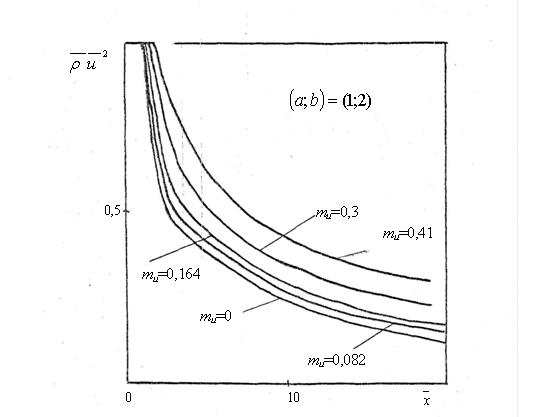
Рис. 1. Изменение плотности потока импульса вдоль оси факела при отношении сторон сопла (1; 2)
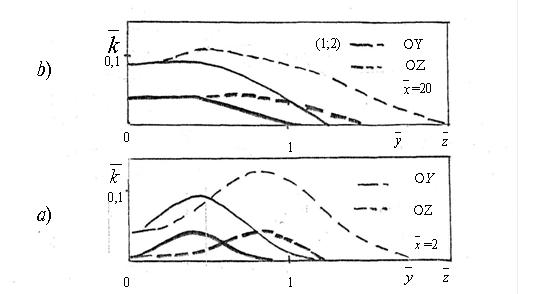
Рис. 2. Изменение кинетической энергии турбулентности в разных сечениях струи при 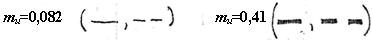
а)
б)
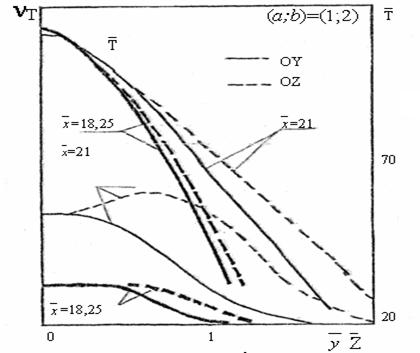
Рис. 3. Профили безразмерных температур и кинематической турбулентной вязкости в разных сечений струи при 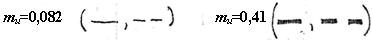
Эти результаты показывают, что максимальному значению кинетической энергии турбулентности и температуры соответствует максимальное значение кинематической вязкости, кроме этого, эти максимумы, с удалением от устья сопла смещаются к оси пламени. Из приведенных поперечных распределений кинематического коэффициента турбулентной вязкости и кинетической энергии турбулентности, при спутности mu=0,082, максимальное значение 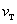 больше и шире смещения по сравнению с mu=0,41. Это можно объяснить тем, что увеличение спутности потока сжимает струю основного потока и тем самым уменьшает максимальное значения этих параметров, способствуя удлинению дальнобойности струи. Кроме того, можно отметить, что при малых значениях параметра спутности (mu=0; mu=0,082) ширина зоны смешения температуры шире, чем при mu=0,41 и спутность на максимальную температуру факела существенно не влияет.
больше и шире смещения по сравнению с mu=0,41. Это можно объяснить тем, что увеличение спутности потока сжимает струю основного потока и тем самым уменьшает максимальное значения этих параметров, способствуя удлинению дальнобойности струи. Кроме того, можно отметить, что при малых значениях параметра спутности (mu=0; mu=0,082) ширина зоны смешения температуры шире, чем при mu=0,41 и спутность на максимальную температуру факела существенно не влияет.
Численно получено, что в случае соотношения сторон сопла (а: в)=(1:4), заданная тангенциальная скорость на устье сопла 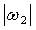 х=0=6,1
х=0=6,1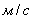
 приводит к уменьшению длины факела на 11 %, в сравнении с ее значением, равным нулю.
приводит к уменьшению длины факела на 11 %, в сравнении с ее значением, равным нулю.
Можно отметить, что при соотношении сторон (1:4) длина факела укорачивается примерно в три раза, в сравнении с соотношением сторон (1:1). Это может быть объяснено тем, что увеличение соотношения сторон сопла приводит к сильному влиянию градиента скорости, направленного вдоль потока на линейный масштаб турбулентности. Расчеты приведены до смыкания максимальной температуры по оси y и z на оси струи x.
Необходимо отметить, что влияние входного значения тангенциальной скорости на максимальное значение температуры существенно не влияет.
Литература:
1. Вулис Л. А., Ярин Л. П. Аэродинамика факела. — Л.: Энергия. 1978., -216с.
2. Мак-Гирк Дж.Дж., РОДИ В. Расчет трехмерных турбулентных свободных струй.//В сб. Турбулентные сдвиговые течения.Т.1.М.:Машиностроение, 1982, с.72–88.
3. Ходжиев С., Жумаев З. Ш., Пиримов А., Муминова З. А. Исследование трехмерных турбулентных струй реагирующего газа, истекающего из прямоугольного сопла и распространяющегося в спутном (затопленном) потоке воздуха при диффузионном горении. // Узбекский журнал Проблемы механики -1993., № 2., с.28–33.
4. Ходжиев С., Авезов А. Х., Муродов Ш. Н. Численное моделирование трехмерных турбулентных струй реагирующих газов, истекающих из сопла прямоугольной формы, на основе алгебраической модели турбулентности. // Узбекский журнал Проблемы информатики и энергетики -2007., № 3.
5. Ходжиев С., Авезов А. Х., Муродов Ш. Н. Численное моделирование трехмерных турбулентных струй реагирующих газов, истекающих из сопла прямоугольной формы, на основе «К-ε» модели турбулентности.//Научный вестник Бухарского государственного университета -2007., № 3., с.81–87.







