На кафедре «Начертательной геометрии и инженерной графики» Ташкентского института ирригации и мелиорации студентам первого курса бакалавриатуры проводится занятие по разделу «Проекции геометрических тел», где выдаются различные геометрические фигуры. На занятиях объясняется и показывается задание для выполнения графических работ по вычерчиванию геометрических фигур: призмы, пирамиды и т. д. по техническим деталям контурных их состоят из линий разного вида линий: прямых, дуг, окружностей и т. д. Поэтому для выполнения чертежей требуется знание геометрических построений — деление отрезка прямой, деление окружностей и т. п. На занятиях приводится пример деления окружностей на равные части и каждому студенту для самостоятельной графической работы выдается вариант задания с указанием числовых величин диаметра окружности и числа сторон многоугольника.
Выдаются задания: начертить на горизонтальной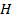 
плоскости окружность диаметром 
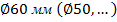и разделить их на три (четыре, …)
- построить на них треугольник (четырехугольник, пятиугольник, …) описанный и вписанный в данную окружность;
- выделить в горизонтальной 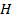плоскости вписанный в окружности треугольник, как пирамиду, а описанный в окружности треугольник как призму;
- спроектировать на недостающих проекциях фронтальной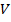 
и профильной 
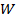плоскостях пирамиду и призму с высотой 
.
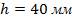По литературным источникам [1, 2] известны методы деления окружности на равные части и построения их, как вписанных в окружность многоугольников. Разделение окружности на равные части можно несколькими способами: при помощи графических (рисунок 1, а, б) построений, с помощью таблицы хорд (таблица 1), с помощью циркуля (рисунок 2, а, б и в), с помощью транспортера и угольных линеек.
Таблица 1
Численные значения длины отрезка хорд
|
n |
3 |
34 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
14 |
15 |
16 |
|
K |
0,866 |
0,707 |
0,587 |
0,5 |
0,434 |
0,383 |
0,342 |
0,309 |
0,259 |
0,223 |
0,208 |
0,195 |
|
Примечание: n — число делений окружности; K — коэффициент уменьшения диаметра. |
||||||||||||
а) б)
Рис. 1. Графический способ построения многоугольника.
Нами приводится методика построения описанной в окружности многоугольника, например, треугольника. Чертим осевые — горизонтальные и вертикальные линии и вычерчиваем окружность, например, диаметром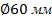 
(рисунок 2, а). При помощи циркуля, радиусом 
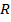окружности, делим данную окружность на равные части и вершины треугольника фиксируем точками 
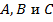. Соединяя эти точки, получим вписанный треугольник 
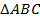. Для получения описанного по окружности 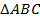, мы находим и определяем максимальное расстояние отрезка по сектору 
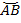. Можно определить двумя способами: 1 — по вертикальной осевой линии от центра 
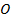окружности на пересечения сторон отрезка 
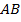и окружности фиксируем две точки: 
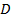и 
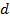; 2 — радиусом 
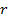, от точек 
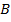и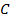 
проводим засечки в двух местах и соединяя их делим отрезок 
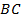пополам, место соединения этих линий будет 
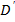и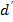 
. Расстояние отрезка двух точек 
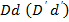является максимальное расстояние отрезка по сектору 
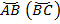и фиксируем этот расстояние как радиус малой окружности, т. е.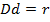 
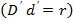, в отличие от большой 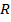окружности.
По вершинам остроконечности треугольника 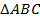вычерчиваем дуги малой окружности радиусом 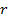(рисунок 2, б). Например, по вершинам двух дуг (точка а и точка в) проводим касательную (сопряженную) линию, тогда данная линия получается как параллельная линия 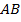, т. е. отрезки 
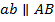. То же самое происходит и с другими линиями: от точек «
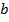» и «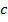
» проводим касательную линию, которая является параллельной линией — 
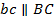. Аналогично происходит и с вершинами хорд «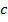» и «
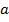» — получаем 
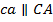. После полученных трех вспомогательных отрезков 
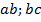; и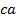 
, которые расположены вне окружности и эти вспомогательные линии доводим их до пересечения между ними (рисунок 2, в). Место пересечения их обозначим буквами
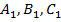и после обведения контурными линиями — получим описанный по окружности 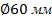треугольник 
.
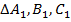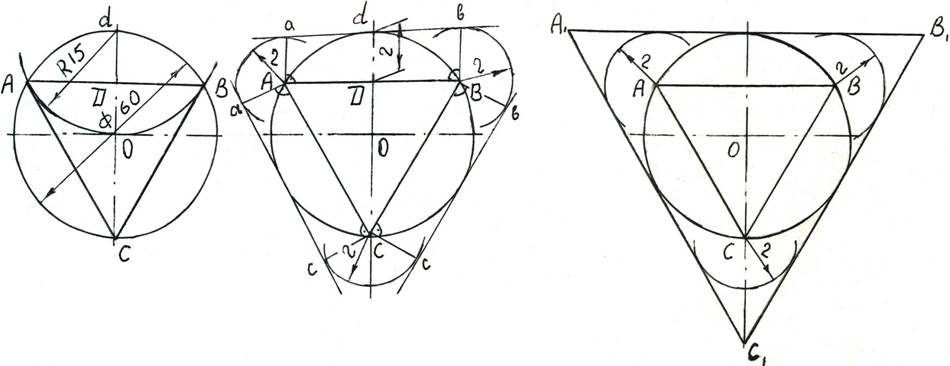
а) б) в)
Рис. 2. Метод построения вписанной и описанной по окружности треугольника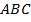 
, где: а) — деление окружности на три части — 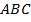; б) — построение вписанной в окружности треугольника 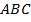; в) — построение описанной по окружности треугольника .
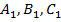На рисунке 3 приводится построения на горизонтальной 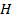проекции описанный и вписанный в окружность треугольник. При помощи циркуля, радиусом 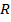окружности, делим данную окружность на равные части и вершины треугольника фиксируем точками 
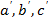. Соединяя эти точки, получим вписанный треугольник 
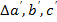. Также по деленным точкам описанного в окружности получаем другой треугольник 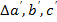. В дальнейшем из горизонтальной проекции проводим во фронтальную 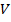проекцию ортогональные линии и фиксируем нижнюю часть основания призмы 
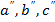. Строим по выданным параметрам 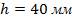высоту призму и на этой полученной высоте призмы определяем ортогональную проекцию основания пирамиды 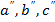. После этого, также по данной высоте 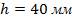строим пирамиду с вершиной 
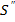. Полученная фигура состоит из двух геометрических тел — призмы 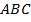и пирамиды 
.
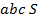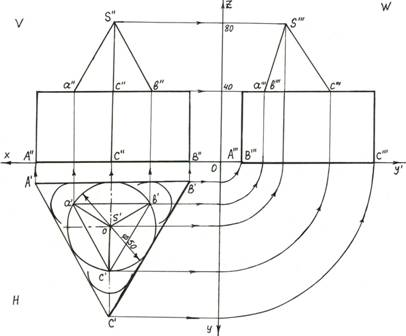
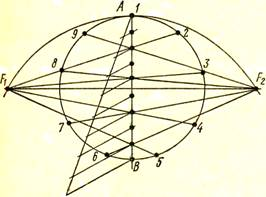
Рис. 3. Пример построения двух геометрических фигур на одной модели: призмы 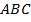и пирамиды .
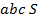Далее по ортогональным проекциям строим данную фигуру в профильной 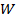проекции. Студент по своему выбору может спроектировать другой модель, т. е. вписанный треугольник выбрать как пирамиду 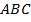, а описанный по окружности треугольник — призму 
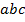(рисунок 4). Аналогичные построения этого примера будет как и в предыдущем построении данной модели.
Здесь в отличие от предыдущего примера, описанная по окружности треугольник 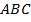является основанием усеченной, по горизонтали, пирамиды, а вписанный треугольник 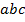— призмой. Нижняя часть модели является усеченная трехгранная пирамида, а верхняя часть — трехгранная призма.
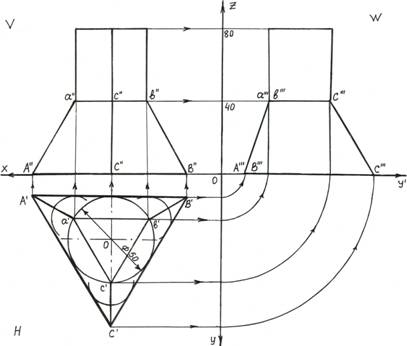
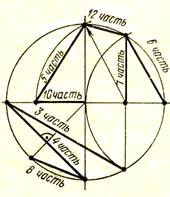
Рис. 4. Построение двух геометрических фигур на одной модели: усеченной пирамиды 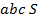и призмы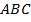
Каждому студенту для самостоятельной графической работы выдается вариант задания с указанием численных величин диаметра окружности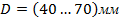 
, число сторон многогранников 
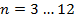и, варьируя двумя величинам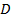и и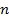 
получим более тридцати вариантов. Также по такому же методу можно проделать и с четырехугольником, пятиугольником и т. д. — находим вписанный четырехугольник (пятиугольным) потом уже описанный по окружности четырехугольник.
Из выше приведенного можно сделать следующие выводы:
- при построении многоугольника надо разделить окружность на равные части (3) и построить в начале вписанный многоугольник, также следом за ним описанный по окружности многоугольник;
- при построении геометрической фигуры модели необходимо начать строить с горизонтальной 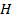проекции, затем фронтальную 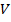и профильную ;
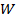- студент может самостоятельно спроектировать по своему выбору на одной модели две разные геометрические фигуры: призму и пирамиду;
- при построении на горизонтальной проекции из двух многоугольников необходимо сначала выбрать пирамиду, а затем уже призму.
Литература:
1. Брилинг Н. С., Евсеев Ю. П. Задания по черчению: — 2 изд, М.: Строй издат, 1984. 256 с.
2. Миронова Р. С., Миронов Б. Г. Сборник заданий по черчению. М.: Высш. шк., 1984.264с.
