В данной работе рассматривается задача об установлении формы и фазовой скорости длинных волн, которые могут существовать на течении. Показано, что в случае конечной глубины жидкости скорость горизонтального течения должна меняться с глубиной по линейному закону. В линейной постановке определены профиль и фазовая скорость волны.
Ключевые слова: длинные волны, течение, профиль волны, фазовая скорость.
При изучении гашения волн течением необходимым этапом, представляющим и самостоятельный интерес, является установление формы волн, которые могут существовать на течении. Проследим последовательно все аспекты этой задачи.
1. Общая постановка задачи.
Рассматривается плоское движение идеальной несжимаемой однородной тяжелой жидкости относительно неподвижных осей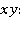 
ось 
направлена горизонтально, ось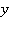 
— вертикально вверх. Такое движение описывается с помощью следующей системы уравнений [1]:
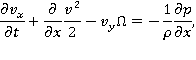
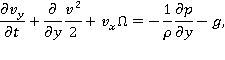
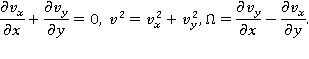
Здесь обозначено: 
— время;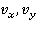 
— компоненты скорости; 
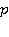— давление; 
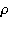— плотность; 
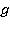— ускорение свободного падения; 
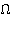— вихрь скорости, направленный перпендикулярно плоскости течения. Будем считать, что жидкость снизу ограничена горизонтальным непроницаемым твердым дном 
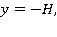а сверху — свободной поверхностью. При этом ось направлена вдоль невозмущенного уровня свободной поверхности.
2. Вывод интеграла Бернулли.
Рассмотрим горизонтальное движение жидкости — течение. При этом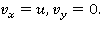 
Исходная система уравнений примет вид:
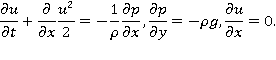
Отсюда получаем, что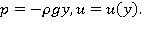 
Будем считать, что течение, для которого
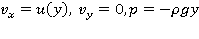
сопровождается некоторым волновым движением. Это волновое движение будем считать потенциальным. Тогда поле скоростей можно представить в виде:
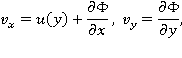
где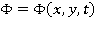 
— потенциал скорости волнового движения жидкости.
Далее будем рассматривать волны установившегося вида, когда функция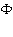 
зависит от 
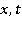посредством комбинации 
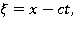где 
— искомая фазовая скорость волны. Введем также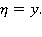 
При этом
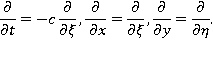
В результате указанных подстановок исходную систему уравнений можно представить в виде:
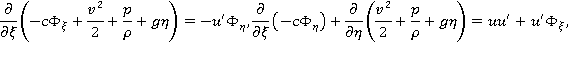
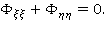
Продифференцируем первое из уравнений по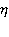 
, а второе уравнение — по 
:
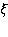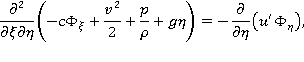
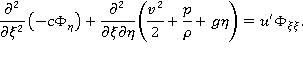
Вычитая из второго уравнения первое, получим:
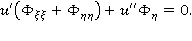
Так как 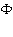является гармонической функцией, то имеем 
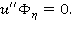Исключая случай 
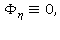получим 
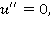откуда имеем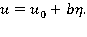 
Таким образом, для сосуществования потенциального движения жидкости и течения, изменяющегося с глубиной, необходимо, чтобы скорость течения линейно изменялась с глубиной погружения. При этом вихрь скорости совместного движения жидкости (течение и волны) будет постоянен для всей массы жидкости. Величина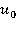 
есть скорость потока при 
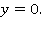Пусть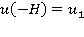 
.Тогда 
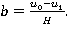Отсюда следует, что, если 
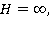то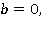 
вихрь отсутствует, и вся масса жидкости будет двигаться с постоянной скоростью 
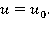При конечной глубине жидкости можно считать, что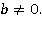 
Умножая первое уравнение на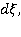 
а второе уравнение на 
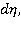получим:
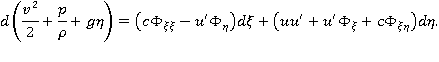
Заметим, что
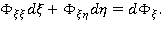
Тогда
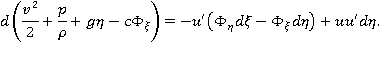
Теперь рассмотрим уравнение для линий тока. Если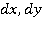 
есть компоненты элементарного смещения вдоль линии тока, то ее уравнение записывается в виде:
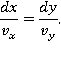
Так как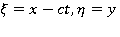 
то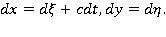 
Поэтому получаем
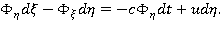
Теперь можно написать, что
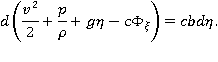
Отсюда заключаем, что вдоль линии тока может иметь место следующий интеграл:
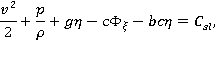
где постоянная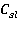 
зависит от линии тока. Запишем этот интеграл в виде:
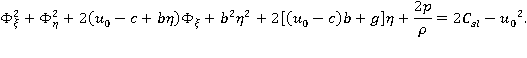
Таким образом, потенциал скорости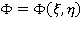 
удовлетворяет уравнению Лапласа, а давление можно определить из предыдущего уравнения.
3. Краевые условия.
На свободной поверхности выполняются кинематическое и динамическое условия. Пусть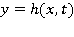 
есть уравнение свободной поверхности, тогда имеем:
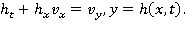
В переменных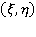 
кинематическое условие принимает вид:
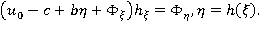
Динамическое условие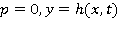 
в переменных принимает вид:
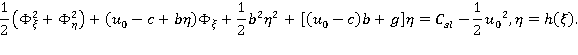
Условие непротекания жидкости через дно, условие периодичности движения и тот факт, что средний уровень свободной волновой поверхности совпадает с осью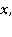 
соответственно, имеют вид:
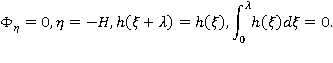
4. Линейная задача о волнах на течении.
Кинематическое и динамическое условия принимают в этом случае вид:
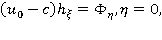
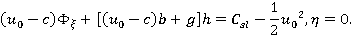
Отыскивая решение уравнения Лапласа методом разделения переменных Фурье [2] и удовлетворяя условию непротекания на дне, получим:
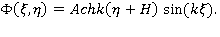
Из кинематического условия имеем:
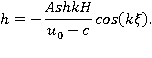
Уравнение для определения фазовой скорости получается из динамического условия:
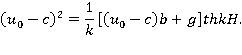
Таким образом мы определили, в случае линейной задачи, форму и фазовую скорость периодических волн, которые могут существовать на горизонтальном течении с линейно изменяющейся по глубине скоростью в жидкости конечной глубины.
Литература:
1. Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика. Ч.1. — М.: Физматгиз, 1963.
2. Сретенский Л. Н. Теория волновых движений жидкости. — М.: Наука, 1977.
