В последние годы проблеме управления упругими манипуляторами уделяется особое внимание. Вначале, проводимые исследования концентрировались на одном упругом звене. В большинстве предлагаемых прежде стратегий управления, упругим звеном использовалась модель пространства состояний [1, 2, 3], в некоторых других — передаточная функция системы.
Упругое дифференциальное звено описывается следующим дифференциальным уравнением
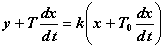 , где y, x — координаты, T, T0 — время, k — коэффициент усиления.
, где y, x — координаты, T, T0 — время, k — коэффициент усиления.
Передаточная функция звена
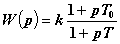
Существенным параметром звена является коэффициент 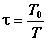 . Если
. Если 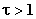 , то звено ближе к реальному дифференцирующему звену
, то звено ближе к реальному дифференцирующему звену 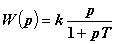 .
.
Упругое интегрирующее звено описывается следующим дифференциальным уравнением
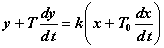
Передаточная функция звена
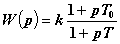
Существенным параметром звена является коэффициент 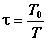 , причём
, причём 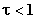
В [4–6] предполагается, что передаточная функция использует вращающий момент упругого звена как вход, а смещение концевой точки звена — как выход. Эти модели получены путем использования метода, который представляет упругое нормальное отклонение иу(x, t)как
иу(x, t)=∑qi(t)*Ψi(x), (1)
где qi — обобщенные координаты;
Ψi(x) — собственная функция, зависящая от длины балки.
Учитывая отсутствие демпфирования, это выражение можно представить в виде рациональной передаточной функции
Y(s) /u(s) = (an s2n + an-1s 2n-2+an-2s2n-4+…+ a0)/s2(s2n+bn-1s2n-2+bn-2s2n-2+…b0)(2)
где u(s) — входной момент,
y(s) — выход, полое перемещение концевой точки звена.
Проблема возникает, когда значение степени n в (2) повышается, что делается для повышения точности модели. В [7] показано, что при возрастании п, коэффициент аnпередаточной функции в (2) стремится к нулю и одновременно следующий коэффициент ап-1стремится к бесконечности. Из этого следует, что в пределе относительная степень передаточной функции не определена. Если относительная степень функции передачи выражена неотчетливо, то реализовать этот метод в системе управления сложно. Кроме того, любая попытка идентификации вида передаточной функции будет затруднена. Чтобы решить эту проблему, нами предлагается альтернативная выходная переменная, которая определяется как разница в отклонениях жесткого и упругого звеньев. С использованием альтернативной переменной смещение концевой точки определено как
Yref = l*θh(t) — uy(l, t)
Эта переменная физически измеряемая. Создание стабилизирующего регулятора, использующего Y или Yrefвкачестве выходного параметра системы, дает возможность достижения установившегося состояния выхода. В обоих случаях величина установившегося состояния выхода равна l*θss, где θss-установившаяся величина выхода θh(t). Стабилизирующий регулятор демпфирует колебания: uy(l, t) →0, при t →∞.
Осуществить управление упругими манипуляторами для достижения и сохранения точного местоположения довольно сложно. Не случайно, что решению этой задачи посвящено множество исследований. Отклонение концевой точки упругого звена является важным параметром управления, помогающим добиться непрерывного отслеживания траектории. В некоторых случаях для вычисления крутящего момента в частотной области нормальное упругое отклонение концевой точки звена принимается равным нулю. Для измерения упругого отклонения вибрирующего звена Джнифене и др. применяли тензодатчики. Отклонение использовали как ошибку ввода (погрешность по входу) в системе управления с нечеткой логикой с целью уменьшения вибрации схвата манипулятора в ответ на ступенчатое входное воздействие.
В данной работе предлагается использовать ошибку положения концевой точки звена (схвата) в обратной связи на входе ПД-регулятора. Полное перемещение yrefможно представить как функцию движения жёсткого манипулятора l*(θh(t)-θ(l)) и нормального упругого отклонения uy(l, t), ввиде:
yref = l * (θh(t)-θ(l)) — uy(l, t)
где θ(l) — угол поворота поперечного сечения концевой точки предыдущего упругого звена. Он равен нулю для первого звена, потому что его привод зафиксирован на жестком основании.
В работе предлагается структура системы управления, в которой используется пропорционально-дифференциальный регулятор, а адаптивная нейронная сеть (НС) обучается в режиме реального времени управлять упругим отклонением и компенсировать нелинейности системы.
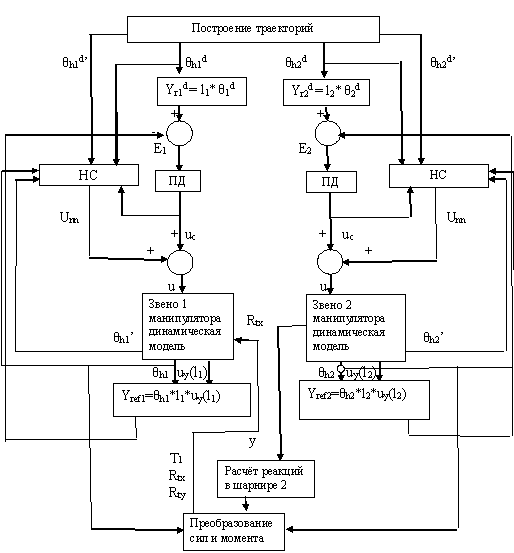
Рис. 1. Структурная схема системы управления
На схеме: НС — нейросеть; ПД — регулятор; θh1,θh2 — перемещение звеньев 1 и 2 соответственно; θh1’,θh2’ — скорости1 и 2 соответственно; E1, E2 — ограничения для условий критериев роста НС; Unn — выходные значения нейросети; l1 l2 — длины звеньев 1 и 2 соответсвенно; u — сигнал управления; uc — выходные значения типового регулятора; θh1d,θh2d,θh1d’,θh2d’- заданные значения перемещения и скорости первого и второго звена сооответственно; Yref1,Yref1 — предложенные нами преобразованные выходные параметры системы(смещение концевой точки звена 1 и 2 соответсвенно); Rtx, Rty — преобразованные моменты сил для первого звена по осям x и y соответственно; T1 — сила реакции звена;
Эта структура управления реализуется методом рекурсивной процедуры для моделирования многозвенного упругого манипулятора с целью гашения вибраций и компенсации отклонения концевой точки упругого звена. Требуемое полное отклонение концевой точки определяется как
Ytd= l*θhd(t)
Такой подход позволяет осуществлять управление перемещением манипулятора с заданной точностью и допустимой амплитудой колебаний в режиме реального времени
Литература:
1. Cannon R. H., Schmitz E. Initial experiment on the end-point control of a flexible one-link robot// Int. J. Robot. Res. -1984.-Vol. 3, № 3.-P.62–75.
2. Hastings G., Book W. J. Experiments in the optimal Control of a Flexible Manipulator // Proceedings ACC, Summer, 1985.
3. Hastings G. G., Book W. J. Verification of a Linear Dynamic Model for Flexible Robotic Manipulators // Proceedings of IEEE Int. Conf. on Robotics and Automation. — 1986. -P. 1024–1029.
4. Wang D., Vidyasagar M. Modelling and Control of a Flexible Beam Using the Stable Factorization Approach // Winter Annual Meeting of the ASME, Winter, 1986.
5. Wang D., Vidyasagar M. Modelling of a 5-Bar-Linkage Manipulator with One Flexible Link // Winter Annual Meeting of the ASME, 1988.
6. Krishnan H. Bounded Input Discrete-Time Control of a Single-Link Flexible Beam // Master's Thesis. — University of Waterloo, Ont, 1988.
7. Wang D., Vidyasagar M. Transfer Function for a Single Flexible Link // IEEE Int. Conf. on Rob. and Auto. — Scottsdale, AZ, 1989-P. 1042–1047.
8. Piedboeuf J-.C, Hurteau R. Modelling and analysis of a two degree of-freedom robot with a flexible forearm // Canadian J. of Elec. and Computer Eng.-1991.-Vol. 16,№ 4.-P.127–134.
9. Tzes А. Р., Yurkovich S., Langer F. D. A method for solution of the Euler-Bernoulli beam equation in flexible-link robotic systems // Proc. IEEE Int. Conf. on Robotics and Automation. — Scottsdale: AZ, 1989.-P. 557–560.
10. Bayo E. Computed Torque for the Position Control of Open-Chain Flexible Robots // IEEE International Conference on Robotics and Automation. — 1988.-Vol. 1.-P. 316–321.
11. Alhaj M. Technologies for Autonomous Navigation in Unstructured Outdoor Environments // Ph.D. Thesis / University of Cincinnati (2003).
12. Аль-Кхаиит Саад Загхлюл Сайд. Метод управления роботом-манипулятором с упругими звеньями // 58-я научная конференция / ЮР-ГТУ (НПИ), г. Новочеркасск, 6 апреля — 11 мая 2009 г. — Новочеркасск, 2009.-С 31-







