Разработанные лауреатом Нобелевской премии Л. В. Канторовичем методы линейного программирования до сих пор не потеряли свою актуальность, в том числе целочисленные модели [1…6]. Последние широко используются и в строительном производстве, прежде всего в задачах оптимального раскроя материалов и использования оборудования.
1.Задача оптимального раскроя материалов. На предприятии производится раскрой m различных партий материалов соответственно в количестве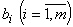
единиц одинакового размера в каждой партии. Из материалов всех партий требуется изготовить максимальное число комплектов Z, в каждый из которых входит p различных видов деталей соответственно в количестве 
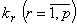единиц, если известно, что каждую единицу материала можно раскроить на детали n различными способами, причем при раскрое единицы 
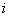-й партии j-м способом получается 
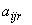деталей r-го вида.
Для составления математической модели задачи обозначим через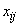 
число единиц материала i-й партии, которые будут раскроены j-м способом. Тогда из i-й партии при j-м способе раскроя получим 
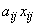деталейr-го вида. Из всей же i-й партии при применении к ней всех n способов раскроя получим деталей r- го вида 
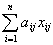, а из всех m партий их будет получено 
.
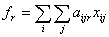В каждый комплект должно входить 
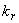деталей, поэтому отношения 
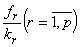определяют количество комплектов, которые можно составить из деталей r-го вида. Количество полных комплектов по всем видам деталей определится наименьшим из этих отношений, и оно должно быть целым.
В случае полной комплектности выполняется равенство отношений: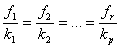 
, откуда 
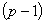отношений можно выразить через любое из них, например, через 
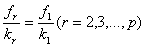или через 
.
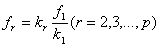Заменяя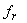 
и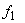
их значениями, получим 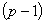ограничений по комплектности:
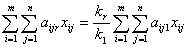
или
.
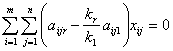
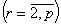Учитывая имеющееся количество единиц материала в партиях, получим m ограничений по ресурсам:
.
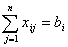
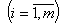Все 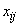удовлетворяют условию неотрицательности:
.
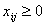
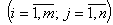Таким образом, требуется определить наибольшее значение функции
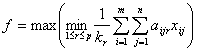
при ограничениях
,
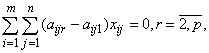
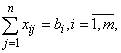
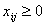
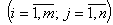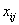- целые.
Рассмотрим практическую задачу, возникшую при разработке проекта домов из бруса.
Определить способы распила двух партий бревен для получения максимального числа комплектов, состоящих из двух брусьев длиной 2,2 м и одного длиной 1,3 м. Первая партия состоит из 99 бревен длиной 6,6 м, вторая — 60 бревен по 4,8 м.
Составимвозможные способы распила, определим значение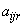 
, где i=1,2; r=1,2 (табл.1).
Таблица 1
Способы распила
|
Партия |
Размер брусьев |
j=1 |
j=2 |
j=3 |
j=4 |
f1 |
|
I (i=1) (6,6 м) |
2,2 м (r=1) 1,3 м (r=2) |
3 — |
2 1 |
1 3 |
— 5 |
f1 f2 |
|
II (i=2) (4,8 м) |
2,2 м (r=1) 1,3 м (r=2) |
2 — |
1 2 |
— 3 |
— — |
f1 f2 |
Обозначим через 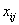(i=1,2; j=1,2,3,4) количество бревен в первой и второй партиях, распиленных 1,…,4 способами, и составим математическую модель задачи.
Выражение для целевой функции определим из условия комплектности. Имеем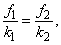 
то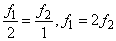 
; 
.
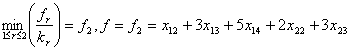Ограничение по комплектности получим из равенства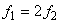 
:
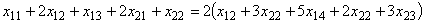
или
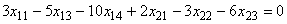
С учетом ограничений по материальным ресурсам, получим искомую математическую модель:
найти максимальное значение линейной функции
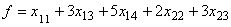
при ограничениях
,
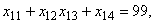
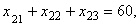
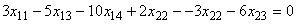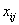- целые;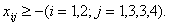 
Принимая за базисные переменные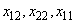 
, получим
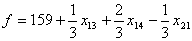
при ограничениях
.
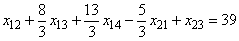
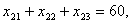
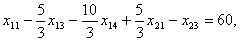
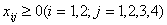Далее примем за базисные переменные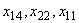 
. Получили искомый оптимальный план: 
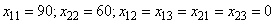(90 бревен по 6,6 м распилить на 3 части по 2,2 м; 9 бревен по 6,6 м — на 5 частей по 1,3 м; 60 бревен по 4,8 м — на 5 частей по 1,3 м; 60 бревен по 4,8 м — на 3 части (один имеет длину 2,2 м; а два других -1,3 м)). При этом максимальное количество комплектов
.
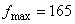2. Задача оптимального использования оборудования. На домостроительном комбинате имеется m видов оборудования соответственно в количестве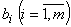
единиц. На каждом виде оборудования можно изготавливать n видов деталей, которые входят в комплект соответственно в количестве 
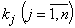единиц.
Пусть aij-производительность i-го вида оборудования при изготовлении j-го вида детали. Необходимо составить план использования оборудования, который обеспечит максимальный выпуск комплектной продукции. Обозначим через 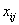количество i-го оборудования, на котором изготавливаются детали j-го вида. За единицу времени их будет произведено 
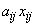единиц, а на всех видах оборудования -
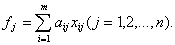
Так как в каждый комплект должно входить k деталей, то отношения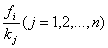 
определяют количество комплектов, которое можно составить из деталей j-го вида. Количество полных комплектов по всем видам деталей определяется наименьшим из этих отношений. Для соблюдения условия полной комплектности, очевидно, должно выполняться равенство отношений 
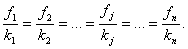Отсюда получим 
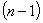ограничений по комплектности:
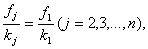
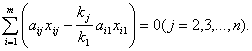
Так как предполагается, что оборудование используется полностью, то получим дополнительные m ограничений:
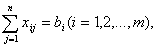
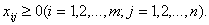
Таким образом, требуется найти наибольшее значение функции
при ограничениях
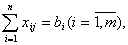
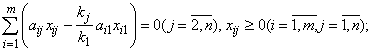
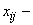целые.
Как видим, задача является частным случаем задачи оптимального раскроя материалов.
С математической точки зрения задачи целочисленного программирования нередко обладают повышенной сложностью. Даже в простых задачах введение дополнительных требований целочисленности неизвестных приводит к невозможности их решения обычными методами. Поэтому используются приближенные методы; методы отсечения (вводятся дополнительные ограничения, «отсекающие» нецелочисленный план); метод перебора (отбрасываются варианты, заведомо не являющиеся оптимальными).
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
2. Будылина Е. А.,Гарькина И. А., Данилов А. М. Декомпозиция динамических систем в приложениях / Региональная архитектура и строительство.– 2013. — № 3(17). — C. 95–100.
3. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
4. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях/ Молодой ученый. –2013. — № 5. — С. 42–45.
5. Гарькина И. А., Данилов А. М., Жегера К. В. Математическое программирование в управлении качеством материалов / Региональная архитектура и строительство. –2014. –№ 1. –С. 30–36.
6. Гарькина И. А., Данилов А. М., Пылайкин С. А. Из опыта математического моделирования при решении прикладных задач / Альманах современной науки и образования. –2014. –№ 2 (81). — С. 35–37.
