Значительная часть экономических задач, относящихся к линейному программированию, требует целочисленного решения [1…6]. К ним, например, относятся задачи, в которых переменные означают количество единиц продукции. Здесь требуется найти максимальное (минимальное) значение линейной функции
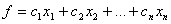
при ограничениях
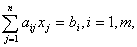
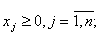
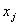 — целые.
— целые.
Рассмотримпрактическую задачу по установке на предприятии дополнительного оборудования, для размещения которого выделяется 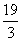 м2 площади. На приобретение оборудования предприятие может израсходовать 10 млн. руб., при этом оно может купить оборудование двух видов. Комплект оборудования 1 вида стоит 1000 руб., а 2 вида — 3000 руб. Приобретение одного комплекта оборудования 1 вида позволяет увеличить выпуск продукции в смену на 2 единицы, а одного комплекта оборудования 2 вида — на 4 единицы. Зная, что для установки одного комплекта 1 вида требуется 2 м2 площади, а оборудования 2 вида — 1 м2 площади, определить такой набор дополнительного оборудования, при котором выпуск продукции будет максимальным.
м2 площади. На приобретение оборудования предприятие может израсходовать 10 млн. руб., при этом оно может купить оборудование двух видов. Комплект оборудования 1 вида стоит 1000 руб., а 2 вида — 3000 руб. Приобретение одного комплекта оборудования 1 вида позволяет увеличить выпуск продукции в смену на 2 единицы, а одного комплекта оборудования 2 вида — на 4 единицы. Зная, что для установки одного комплекта 1 вида требуется 2 м2 площади, а оборудования 2 вида — 1 м2 площади, определить такой набор дополнительного оборудования, при котором выпуск продукции будет максимальным.
Составим математическую модель задачи. Предположим, что предприятие приобретает 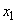 комплектов оборудования 1 вида и
комплектов оборудования 1 вида и 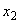 комплектов оборудования 2 вида. Тогда переменные
комплектов оборудования 2 вида. Тогда переменные 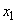 и
и 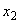 должны удовлетворять следующим неравенствам:
должны удовлетворять следующим неравенствам:
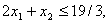
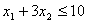 .
.
Если предприятие приобретет указанное количество оборудования, то общее увеличение продукции составит 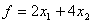 . По своему экономическому содержанию переменные
. По своему экономическому содержанию переменные 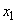 и
и 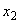 могут принимать лишь целые неотрицательные значения, то есть
могут принимать лишь целые неотрицательные значения, то есть 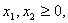
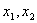 — целые. Многоугольник решений задачи, состоящей в определении максимального значения линейной функции f при выполнении заданных ограничений, приводится на рис.1.
— целые. Многоугольник решений задачи, состоящей в определении максимального значения линейной функции f при выполнении заданных ограничений, приводится на рис.1.
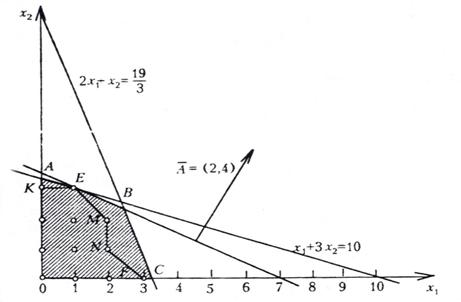
Рис. 1.
Координаты всех точек многоугольника решений ОАВС удовлетворяют системе заданных линейных неравенств и условию не отрицательности переменных. Вместе с тем, условию целочисленности переменных удовлетворяют координаты лишь 12 точек, отмеченных на рис. 1. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник ОАВС многоугольником OKEMNF, который содержит все допустимые точки с целочисленными координатами и координаты каждой из вершин являются целыми числами. Значит, координаты точки максимума функции f на многоугольнике OKEMNF определяют оптимальный план задачи.
Построим вектор 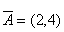 и прямую
и прямую 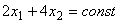 , проходящую через многоугольник решений OKEMNF. Прямую будем передвигать в направлении вектора
, проходящую через многоугольник решений OKEMNF. Прямую будем передвигать в направлении вектора 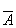 до тех пор, пока она не пройдет через последнюю общую точку ее с данным многоугольником. Координаты этой точки и определят оптимальный план с максимальным значением целевой функции. В данном случае искомой является точка Е(1,3), в которой целевая функция принимает максимальное значение
до тех пор, пока она не пройдет через последнюю общую точку ее с данным многоугольником. Координаты этой точки и определят оптимальный план с максимальным значением целевой функции. В данном случае искомой является точка Е(1,3), в которой целевая функция принимает максимальное значение  . В соответствии с этим планом, предприятию следует приобрести один комплект оборудования 1-го вида и три комплекта оборудования 2-го вида. Это обеспечит предприятию при имеющихся у него ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции на 14 ед. в смену.
. В соответствии с этим планом, предприятию следует приобрести один комплект оборудования 1-го вида и три комплекта оборудования 2-го вида. Это обеспечит предприятию при имеющихся у него ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции на 14 ед. в смену.
Существует ряд методов решения задачи целочисленного программирования. Наиболее распространенным из них является метод Гомори, при котором нахождение решения задачи целочисленного программирования начинают с определения симплексным методом оптимального плана задачи без учета целочисленности переменных. После того как план найден, просматривают его компоненты. Если среди компонентов нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования. Если же в оптимальном плане задачи переменная принимает дробное значение, то к системе уравнений добавляют неравенство
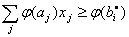 ,
,
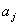 и
и 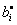 — соответствующие оптимальному плану значения
— соответствующие оптимальному плану значения 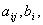 а
а 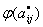 и
и 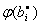 - дробные части чисел (под дробной частью числа
- дробные части чисел (под дробной частью числа 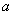 понимается наименьшее отрицательное числоq, такое, что разность между
понимается наименьшее отрицательное числоq, такое, что разность между 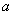 и q есть целое). И снова решают задачу линейного программирования. Если в оптимальном плане задачи без учета целочисленности дробные значения принимают несколько переменных значений, то дополнительное неравенство определяется наибольшей дробной частью. Если в найденном с учетом добавленного неравенства плане задачи переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования, либо устанавливают ее неразрешимость.
и q есть целое). И снова решают задачу линейного программирования. Если в оптимальном плане задачи без учета целочисленности дробные значения принимают несколько переменных значений, то дополнительное неравенство определяется наибольшей дробной частью. Если в найденном с учетом добавленного неравенства плане задачи переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования, либо устанавливают ее неразрешимость.
Проиллюстрируем приведенный метод на конкретном примере: определить максимальное значение функции
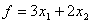
при условиях
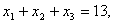
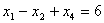 ,
, 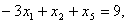
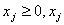 — целые (
— целые (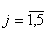 ).
).
Принимая за базисные переменные 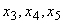 , получим:
, получим:
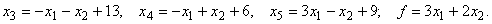
Так как 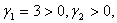 план
план 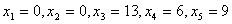 не является оптимальным.
не является оптимальным.
На последнем этапе преобразований по симплекс-методу, последовательно переходя от базисных переменных 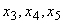 к
к 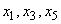 , наконец, к
, наконец, к 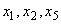 , получим:
, получим:
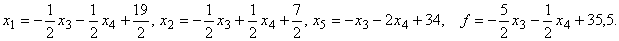
Так как 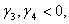 план
план 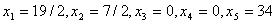 будет оптимальным (
будет оптимальным (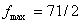 ).
).
Однако найденный оптимальный план не является оптимальным планом решаемой задачи, поскольку две компоненты 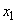 и
и 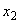 не являются целочисленными. При этом дробные части этих чисел равны между собой. Поэтому для одной из этих переменных составим дополнительное ограничение, например, для переменной
не являются целочисленными. При этом дробные части этих чисел равны между собой. Поэтому для одной из этих переменных составим дополнительное ограничение, например, для переменной 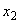 :
:
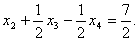
Таким образом, к системе ограничений задачи без учета целочисленности следует добавить неравенство
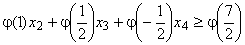 или
или 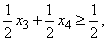
то есть
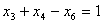 или
или 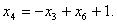
Далее определим максимальное значение функции
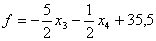
при ограничениях
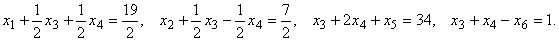
Выберем за базисные переменные 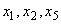 . Получим
. Получим
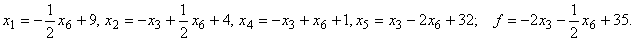
Так как 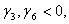 план
план 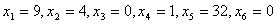 является оптимальным для задачи с введенным дополнительным ограничением. Более того, так как все
является оптимальным для задачи с введенным дополнительным ограничением. Более того, так как все 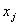 — целые, этот план является оптимальным и для задачи целочисленного программирования.
— целые, этот план является оптимальным и для задачи целочисленного программирования.
При этом плане значение целевой функции равно 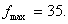
Областью допустимых решений исходной задачи без учета целочисленности является многоугольник ОАВСD (рис.2). Максимальное значение целевая функция принимает в точке С(19/2,7/2); Х=(19/2,7/2,0,0,34) — оптимальный план.
Так как Х=(19/2,7/2,0,0,34) не является оптимальным планом задачи целочисленного программирования (числа 19/2 и 7/2 — дробные), введем дополнительное ограничение 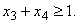 Исключая из него х3 и х4 подстановкой вместо них соответствующих значений из уравнений исходной системы ограничений, получим
Исключая из него х3 и х4 подстановкой вместо них соответствующих значений из уравнений исходной системы ограничений, получим 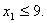 Этому неравенству соответствует полуплоскость, ограниченная прямой
Этому неравенству соответствует полуплоскость, ограниченная прямой 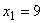 , отсекающей от многоугольника ОАВСD треугольник EFC.
, отсекающей от многоугольника ОАВСD треугольник EFC.
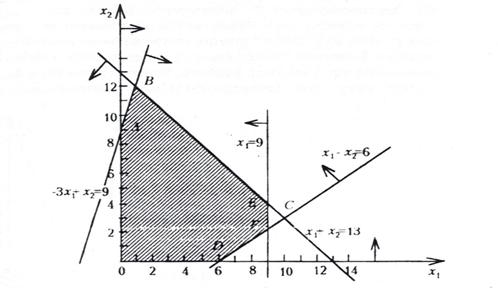
Рис. 2.
Областью допустимых решений полученной исходной задачи является многоугольникOABEFD. Вточке Е(9,4) этого многоугольника целевая функция принимает максимальное значение. Так как координаты точки Е — целые числа и неизвестные 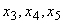 принимают целочисленные значения при подстановке в уравнения значений
принимают целочисленные значения при подстановке в уравнения значений 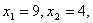 то Х*= (9,4,0,0,32) является оптимальным планом задачи.
то Х*= (9,4,0,0,32) является оптимальным планом задачи.
Приведенные примеры с очевидностью подтверждают эффективность использования методов целочисленного программирования при решении ряда классов технико-экономических задач.
Литература:
1. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
2. Гарькина И. А., Данилов А. М., Жегера К. В. Математическое программирование в управлении качеством материалов / Региональная архитектура и строительство. –2014. –№ 1. –С. 30–36.
3. Гарькина И. А., Данилов А. М., Пылайкин С. А. Из опыта математического моделирования при решении прикладных задач / Альманах современной науки и образования. –2014. –№ 2 (81). — С. 35–37.
4. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
5. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. –2013. — № 5. — С. 42–45.







