Исследуется тригонометрическая система функций, которая получается при решении задачи гашения колебаний балки. Определяется на каком отрезке эта система функций является би-ортогональной.
Ключевые слова: би-ортогональные системы, уравнение колебаний балки, задача гашения.
On bi-orthogonality of the system of functions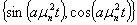 
on the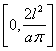 
Atamuratov Andrey Zhienbaevich
MATI — Russian State Technological University of K. E. Tsiolkovsky, Moscow, Postgraduate of Applied Mathematics and Computer Science department
Постановка проблемы. Колебания балки описываются следующим уравнением
, 
,
,
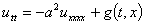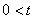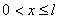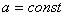(1)
Начальные отклонения и скорость перемещения балки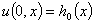 
, 
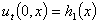, будем рассматривать как начальные условия. На концах балки наложим условия нежёсткого закрепления 
, 
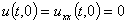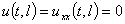. При решении задачи гашения колебаний балки [1–6], которая состоит в том, что требуется найти управляющую функцию 
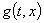из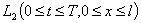 
, позволяющую за минимальное время 
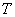перевести балку из возмущённого состояния в состояние покоя 
, 
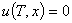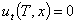, решая её аналитическим способом (Фурье и проблема моментов) [7], мы приходим к следующей системе моментов
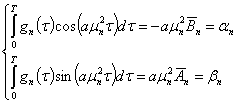, (2)
где собственные числа и коэффициенты Фурье задаются так
,
, 
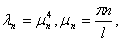
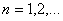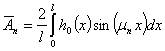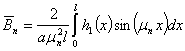. (3)
Дальнейшее же решение полностью зависит от того можем ли мы найти для системы функций 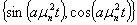би-ортогональную и для какого 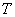, то есть на каком отрезке 
.
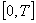Основное определение. Система функций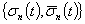 
является би-ортогональной [8] к системе 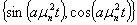на отрезке 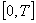, если выполняется следующее
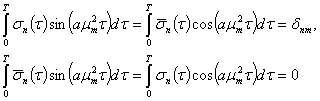(4)
Теорема. Система функций 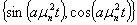на промежутк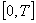е , где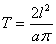 
, является би-ортогональной сама к себе.
Рассмотрим основные соотношения между этими функциями. Пусть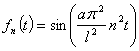
, тогда для некоторого промежутка
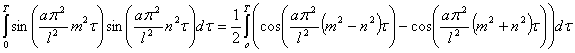
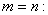
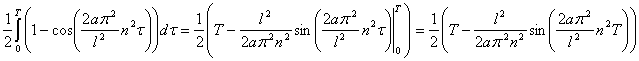
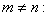
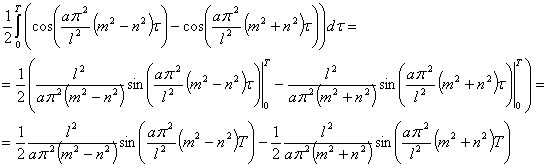
Пусть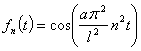 
, тогда
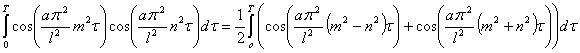
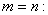
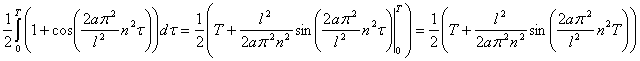
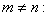
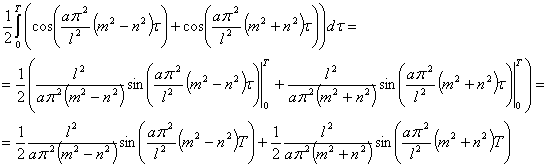
Взаимное соотношение
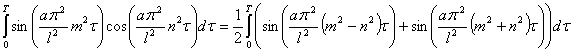
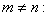
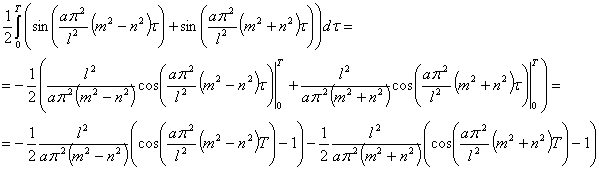
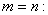
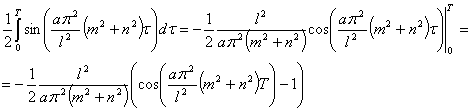
Тогда, если положить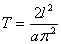 
, то равенства (4) будут выполняться.
Литература:
1. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А.. О гашении колебаний балки. // Труды ИСА РАН. Динамика неоднородных систем. Том 50(1). — М.: Книжный дом «ЛИБРОКОМ», 2010. — С. 53–58.
2. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А. О гашении колебаний сложных механических структур // Авиакосмическая техника и технология, 2012, № 4. С. 54–59.
3. Atamuratov A., Mikhailov I., Muravey L. On the numerical damping of beam's vibrations. VII International Aerospace Congress IAC’12, August 25–31, 2012, Moscow, Russia, Proceedings. Электронный вид. Зарегистрировано в ВГУП НГЦ в ИНФОРМ-РЕГИСТР. Гос. рег. № 0321303652. 2013. C. 103–106.
4. Атамуратов А. Ж. Решение уравнения колебаний балки при шарнирном закреплении на границах. // Молодой ученый. 2014. № 2. С. 1–7. http://www.moluch.ru/archive/61/8996/
5. Атамуратов А. Ж. Численный метод решения уравнения колебаний балки при разных типах граничных условий. // Молодой ученый. 2014. № 2. С. 7–12. http://www.moluch.ru/archive/61/9146/
6. Muravey L., Mikhailov I., Atamuratov A., The damping problem of vibrations for large mechanical systems // ICIAM2011, Abstracts, Vancouver, Canada, July 18–22, 2011. P. 87.
7. Atamuratov A., Mikhailov I., Muravey L. On the numerical damping of beam’s vibrations // VII International Aerospace Congress IAC’12. Abstracts. Moscow, Russia. 26–31 August, 2012. P. 31–32.
8. Атамуратов А. Ж. Приведение к тригонометрической проблеме моментов на примере задачи гашения колебаний прямоугольной мембраны, балки и прямоугольной пластины. // Молодой ученый. № 11. 2013. С. 6–10. http://www.moluch.ru/archive/58/8092/
9. Lagness J. E. Control of wave process with distributed controls supported on a subregion // SIAM Journ. Control and Optim. 1983. Vol. 1, no. 1. Pp. 68–85.
